LeetCode刷题--- 乘积为正数的最长子数组长度-编程知识

LeetCode刷题--- 乘积为正数的最长子数组长度

个人主页：元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客

个人专栏

力扣递归算法题

http://t.csdnimg.cn/yUl2I

【C++】

http://t.csdnimg.cn/6AbpV

数据结构与算法

http://t.csdnimg.cn/hKh2l

前言：这个专栏主要讲述动态规划算法，所以下面题目主要也是这些算法做的

我讲述题目会把讲解部分分为3个部分：
1、题目解析

2、算法原理思路讲解

3、代码实现

乘积为正数的最长子数组长度

题目链接：乘积为正数的最长子数组长度

题目

给你一个整数数组 nums ，请你求出乘积为正数的最长子数组的长度。

一个数组的子数组是由原数组中零个或者更多个连续数字组成的数组。

请你返回乘积为正数的最长子数组长度。

示例 1：

输入：nums = [1,-2,-3,4]
输出：4
解释：数组本身乘积就是正数，值为 24 。

示例 2：

输入：nums = [0,1,-2,-3,-4]
输出：3
解释：最长乘积为正数的子数组为 [1,-2,-3] ，乘积为 6 。
注意，我们不能把 0 也包括到子数组中，因为这样乘积为 0 ，不是正数。

示例 3：

输入：nums = [-1,-2,-3,0,1]
输出：2
解释：乘积为正数的最长子数组是 [-1,-2] 或者 [-2,-3] 。

提示：

1 <= nums.length <= 10^5
-10^9 <= nums[i] <= 10^9

解法

算法原理解析

我们这题使用动态规划，我们做这类题目可以分为以下五个步骤

状态显示
状态转移方程
初始化（防止填表时不越界）
填表顺序
返回值

状态显示

f[i] 表示：以 i 结尾的所有子数组中，乘积为「正数」的最长子数组的长度。

g[i] 表示：以 i 结尾的所有子数组中，乘积为「负数」的最长子数组的长度。

状态转移方程

遍历每⼀个位置的时候，我们要同步更新两个 dp 数组的值。

对于 f[i] ，也就是以 i 为结尾的乘积为「正数」的最⻓⼦数组，根据 nums[i] 的值，可以分为三种情况：

nums[i] = 0 时，所有以 i 为结尾的⼦数组的乘积都不可能是正数，此时 f[i] = 0 ；
nums[i] > 0 时，那么直接找到 f[i - 1] 的值（这⾥请再读⼀遍 f[i - 1] 代表的意义，并且考虑如果 f[i - 1] 的结值是 0 的话，影不影响结果），然后加⼀即可，此时 f[i] = f[i - 1] + 1 ；
nums[i] < 0 时，此时我们要看 g[i - 1] 的值（这⾥请再读⼀遍 g[i - 1] 代表的意义。因为负负得正，如果我们知道以 i - 1 为结尾的乘积为负数的最⻓⼦数组的⻓度，加上 1 即可），根据 g[i - 1] 的值，⼜要分两种情况：
1. g[i - 1] = 0 ，说明以 i - 1 为结尾的乘积为负数的最⻓⼦数组是不存在的，又因为 nums[i] < 0 ，所以以 i 结尾的乘积为正数的最⻓⼦数组也是不存在的，此时 f[i] = 0 ；
2. g[i - 1] != 0 ，说明以 i - 1 为结尾的乘积为负数的最⻓⼦数组是存在的，又因为 nums[i] < 0 ，所以以 i 结尾的乘积为正数的最⻓⼦数组就等于 g[i - 1] + 1 ；

综上所述， nums[i] < 0 时， f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;

同理可得， nums[i] > 0 时，g[i] = g[i-1] == 0 ? 0 : g[i-1] + 1;

初始化（防止填表时不越界）

在本题中，最前⾯加上⼀个格⼦，并且让 f[0] = g[0] = 0 即可。

填表顺序

根据「状态转移⽅程」易得，填表顺序为「从左往右，两个表⼀起填」。

返回值

根据「状态表示」，我们要返回 f 表中的最⼤值。

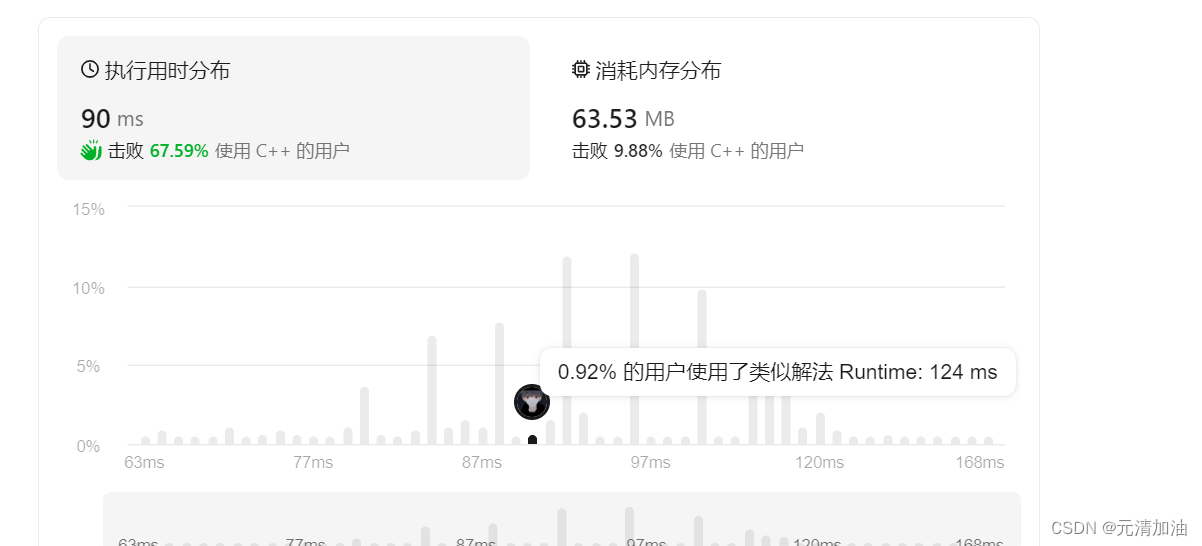
以上本道题目已经讲解完毕，大家可以试一试了。

代码实现

class Solution {
public:int getMaxLen(vector<int>& nums) {int n = nums.size();vector<int> f(n + 1);		// 以i为结尾，乘积为正数的最长子数组vector<int> g(n + 1);		// 以i为结尾，乘积为负数的最长子数组// 初始化f[0] = 0;g[0] = 0;int ans = INT_MIN;for (int i = 1; i <= n; i++){if (nums[i-1] > 0){f[i] = f[i - 1] + 1;g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;}else if (nums[i-1] < 0){f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;g[i] = f[i - 1] + 1;}ans = max(ans, f[i]);}return ans;}
};