文章目录
- 一、图的遍历
- 二、广度优先遍历
- 1.思想
- 2.算法实现
- 3.六度好友
- 三、深度优先遍历
- 1.思想
- 2.代码实现
- 四、其他问题
一、图的遍历
对于图而言,我们的遍历一般是遍历顶点,而不是边,因为边的遍历是比较简单的,就是邻接矩阵或者邻接表里面的内容。而对于遍历顶点就稍微有点麻烦了。
给定一个图G和其中任意一个顶点v0,从v0出发,沿着图中各边访问图中的所有顶点,且每个顶点仅被遍历一次。"遍历"即对结点进行某种操作的意思。
树以前前是怎么遍历的,此处可以直接用来遍历图吗?为什么?
树以前的遍历有深度优先(先序、中序、后序)和广度优先遍历(层序遍历)两种。
图也是类似的。
二、广度优先遍历
1.思想
下面是广度优先遍历的一个比较形象的例子
对于下面的图而言,也是类似的,先去找A,然后去遍历A的周围的三个结点,然后遍历这三个结点的周围结点,一层一层往外遍历,最终遍历完所有的结点,需要注意的是不要重复遍历了!
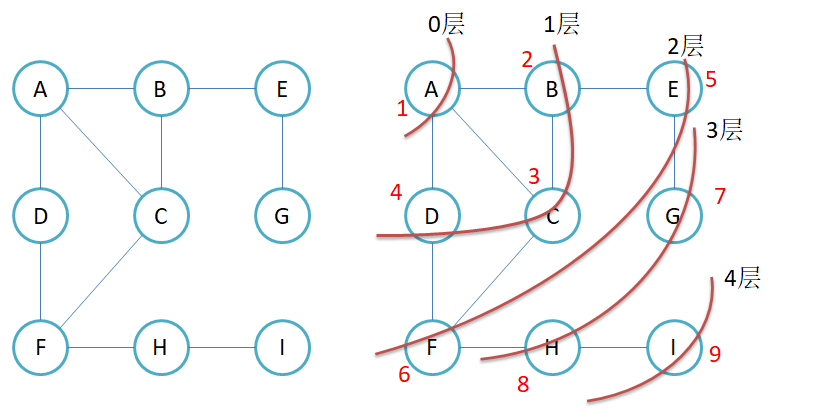
2.算法实现
我们这里用邻接矩阵来实现我们的代码。如下代码所示。
namespace matrix
{//V代表顶点, W是weight代表权值,MAX_W代表权值的最大值,Direction代表是有向图还是无向图,flase表示无向template<class V, class W, W Max_W = INT_MAX, bool Direction = false>class Graph{public://图的创建//1. IO输入 不方便测试//2. 图结构关系写到文件,读取文件//3. 手动添加边Graph(const V* a, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; i++){_vertexs.push_back(a[i]);_indexMap[a[i]] = i;}_matrix.resize(n);for (size_t i = 0; i < _matrix.size(); i++){_matrix[i].resize(n, Max_W);}}size_t GetVertexIndex(const V& v){//return _indexMap[v];auto it = _indexMap.find(v);if (it != _indexMap.end()){return it->second;}else{//assert(false)throw invalid_argument("顶点不存在");return -1;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetVertexIndex(src);size_t dsti = GetVertexIndex(dst);_matrix[srci][dsti] = w;if (Direction == false){_matrix[dsti][srci] = w;}}void Print(){for (size_t i = 0; i < _vertexs.size(); i++){cout << "[" << i << "]" << "->" << _vertexs[i] << endl;}cout << endl;cout << " ";for (int i = 0; i < _vertexs.size(); i++){//cout << _vertexs[i] << " ";printf("%-3d ", i);}cout << endl;for (size_t i = 0; i < _matrix.size(); i++){//cout << _vertexs[i] << " ";printf("%d ", i);for (size_t j = 0; j < _matrix[i].size(); j++){if (_matrix[i][j] == INT_MAX){cout << " * " << " ";}else{printf("%-3d ", _matrix[i][j]);//cout << _matrix[i][j] << " ";}}cout << endl;}}void BFS(const V& src){int srci = GetVertexIndex(src);queue<int> q; //广度遍历的队列vector<bool> visited(_vertexs.size(), false); //标记数组q.push(srci); //起点入队visited[srci] = true; //已经被遍历过了while (!q.empty()){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << endl;//把front顶点的邻接顶点入队列for (size_t i = 0; i < _matrix[front].size(); i++){if (_matrix[front][i] != Max_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}} private:vector<V> _vertexs; //顶点集合map<V, int> _indexMap; //顶点对应的下标关系vector<vector<W>> _matrix; //临界矩阵};
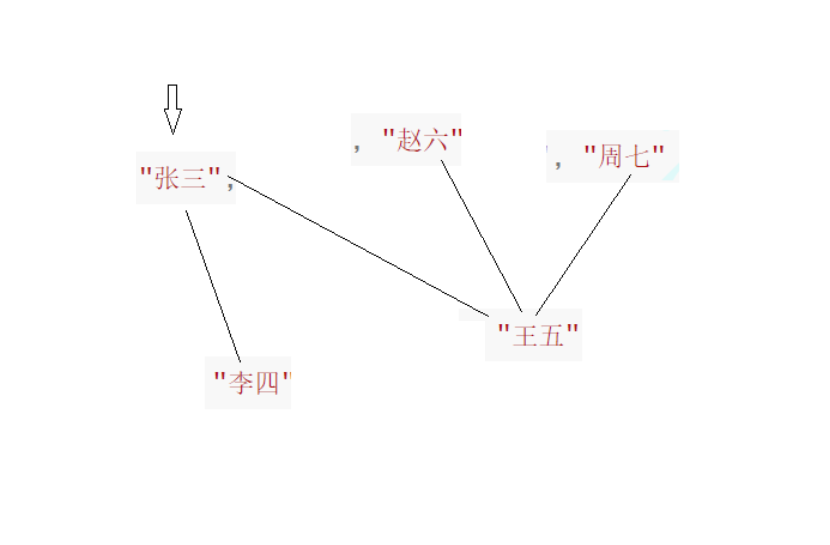
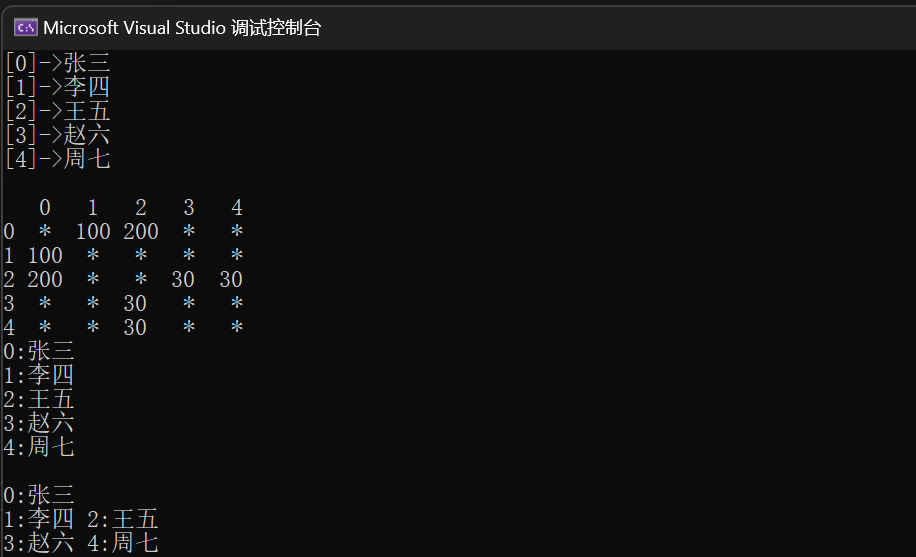
在上面的代码当中,这个图的如下所示
在BFS的时候,我们使用一个队列和一个标记数组来解决。
我们先将第一个起点入队,并且进行标记已经被遍历了,然后像二叉树的层序遍历一样,一层一层去寻找它的周围结点。由于我们用的是邻接矩阵,那么我们就可以以出队列的这个结点为起点,遍历邻接矩阵的对应行,找到满足的进行入队列,然后依次进行标记。从而最终可以遍历整个图
最终结果为
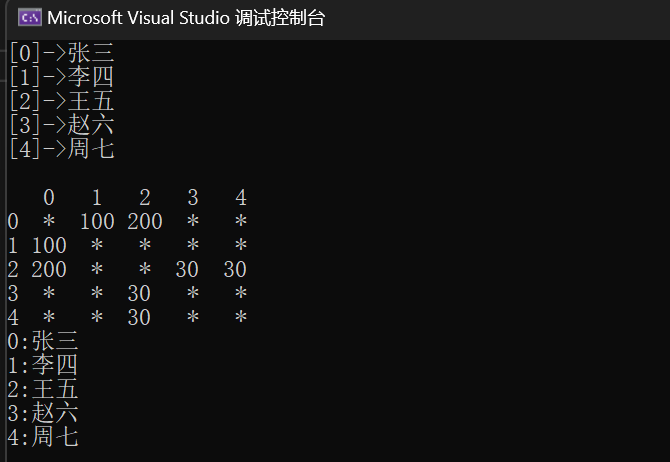
3.六度好友
如下面的题目就是一个简单的广度优先遍历
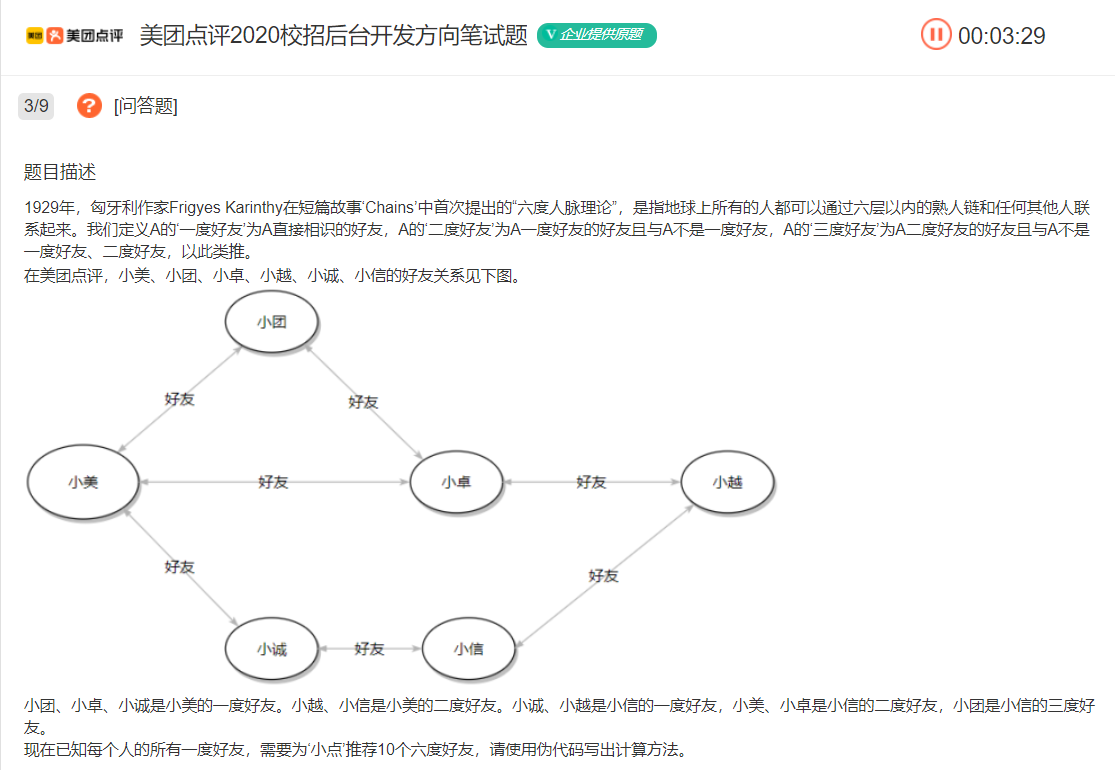
这道题与二叉树中求出第几层的元素是十分类似的。就是层序遍历,不过要打印出第六层的结果
void BFSLevel(const V& src)
{int srci = GetVertexIndex(src);queue<int> q; //广度遍历的队列vector<bool> visited(_vertexs.size(), false); //标记数组q.push(srci); //起点入队visited[srci] = true; //已经被遍历过了int levelSize = 1;while (!q.empty()){for (int i = 0; i < levelSize; i++){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << " ";//把front顶点的邻接顶点入队列for (size_t i = 0; i < _matrix[front].size(); i++){if (_matrix[front][i] != Max_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}cout << endl;levelSize = q.size();}
}
void TestGraphBDFS()
{string a[] = { "张三", "李四", "王五", "赵六", "周七" };Graph<string, int> g1(a, sizeof(a) / sizeof(string));g1.AddEdge("张三", "李四", 100);g1.AddEdge("张三", "王五", 200);g1.AddEdge("王五", "赵六", 30);g1.AddEdge("王五", "周七", 30);g1.Print();g1.BFS("张三");cout << endl;g1.BFSLevel("张三");
}
这里我们用一个循环来记录每层的个数,每打印够一层就换行。如上代码所示
运行结果为
三、深度优先遍历
1.思想

如上是深度优先的一个形象的案例,下面是深度优先在一个图中的实际场景
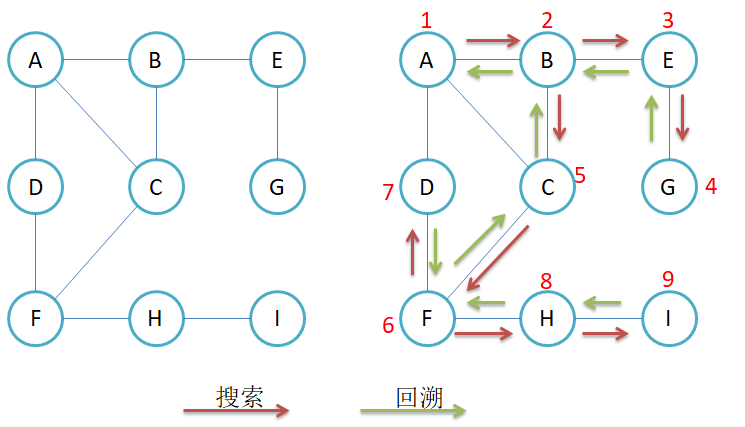
我们可以看到,他就像二叉树的先序遍历一样,一直走到最深层,然后退回去。这里需要注意的就是要进行标记已经遍历过的结点
2.代码实现
如下是深度优先的代码实现
namespace matrix
{//V代表顶点, W是weight代表权值,MAX_W代表权值的最大值,Direction代表是有向图还是无向图,flase表示无向template<class V, class W, W Max_W = INT_MAX, bool Direction = false>class Graph{public://图的创建//1. IO输入 不方便测试//2. 图结构关系写到文件,读取文件//3. 手动添加边Graph(const V* a, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; i++){_vertexs.push_back(a[i]);_indexMap[a[i]] = i;}_matrix.resize(n);for (size_t i = 0; i < _matrix.size(); i++){_matrix[i].resize(n, Max_W);}}size_t GetVertexIndex(const V& v){//return _indexMap[v];auto it = _indexMap.find(v);if (it != _indexMap.end()){return it->second;}else{//assert(false)throw invalid_argument("顶点不存在");return -1;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetVertexIndex(src);size_t dsti = GetVertexIndex(dst);_matrix[srci][dsti] = w;if (Direction == false){_matrix[dsti][srci] = w;}}void Print(){for (size_t i = 0; i < _vertexs.size(); i++){cout << "[" << i << "]" << "->" << _vertexs[i] << endl;}cout << endl;cout << " ";for (int i = 0; i < _vertexs.size(); i++){//cout << _vertexs[i] << " ";printf("%-3d ", i);}cout << endl;for (size_t i = 0; i < _matrix.size(); i++){//cout << _vertexs[i] << " ";printf("%d ", i);for (size_t j = 0; j < _matrix[i].size(); j++){if (_matrix[i][j] == INT_MAX){cout << " * " << " ";}else{printf("%-3d ", _matrix[i][j]);//cout << _matrix[i][j] << " ";}}cout << endl;}}void BFS(const V& src){int srci = GetVertexIndex(src);queue<int> q; //广度遍历的队列vector<bool> visited(_vertexs.size(), false); //标记数组q.push(srci); //起点入队visited[srci] = true; //已经被遍历过了while (!q.empty()){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << endl;//把front顶点的邻接顶点入队列for (size_t i = 0; i < _matrix[front].size(); i++){if (_matrix[front][i] != Max_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}} void BFSLevel(const V& src){int srci = GetVertexIndex(src);queue<int> q; //广度遍历的队列vector<bool> visited(_vertexs.size(), false); //标记数组q.push(srci); //起点入队visited[srci] = true; //已经被遍历过了int levelSize = 1;while (!q.empty()){for (int i = 0; i < levelSize; i++){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << " ";//把front顶点的邻接顶点入队列for (size_t i = 0; i < _matrix[front].size(); i++){if (_matrix[front][i] != Max_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}cout << endl;levelSize = q.size();}}void _DFS(size_t srci, vector<bool>& visited){cout << srci << ":" << _vertexs[srci] << endl;visited[srci] = true;for (int i = 0; i < _matrix[srci].size(); i++){if (_matrix[srci][i] != Max_W && visited[i] == false){_DFS(i, visited);}}}void DFS(const V& src){int srci = GetVertexIndex(src);vector<bool> visited(_vertexs.size(), false);_DFS(srci, visited);}private:vector<V> _vertexs; //顶点集合map<V, int> _indexMap; //顶点对应的下标关系vector<vector<W>> _matrix; //临界矩阵};void TestGraph(){Graph<char, int, INT_MAX, true> g("0123", 4);g.AddEdge('0', '1', 1);g.AddEdge('0', '3', 4);g.AddEdge('1', '3', 2);g.AddEdge('1', '2', 9);g.AddEdge('2', '3', 8);g.AddEdge('2', '1', 5);g.AddEdge('2', '0', 3);g.AddEdge('3', '2', 6);g.Print();}void TestGraphBDFS(){string a[] = { "张三", "李四", "王五", "赵六", "周七" };Graph<string, int> g1(a, sizeof(a) / sizeof(string));g1.AddEdge("张三", "李四", 100);g1.AddEdge("张三", "王五", 200);g1.AddEdge("王五", "赵六", 30);g1.AddEdge("王五", "周七", 30);g1.Print();g1.BFS("张三");cout << endl;g1.BFSLevel("张三");cout << endl;g1.DFS("张三");}}
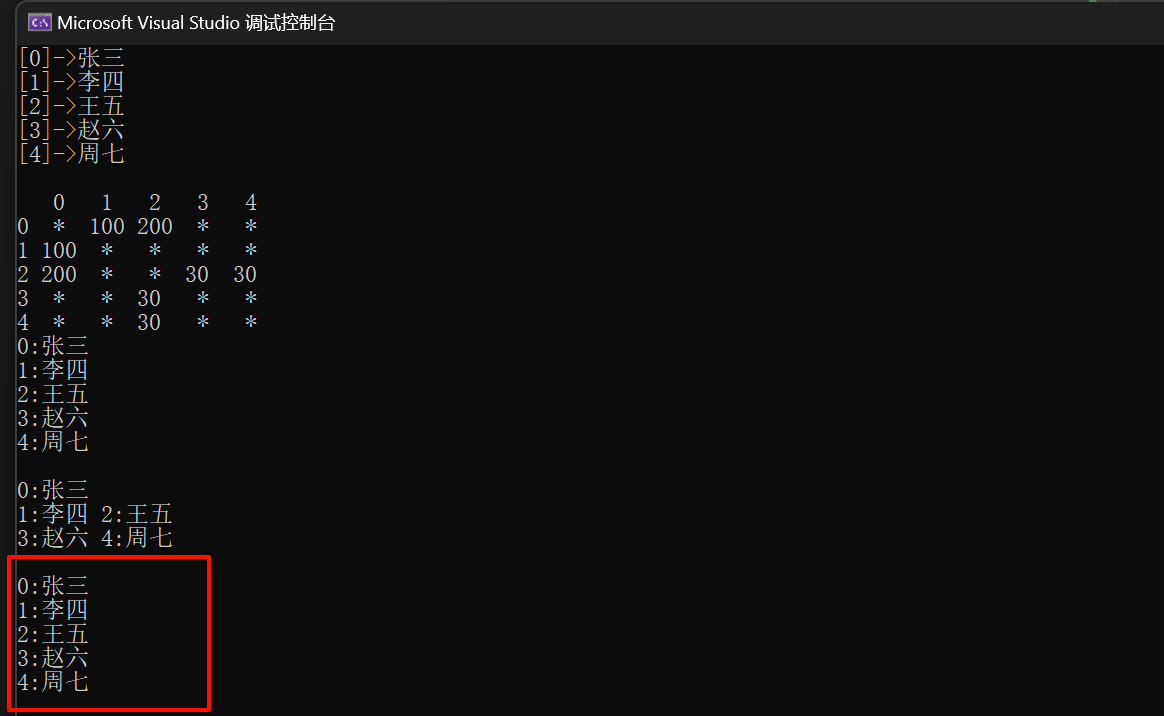
像先序遍历一样,这里也是需要一个子函数比较好的,因为我们需要使用递归,让子函数去进行递归是最好的
运行结果如下所示
四、其他问题
关于深度优先和广度优先,上面的清空自然是很理想的情况。并且由于起点不同,深度优先和广度优先的结果是不同的。但是有时候,也会出现下面的问题。
比如图不连通的问题。也就是图存在孤立的结点。那么这样的话,以某个点为起点就没有遍历完成
这里我们可以有个解决方案是从visited数组中寻找没有遍历的结点,在进行一次深度优先或者广度优先。也就是要在原来的代码上在套一层。