目录
- 一. 多分类问题解决策略
- 1. 一对一策略 OVO (One-vs-One)
- 2. 一对剩余策略 OVR(One-vs-Rest)
- 二. Softmax回归算法
【前景回顾】
这里我们先来总结Logistic回归算法:
模型函数 p = s i g m o i d ( w x + b ) p = sigmoid(wx+b) p=sigmoid(wx+b)
函数解释:Logistic回归不仅可以解决线性分类问题,对于非线性分类问题也可以解决,即通过多项式扩展方式
目标函数 l o s s = − y l n ( p ) − ( 1 − y ) l n ( 1 − p ) loss = -yln(p)-(1-y)ln(1-p) loss=−yln(p)−(1−y)ln(1−p)
其中,对于参数
{ ω ′ = ω − α ∂ l o s s ∂ w b ′ = b − α ∂ l o s s ∂ b \left\{\begin{matrix}{\omega}'= \omega-\alpha \frac{\partial loss}{\partial w} \\\\{b}'= b-\alpha \frac{\partial loss}{\partial b} \end{matrix}\right. ⎩ ⎨ ⎧ω′=ω−α∂w∂lossb′=b−α∂b∂loss
前面我们在文章中讨论了二分类问题,下面我们来讨论多分类问题
一. 多分类问题解决策略
对于有多个类别的样本,我们常采用的策略是:
1. 一对一策略 OVO (One-vs-One)
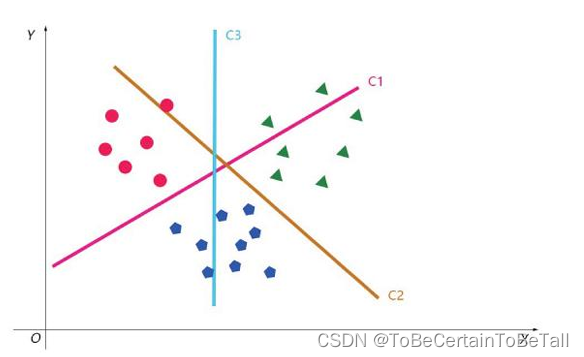
假设我们现在有A、B、C三类做法:1. 取A和B,用二分类方法对其进行分类取A和C,用二分类方法对其进行分类取B和C,用二分类方法对其进行分类2. 进行上述操作后,得到三个分类器,即C1,C2,C33. 对于新进样本,根据投票或者概率最大者来确定最终的类别
构造分类器个数: k ( k − 1 ) / 2 ,其中 k 为类别个数 k(k-1)/2,其中k为类别个数 k(k−1)/2,其中k为类别个数
2. 一对剩余策略 OVR(One-vs-Rest)
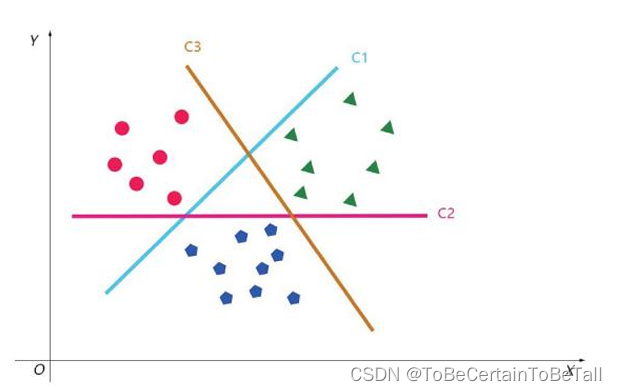
假设我们现在有A、B、C三类做法:1. 取A和B、C,用二分类方法对其进行分类取B和A、C,用二分类方法对其进行分类取C和A、B,用二分类方法对其进行分类2. 进行上述操作后,得到三个分类器,即C1,C2,C33. 对于新进样本,用得到的分类器一一进行判断,根据概率最大来确定最终的类别
二. Softmax回归算法
对于上面提到的两种多分类策略,在对某个新数据预测时,都存在一个缺点:
C个分类器预测得到的C个概率之和不等于1
即:关于某个样本类别,在C个分类器下的预测值无相关性
针对上面的问题,Softmax回归算法能很好解决这个问题
假设我们采集到数据后,进行标注,得到数据集如下:
x 1 ( i ) , x 2 ( i ) , . . . , x N ( i ) , y ( i ) x_{1}^{(i)}, x_{2}^{(i)}, ... , x_{N}^{(i)}, y^{(i)} x1(i),x2(i),...,xN(i),y(i)
其中,数据集的A分类标记为 y ( i ) = 0 y^{(i)}=0 y(i)=0
数据集的B分类标记为 y ( i ) = 1 y^{(i)}=1 y(i)=1
数据集的C分类标记为 y ( i ) = 2 y^{(i)}=2 y(i)=2
数据集的D分类标记为 y ( i ) = 3 y^{(i)}=3 y(i)=3
…
对于共有C个类别的分类问题,我们可以采用上述OVR策略得到C个分类器,并用距离d来衡量某个样本属于某类的可能:
d = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ N x N ,其中 d 的取值为 ( − ∞ , + ∞ ) d = \theta _{0}+ \theta _{1}x_{1}+\theta _{2}x_{2}+ ... +\theta _{N}x_{N},其中d的取值为(-∞,+∞) d=θ0+θ1x1+θ2x2+...+θNxN,其中d的取值为(−∞,+∞)
这里需要重点理解下d的具体含义:
以三分类OVR策略为例子,就得到了三个分类器假设我们得到分类器C1:
C1:区分A类和B、C类的决策边界
假设我们用C1作为分类器:
对新输入数据进行判定时,相当于对该样本点做C1分类器的垂线,即上述式子d
请注意,这个d值判定的是该样本点属于A类的概率
这一点与Logistic函数是类似的
计算的 h θ ( x ) h_{\theta } (x) hθ(x)结果是以正样本为依据
即所计算的样本属于 正样本/正类 的概率
我们定义Softmax函数为
S = e i ∑ e i S = \frac{e^{i} }{\sum e^{i} } S=∑eiei
将d带入Softmax函数,即
h θ ( x ) = S ( d ( θ ) ) = S ( θ 0 + θ 1 x 1 + θ 2 x 2 + . . . ) h_{\theta } (x) = S(d(\theta ))= S(\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+... ) hθ(x)=S(d(θ))=S(θ0+θ1x1+θ2x2+...)
对于OVR策略下的多分类而言,我们得到x属于y时的概率为:
P ( y ∣ x ; θ ) = h θ ( x ) y ( i ) P(y|x;\theta ) = h_{\theta } (x)^{y^{(i)} } P(y∣x;θ)=hθ(x)y(i)
这样我们就可以得到似然函数
L ( θ ) = ∏ i = 1 M h θ ( x ( i ) ) y ( i ) L(\theta)=\prod_{i=1}^{M} h_{\theta }(x^{(i)} )^{y^{(i)} } L(θ)=i=1∏Mhθ(x(i))y(i)
接下来,我们对似然函数求对数,得到公式
l ( θ ) = l n [ L ( θ ) ] = ∑ i = 1 M y ( i ) l n [ h θ ( x ( i ) ) ] l(\theta )=ln\left [ L(\theta)\right ]=\sum_{i=1}^{M}y^{(i)}ln[h_{\theta}(x^{(i)} )] l(θ)=ln[L(θ)]=i=1∑My(i)ln[hθ(x(i))]
结合我们对Logistic回归函数的讲解,softmax回归的损失函数就可以定义为:
J ( θ ) = − l ( θ ) = ∑ i = 1 M − y ( i ) l n [ h θ ( x ( i ) ) ] J(\theta)=-l(\theta)=\sum_{i=1}^{M} -y^{(i)}ln[h_{\theta}(x^{(i)} )] J(θ)=−l(θ)=i=1∑M−y(i)ln[hθ(x(i))]
下面,我们来求解梯度:
在开始推导前,我们为了好描述,对参数做以下解释:
若我们有三个分类器:C1:假定判定猫和其他类,d是关于 β \beta β的一套参数
C2:假定判定狗和其他类,d是关于 α \alpha α的一套参数
C3:假定判定鸟和其他类,d是关于 γ \gamma γ的一套参数假设想用分类器判断样本点是猫的概率(且样本点标签值为:猫)
e z i e^{_z{i} } ezi: 样本点在每个分类器上的预测值,注意每个分类器相关参数不同
∑ k = 1 m e z k {\textstyle \sum_{k=1}^{m}} e^{z_{k} } ∑k=1mezk:样本点在三个分类器上的预测总值对于二分类而言,样本类别非A即B
对于多分类而言,样本类别有很多种选择但每种选择都包含了我们的目标类
即分母总是A+B+C
∂ J ( θ ) ∂ θ j = − y ( i ) h θ ( x ) \frac{\partial J(\theta )}{\partial \theta _{j} }=-\frac{y^{(i)} }{h_{\theta }(x) } ∂θj∂J(θ)=−hθ(x)y(i)
这里为了好描述,我们将h关于 θ \theta θ的函数转换为h关于z的函数
当 i = y i=y i=y :
∂ h j ∂ z i = ∂ ( e z i ∑ k e z k ) ∂ z i \frac{\partial h_{j} }{\partial z_{i} }=\frac{\partial (\frac{e^{z_{i}}}{ {\textstyle \sum_{k}^{}e^{z_{k}}}})}{\partial z_{i} } ∂zi∂hj=∂zi∂(∑kezkezi)
= e z i ∗ ∑ k e z k − e z i ∗ e z i ( ∑ k e z k ) 2 =\frac{e^{z_{i}}\ast{{\textstyle \sum_{k}^{}e^{z_{k}}}}- e^{z_{i}}\ast e^{z_{i}}}{({{\textstyle \sum_{k}^{}e^{z_{k}}}})^{2}} =(∑kezk)2ezi∗∑kezk−ezi∗ezi
= e z i ∑ k e z k ∗ ∑ k e z k − e z i ∑ k e z k =\frac{e^{z_{i}}}{{ {\textstyle \sum_{k}^{}e^{z_{k}}}}} \ast \frac{{\textstyle \sum_{k}^{}e^{z_{k}}}-e^{z_{i}}}{{ {\textstyle \sum_{k}^{}e^{z_{k}}}}} =∑kezkezi∗∑kezk∑kezk−ezi
= e z i ∑ k e z k ∗ ( 1 − e z i ∑ k e z k ) =\frac{e^{z_{i}}}{{ {\textstyle \sum_{k}^{}e^{z_{k}}}}} \ast (1-\frac{e^{z_{i}}}{{{ {\textstyle \sum_{k}^{}e^{z_{k}}}}} } ) =∑kezkezi∗(1−∑kezkezi)
= h i ∗ ( 1 − h i ) =h_{i}\ast (1-h_{i}) =hi∗(1−hi)
当 i ≠ y i\ne y i=y :
∂ h j ∂ z i = ∂ ( e z i ∑ k e z k ) ∂ z i \frac{\partial h_{j} }{\partial z_{i} }=\frac{\partial (\frac{e^{z_{i}}}{ {\textstyle \sum_{k}^{}e^{z_{k}}}})}{\partial z_{i} } ∂zi∂hj=∂zi∂(∑kezkezi)
= 0 ∗ ∑ k e z k − e z j ∗ e z i ( ∑ k e z k ) 2 =\frac{0\ast { {\textstyle \sum_{k}^{}e^{z_{k}}}}-e^{z_{j} }\ast e^{z_{i} } }{({ {\textstyle \sum_{k}^{}e^{z_{k}}})}^{2} } =(∑kezk)20∗∑kezk−ezj∗ezi
= − e z j ∑ k e z k ∗ e z i ∑ k e z k =-\frac{e^{z_{j}}}{{ {\textstyle \sum_{k}^{}e^{z_{k}}}}}\ast \frac{e^{z_{i}}}{{ {\textstyle \sum_{k}^{}e^{z_{k}}}}} =−∑kezkezj∗∑kezkezi
= − h j h i =-h_{j}h_{i} =−hjhi
即,梯度值为:
∂ J ( θ ) ∂ θ j = ∑ i = j ∂ J j ∂ h j ∂ h j ∂ z i + ∑ i ≠ j ∂ J j ∂ h j ∂ h j ∂ z i \frac{\partial J(\theta )}{\partial \theta _{j} }=\sum_{i=j}\frac{\partial J_{j} }{\partial h_{j} }\frac{\partial h_{j} }{\partial z_{i} } +\sum_{i\ne j}\frac{\partial J_{j} }{\partial h_{j} }\frac{\partial h_{j} }{\partial z_{i} } ∂θj∂J(θ)=∑i=j∂hj∂Jj∂zi∂hj+∑i=j∂hj∂Jj∂zi∂hj
= − y i h i ∗ h i ∗ ( 1 − h i ) + ∑ i ≠ j − y j h j ∗ ( − h j h i ) =-\frac{y_{i}}{h_{i} }\ast h_{i}\ast (1-h_{i}) +\sum_{i\ne j}-\frac{y_{j}}{h_{j} }\ast(-h_{j}h_{i}) =−hiyi∗hi∗(1−hi)+∑i=j−hjyj∗(−hjhi)
= h i ∑ j y j − y i =h_{i}\sum_{j}y_{j}-y_{i} =hi∑jyj−yi
感谢阅读🌼
如果喜欢这篇文章,记得点赞👍和转发🔄哦!
有任何想法或问题,欢迎留言交流💬,我们下次见!
本文相关代码存放位置
【Logictic回归代码实现】
祝愉快🌟!