目录
- 一. 损失函数
- 1. 交叉熵损失函数
- 2. 梯度下降
一. 损失函数
Logistic回归算法公式推导篇中,我们通过对似然函数求对数,得到 l ( θ ) l(\theta ) l(θ):
l ( θ ) = l n [ L ( θ ) ] = ∑ i = 1 M { y ( i ) l n [ h θ ( x ( i ) ) ] + ( 1 − y ( i ) ) l n [ 1 − h θ ( x ( i ) ) ] } l(\theta )=ln\left [ L(\theta)\right ]=\sum_{i=1}^{M}\left \{y^{(i)}ln[h_{\theta}(x^{(i)} )]+(1-y^{(i)})ln[1-h_{\theta}(x^{(i)} )] \right \} l(θ)=ln[L(θ)]=i=1∑M{y(i)ln[hθ(x(i))]+(1−y(i))ln[1−hθ(x(i))]}
公式解释1: l ( θ ) l(\theta ) l(θ)
对于似然函数,其含义可以解释为:用已知的观测数据(x值、y值),在某个事件发生概率最大时候,求函数的参数
究竟上述的这个事件发生概率有多大呢?当然是概率越接近1越好,越大越好
结合对似然函数的描述,当似然函数取最大时,模型最优,那么此时我们就可以定义损失函数:
J ( θ ) = − l ( θ ) = ∑ i = 1 M { − y ( i ) l n [ h θ ( x ( i ) ) ] − ( 1 − y ( i ) ) l n [ 1 − h θ ( x ( i ) ) ] } J(\theta)=-l(\theta)=\sum_{i=1}^{M}\left \{-y^{(i)}ln[h_{\theta}(x^{(i)} )]-(1-y^{(i)})ln[1-h_{\theta}(x^{(i)} )] \right \} J(θ)=−l(θ)=i=1∑M{−y(i)ln[hθ(x(i))]−(1−y(i))ln[1−hθ(x(i))]}
公式解释2: J ( θ ) J(\theta ) J(θ)
对于损失函数这样定义不太理解的同学,看这里!!!
明确我们预测的目的:对于一个样本的预测,我们希望模型能预测真实标签的概率越接近1越好,预测的越准确越好
上述目的如果套用至似然函数中,我们就可以说:
对于观测数据(有1有0),我希望模型预测真实标签的概率越接近1越好
若我对似然函数取反,他的含义就变得非常符合我们对于损失函数的要求,即损失越小越好:
对于观测数据,此时我们的期望就变成了,预测真实标签的概率越接近0越好,预测的准确率越低越好;
而事件(预测的准确率越低越好)发生的概率,从预测目的来说,我们希望越低越好,即损失函数越小越好其实,从数学层面讲,似然函数求最大值就等价于求公式前加负号的最小值
1. 交叉熵损失函数
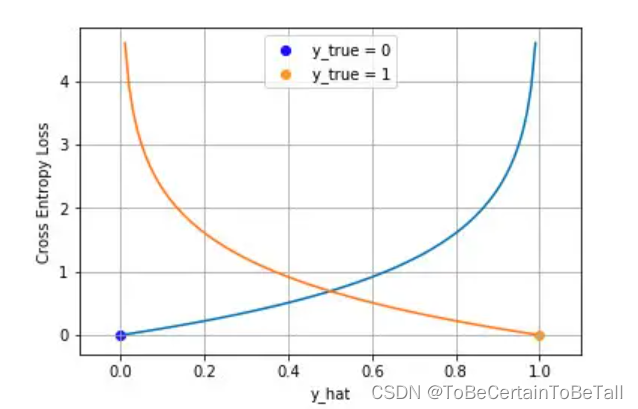
上述定义的损失函数,是非常著名的交叉熵(CrossEntropy)损失函数 ,该函数为凸函数,表示为:
C o s t ( h θ ( x ) , y ) = { − l n ( h θ ( x ) ) , y = 1 − l n ( 1 − h θ ( x ) ) , y = 0 Cost(h_{\theta}(x),y)=\left\{\begin{matrix}-ln(h_{\theta}(x)),y=1 \\-ln(1-h_{\theta}(x)),y=0\end{matrix}\right. Cost(hθ(x),y)={−ln(hθ(x)),y=1−ln(1−hθ(x)),y=0
2. 梯度下降
在定义模型的损失函数后,通过对损失求导来更新梯度,梯度更新公式:
θ i ′ = θ i − α ∂ J ∂ θ i {\theta _{i} }' =\theta _{i}-\alpha \tfrac{\partial J}{\partial \theta _{i}} θi′=θi−α∂θi∂J
其中,损失函数的梯度值为 ∂ J ( θ ) ∂ θ j = ∑ i = 1 M [ h θ ( x ( i ) ) − y ( i ) ] ∗ x j ( i ) \frac{\partial J(\theta )}{\partial \theta _{j} }=\sum_{i=1}^{M}[h_{\theta}(x^{(i)} )-y^{(i)} ] \ast x_{j}^{(i)} ∂θj∂J(θ)=i=1∑M[hθ(x(i))−y(i)]∗xj(i)
推导过程在Logistic回归算法 公式推导篇中
感谢阅读🌼
如果喜欢这篇文章,记得点赞👍和转发🔄哦!
有任何想法或问题,欢迎留言交流💬,我们下次见!
祝愉快🌟!