低密度奇偶校验码LDPC（七）——SPA和积译码算法的简化-编程知识

低密度奇偶校验码LDPC（七）——SPA和积译码算法的简化

一、SPA译码算法的实际应用

查找表与拟合

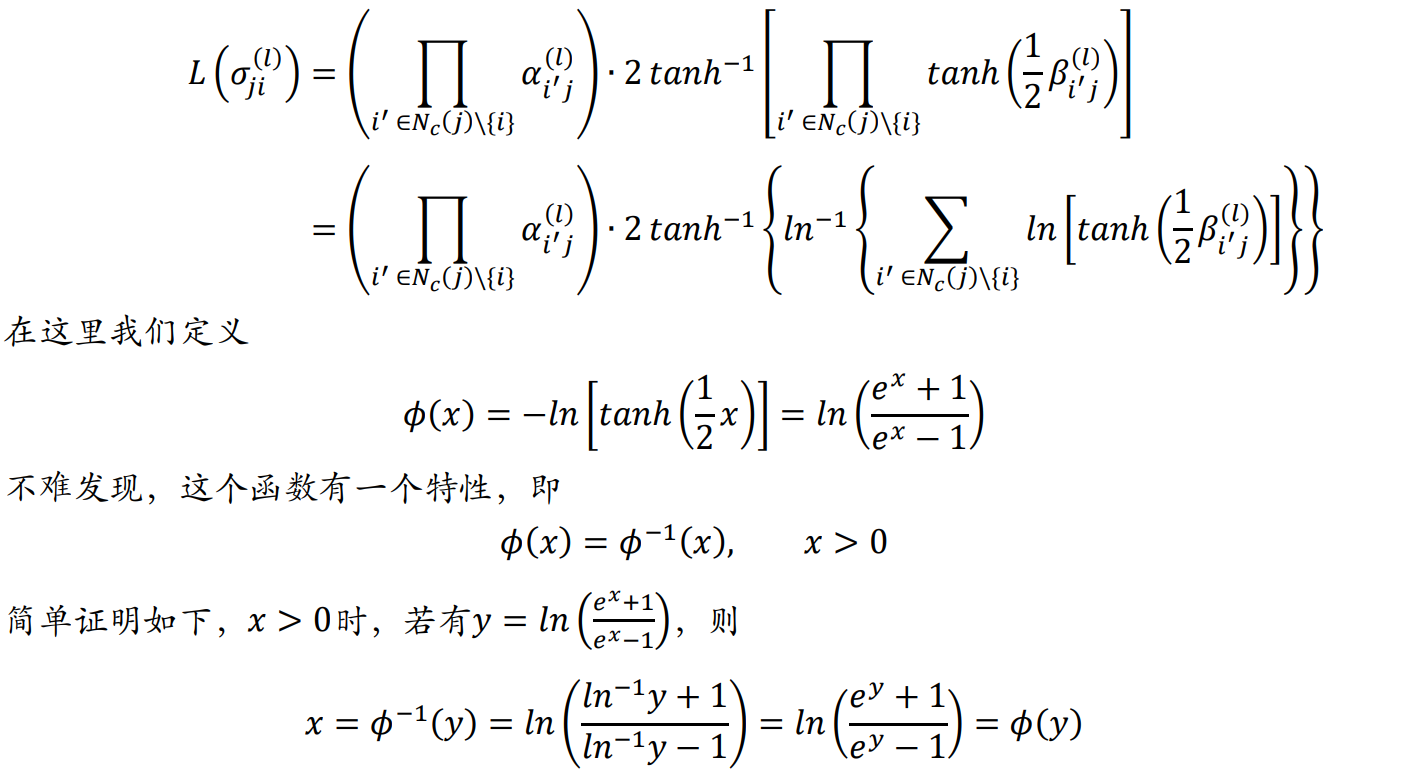
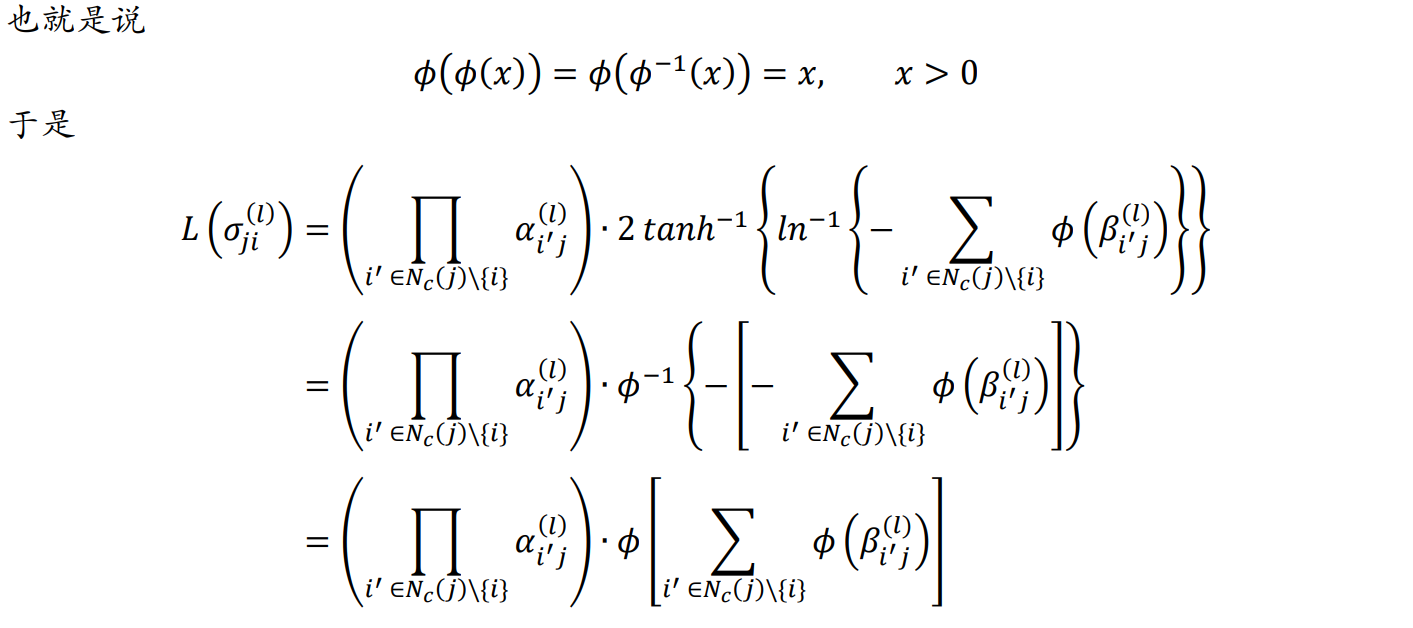
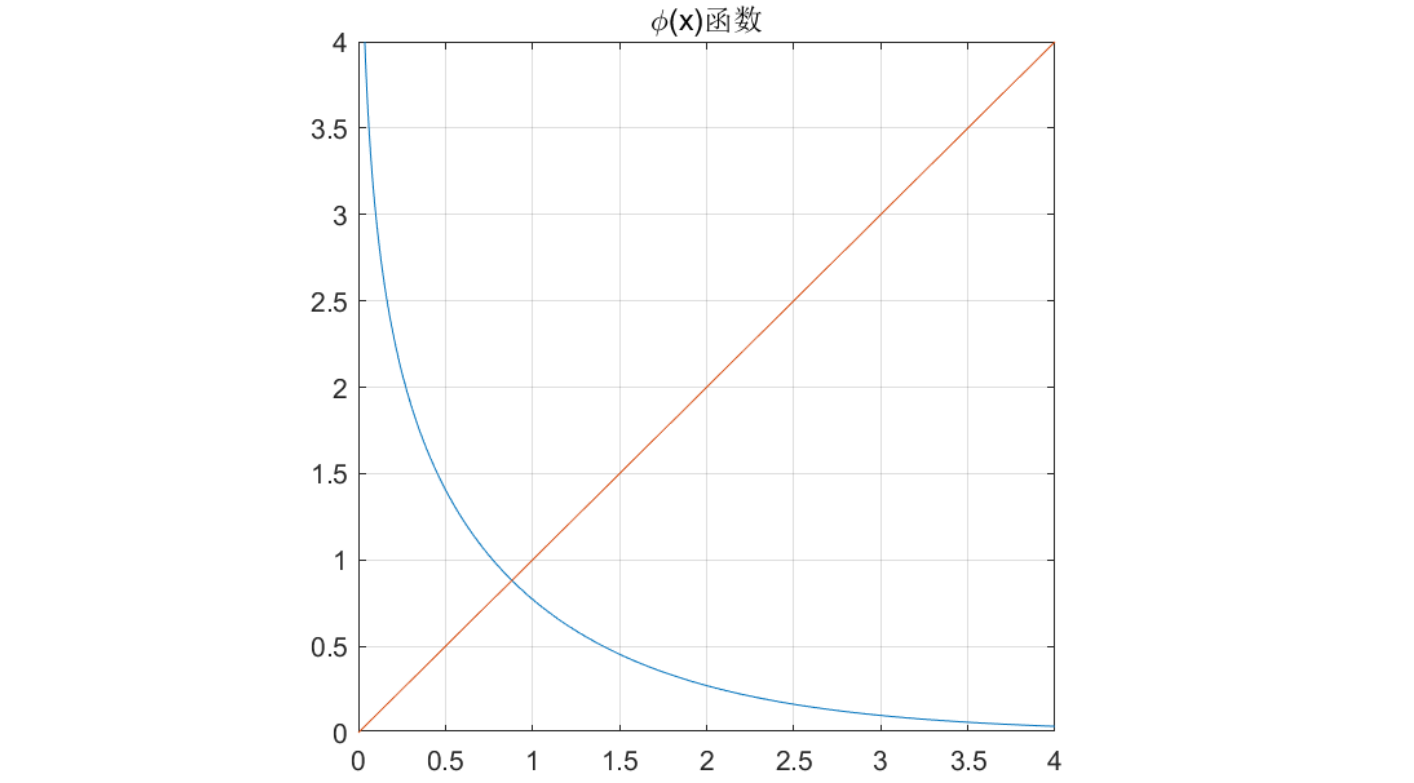
盒加SPA译码器

二、SPA译码算法的简化算法

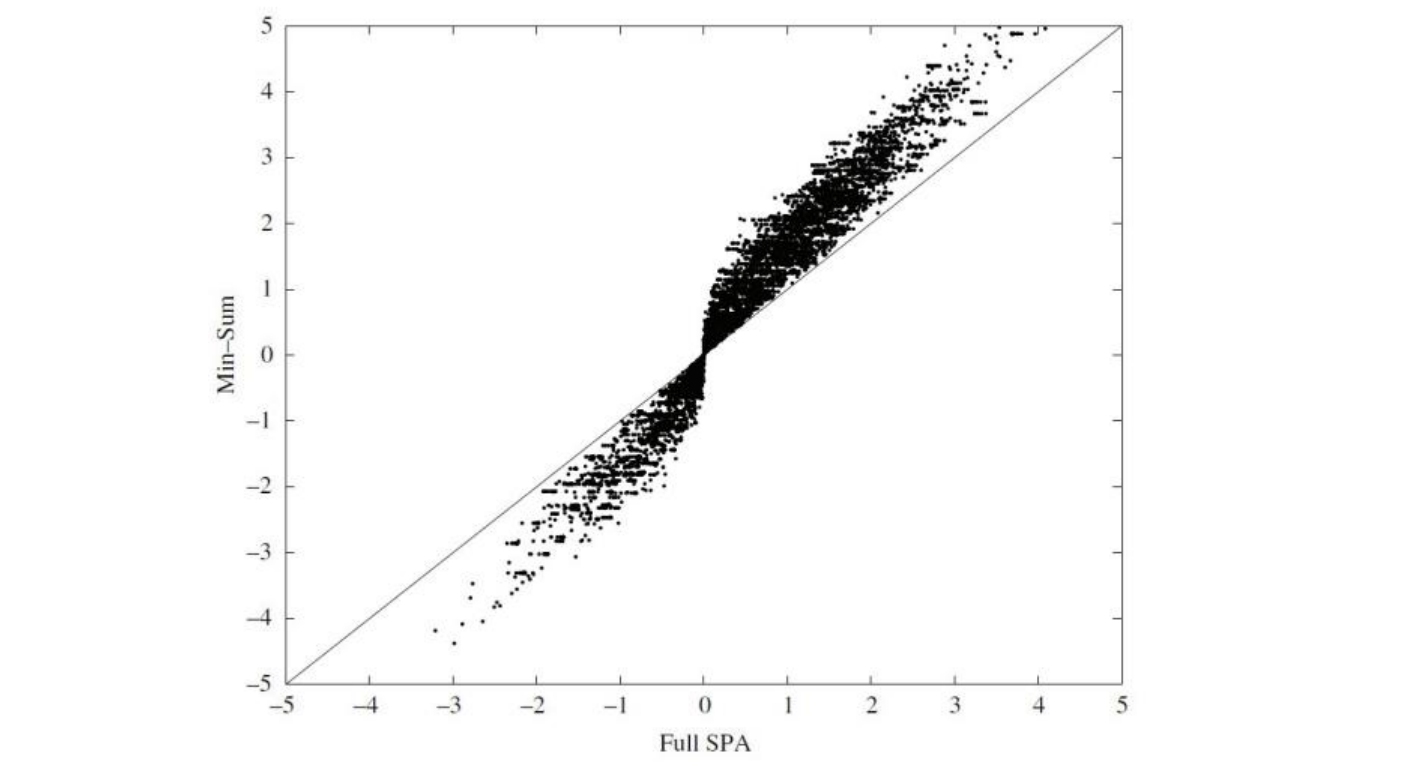
最小和算法(MSA)

归一化最小和算法(Normalized MSA, NMSA)

偏移最小和算法(Offset MSA, OMSA)

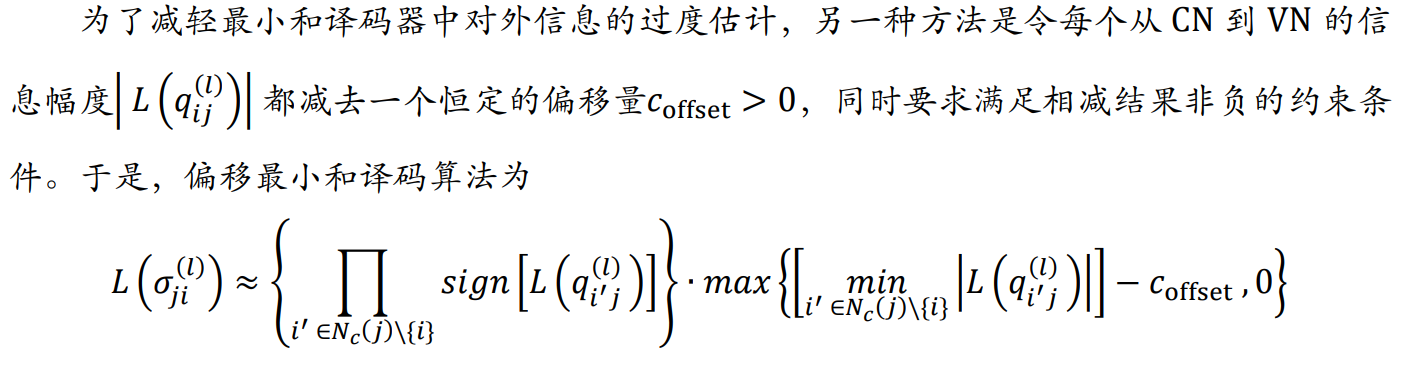
三、NMSA算法的Matlab实现

function [x_hat, iter_this_time] = Layered_NMSA_BP_decoder(llr, H_row_one_absolute_index, H_comlumn_one_relative_index, N, M, vn_degree, cn_degree, max_iter,alfa)
VN_array = zeros(max(vn_degree), N);
CN_tanh_tmp = zeros(max(cn_degree), 1);%CN temporary memory.
iter_this_time = max_iter;
for t = 1 : max_iterfor c = 1 : Mproduct = 1;for c_neighbor = 1 : cn_degree(c)%read data from VNs, and then store in CNs memory.Lji = sum(VN_array(:, H_row_one_absolute_index(c, c_neighbor))) + llr(H_row_one_absolute_index(c, c_neighbor)) - VN_array(H_comlumn_one_relative_index(c, c_neighbor), H_row_one_absolute_index(c, c_neighbor));%VN update. However, this simple MATLAB sentence consumes a lot of time.%CN_tanh_tmp(c_neighbor) = 1 - 2/(1 + exp(Lji));%Exact decoding. Equivalent to tanh(x/2), usually faster.if Lji==0Lji=1e-15;endCN_tanh_tmp(c_neighbor) =Lji;product = product * sign(Lji);%Avoid repeated calculations.endfor c_neighbor = 1 : cn_degree(c)Lij = product/sign(CN_tanh_tmp(c_neighbor));%Extract Extrinsic information, i.e., divide itself.minsort=sort(abs(CN_tanh_tmp(1:cn_degree(c))));if abs(CN_tanh_tmp(c_neighbor))==minsort(1)VN_array(H_comlumn_one_relative_index(c, c_neighbor), H_row_one_absolute_index(c, c_neighbor)) = alfa*Lij*max(minsort(2),1e-15);elseVN_array(H_comlumn_one_relative_index(c, c_neighbor), H_row_one_absolute_index(c, c_neighbor)) = alfa*Lij*max(minsort(1),1e-15);endendendx_hat = (sum(VN_array)' + llr) < 0;%Belief propagation Decision.parity_check = zeros(M, 1);for m = 1 : Mfor k = 1 : 1 : cn_degree(m)parity_check(m) = parity_check(m) + x_hat(H_row_one_absolute_index(m, k));endendif ~sum(mod(parity_check, 2))%early stop, to see whether Hx = 0.iter_this_time = t;break;end
end

注：以上代码并不是最优的，最优算法参见上一篇博文。