LeetCode

受限条件下课到达节点的数目

题目链接：2368. 受限条件下可到达节点的数目 - 力扣（LeetCode）

题目描述

现有一棵由 n 个节点组成的无向树，节点编号从 0 到 n - 1 ，共有 n - 1 条边。

给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。

在不访问受限节点的前提下，返回你可以从节点 0 到达的 最多 节点数目*。*

注意，节点 0 不 会标记为受限节点。

示例 1：

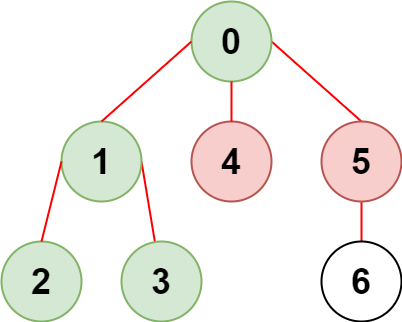
输入：n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
输出：4
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,1,2,3] 可以从节点 0 到达。

示例 2：

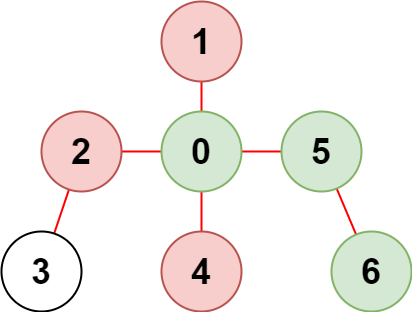
输入：n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
输出：3
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,5,6] 可以从节点 0 到达。

提示：

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges 表示一棵有效的树
• 1 <= restricted.length < n
• 1 <= restricted[i] < n
• restricted 中的所有值 互不相同

思路

灵神题解

2368. 受限条件下可到达节点的数目 - 力扣（LeetCode）

代码

C++

class Solution {vector<vector<int>> g;int dfs(int x,int fa){int cnt = 1;for(int y : g[x]){if(y != fa){cnt += dfs(y,x);}}return cnt;}public:int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {unordered_set<int> r(restricted.begin(),restricted.end());g.resize(n);for(auto &e : edges){int x = e[0], y = e[1];if(!r.contains(x) && !r.contains(y)){g[x].push_back(y); g[y].push_back(x);}}return dfs(0,-1);}
};

Java

class Solution {public int reachableNodes(int n, int[][] edges, int[] restricted) {boolean[] isRestricted = new boolean[n];for(int x : restricted){isRestricted[x] = true;}List<Integer>[] g = new ArrayList[n];Arrays.setAll(g,i -> new ArrayList<>());for(int[] e : edges){int x = e[0],y = e[1];if(!isRestricted[x] && !isRestricted[y]){g[x].add(y);g[y].add(x);}}return dfs(0,-1,g);}private int dfs(int x, int fa, List<Integer>[] g){int cnt = 1;for(int y : g[x]){if(y != fa){cnt += dfs(y,x,g);}}return cnt;}
}