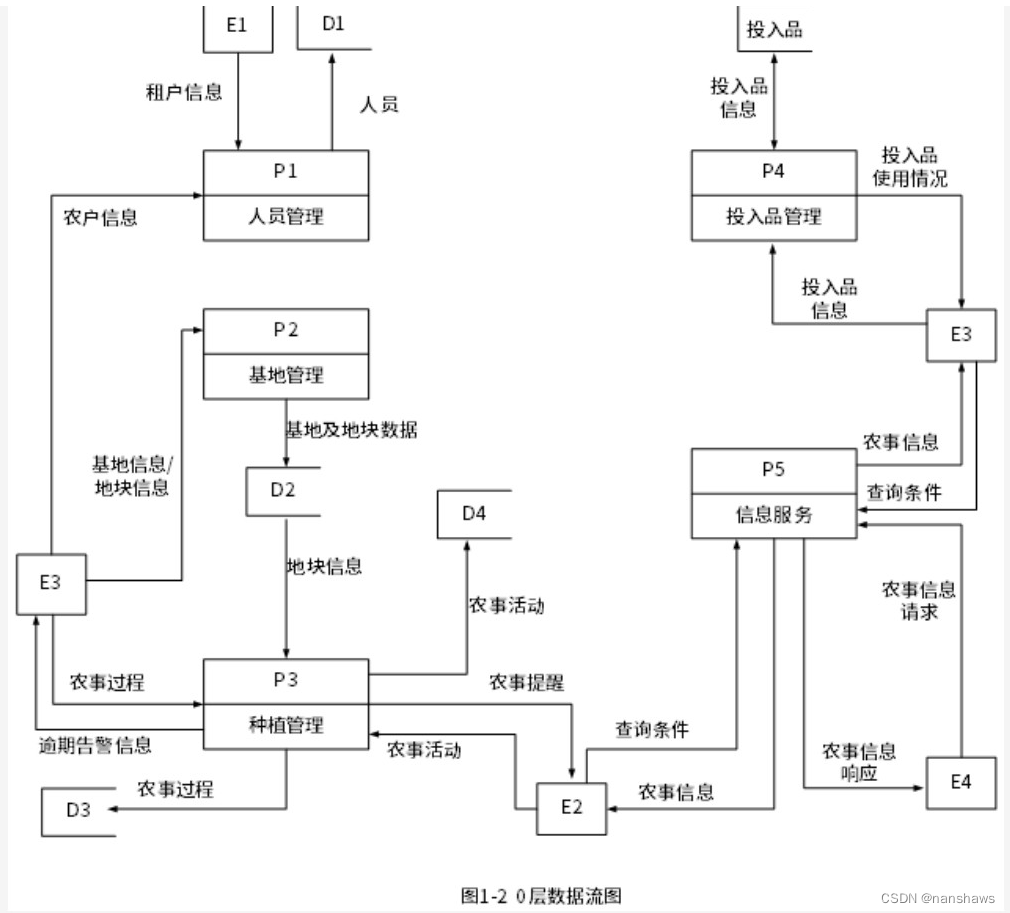
集合

集合（Set）是数学中的一个基本概念，它指的是一组对象的集合，其中的对象称为集合的元素。集合具有以下特性：

无序性：集合中的元素没有固定的顺序，即改变集合中元素的排列顺序不会改变集合本身。

互异性：集合中的元素是互不相同的，即每个元素在集合中只能出现一次。

确定性：集合中的元素是确定的，即每个元素要么属于该集合，要么不属于该集合，没有模糊的中间状态。

在数学中，集合通常使用大括号 {} 来表示，例如 {1, 2, 3} 表示一个包含元素 1、2、3 的集合。如果集合为空，即不包含任何元素，则称为空集，用符号 ∅ 来表示。

集合之间可以进行各种运算，如并集、交集、差集等。并集是指两个集合中所有元素的集合，用符号 ∪ 来表示；交集是指两个集合中共同的元素的集合，用符号 ∩ 来表示；差集是指一个集合中但不在另一个集合中的元素的集合，用符号 - 或 \ 来表示。

创建两个集合：

A = {1, 2, 3, 4}  B = {3, 4, 5, 6}

交集

交集是集合论中的一个基本概念，它指的是两个或多个集合中共同的元素组成的集合。换句话说，如果集合A和集合B的交集是C，那么C中的每一个元素都是A和B的共同元素。

在数学中，交集通常用符号"∩"来表示。例如，如果A和B是两个集合，那么A和B的交集可以表示为A∩B。如果A∩B=C，那么C就是A和B的交集，即C中的元素都是A和B的共同元素。

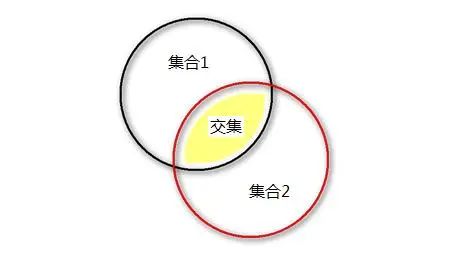
除了数学中的交集，日常生活中也会用到类似的概念。例如，两个朋友圈之间的交集可能指的是共同认识的朋友；两个学科之间的交集可能指的是它们共同的研究领域或知识点。

intersection_set = A.intersection(B)  # 或者使用 A & B  print(intersection_set)  # 输出：{3, 4}

互斥

互斥是集合论中的一个概念，它表示两个集合没有公共的元素，即它们是完全不同的。如果两个集合A和B互斥，那么它们的交集A∩B将是一个空集，即没有任何元素同时属于A和B。

在数学中，互斥通常用符号"∩"和"="来表示。例如，如果A和B是两个互斥的集合，那么A∩B=∅，即它们的交集是一个空集。

互斥与集合的其他关系（如包含、相等）不同。例如，如果集合A包含集合B，那么B中的所有元素都是A中的元素，但A中可能还包含其他元素。而如果集合A和B相等，那么它们包含的元素完全相同。但在互斥的情况下，A和B中的元素完全不同，没有任何交集。

互斥的概念在概率论和统计学中也非常重要。例如，如果两个事件是互斥的，那么它们同时发生的概率是0，因为它们的交集是一个空集。这有助于我们更好地理解和计算复杂事件的概率。

并集

并集是集合论中的一个基本概念，表示两个或多个集合中所有元素的集合。换句话说，如果集合A和集合B的并集是C，那么C中的元素来自A或B或同时来自A和B。

在数学中，并集通常用符号"∪"来表示。例如，如果A和B是两个集合，那么A和B的并集可以表示为A∪B。如果A∪B=C，那么C就是A和B的并集，即C中的元素都是A或B的元素。

与交集不同，并集包含的是所有属于A或属于B的元素，而不仅仅是它们共同拥有的元素。这也意味着，并集中的元素可能只属于A，可能只属于B，也可能同时属于A和B。因此，并集通常比交集包含更多的元素。

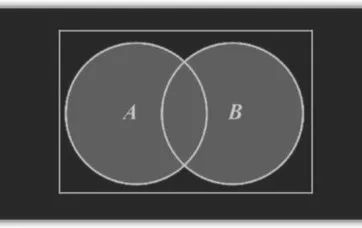
并集运算满足一些基本的性质，例如交换律、结合律和幂等律等。这些性质使得并集运算在数学和其他领域中具有广泛的应用。

除了数学中的并集，日常生活中也会用到类似的概念。例如，两个商店的商品并集可能是它们所有商品的集合；两个国家的语言并集可能是它们所有语言的集合。

union_set = A.union(B)  # 或者使用 A | B  print(union_set)  # 输出：{1, 2, 3, 4, 5, 6}

补集

补集是集合论中的一个重要概念，它指的是一个集合中所有不属于另一个集合的元素组成的集合。具体来说，如果集合A和集合B是全集U的两个子集，那么A在U中关于B的补集是由所有属于U但不属于B且属于A的元素组成的集合。

补集通常用符号"−"或""来表示。例如，如果A和B是全集U的子集，那么A在U中关于B的补集可以表示为A−B或A\B。这个补集中的元素都属于A，但不属于B。

补集有两种主要类型：相对补集和绝对补集。相对补集是指一个集合在另一个集合中的补集，如上所述。而绝对补集则是指一个集合在全集中的补集，即该集合中所有不属于该集合的元素组成的集合。绝对补集也称为该集合的余集。

补集运算满足一些基本的性质，例如德摩根定律等。这些性质使得补集运算在数学、逻辑和计算机科学等领域中有广泛的应用。例如，在逻辑中，补集运算可以用于表示“非”的概念；在计算机科学中，补集运算可以用于实现集合的差集、交集和并集等操作。

差

集合之差，也称为集合的差集，是集合论中的一个基本概念。它指的是属于一个集合但不属于另一个集合的所有元素组成的集合。换句话说，如果集合A和集合B是两个集合，那么A与B的差集是由所有属于A但不属于B的元素组成的集合。

在数学中，集合之差通常用符号"−"或""来表示。例如，如果A和B是两个集合，那么A与B的差集可以表示为A−B或A\B。这个差集中的元素都属于A，但不属于B。

差集运算满足一些基本的性质，例如差集运算是不交换的，即A−B和B−A可能不同；差集运算是结合的，即(A−B)−C等于A−(B∪C)；差集运算也满足分配律，即A−(B∩C)等于(A−B)∪(A−C)。

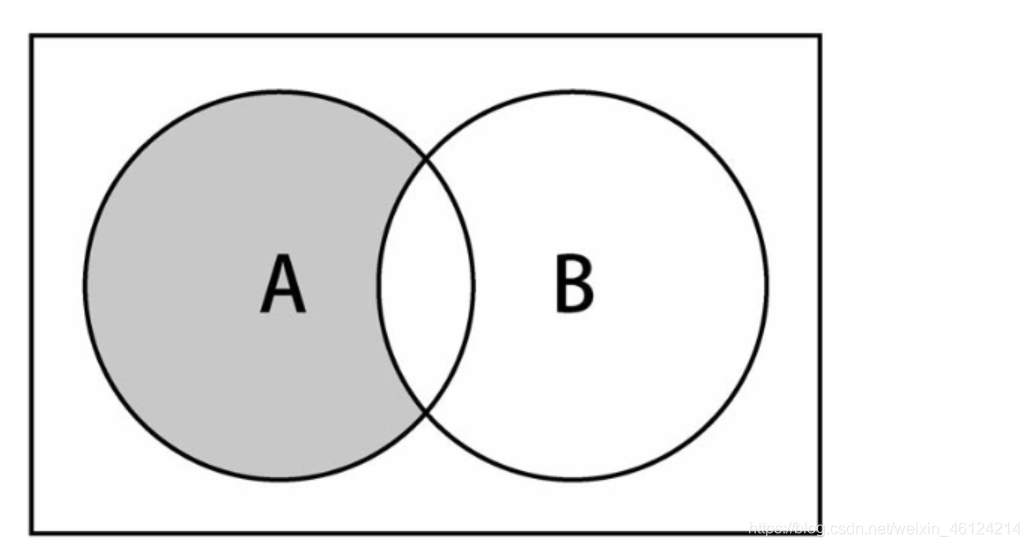
差集运算在实际中有许多应用。例如，在几何中，差集运算可以用来表示不同形状之间的关系；在概率论中，差集运算可以用来计算条件概率；在数据库中，差集运算可以用来进行数据查询；在编程中，差集运算可以用来处理两个集合之间的关系。

difference_set = A.difference(B)  # 或者使用 A - B  print(difference_set)  # 输出：{1, 2}