作业评阅:
概念
1.问题

2.问题(略)

4.问题(略)
(a)问题(略)
10%,忽略 X < 0.05和 X > 0.95的情况。
(b)问题(略)
1%
(c)问题(略)
0.10^(100)∗100=10^(−98)%
(d)
随着p的现象增大,几何上观测值接近指数减少。
(e)
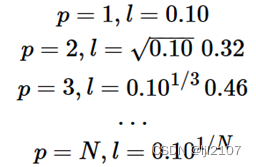
5.问题(略)
(a)问题(略)
如果贝叶斯决策边界是线性的,我们期望 QDA 在训练集上表现得更好,因为它更高的灵活性将产生更接近的匹配。在测试集上,我们预期 LDA 的表现会优于 QDA,因为 QDA 可能会超出贝叶斯决策边界的线性度。
(b)问题(略)
如果贝叶斯决策边界是非线性的,我们期望 QDA 在训练集和测试集上都能表现得更好。
(c)问题(略)
我们期望 QDA 相对于 LDA 的测试预测精度能够随着样本容量n的增加而提高,因为更灵活的方法将产生更好的拟合,更多的样本可以拟合和方差抵消了更大的样本量。
(d)
错误。因为QDA可能会产生过拟合,从而使得测试误差增大。
6.问题(略)

8.问题(略)
逻辑斯蒂回归训练误差为20%,测试误差为30%,平均误差为25%。
1最近邻算法平均错误率18%,但是由于其训练误差为0%,所以其测试误差为36%,大于逻辑斯蒂回归,因此最终选择逻辑斯蒂回归进行新的预测。
9.问题(略)
(a)问题(略)
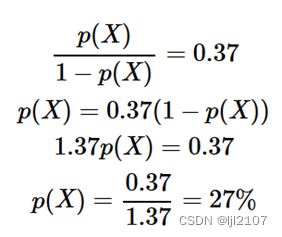
(b)问题(略)
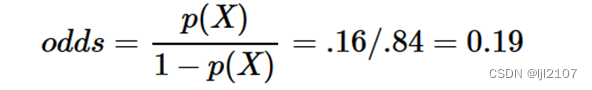
、、、、、、
应用
10.问题(略)
(a)问题(略)
library(ISLR)
summary(Weekly)

Pairs(Weekly)

Cor(Weekly[,-9])
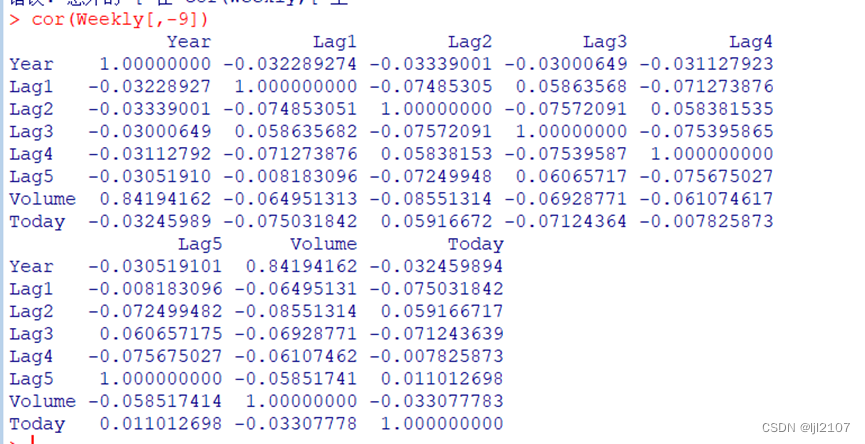
Year和Volume有一定关联,没有发现模式。
(b)问题(略)
attach(Weekly)
glm.fit = glm(Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume, data = Weekly,
family = binomial)
summary(glm.fit)
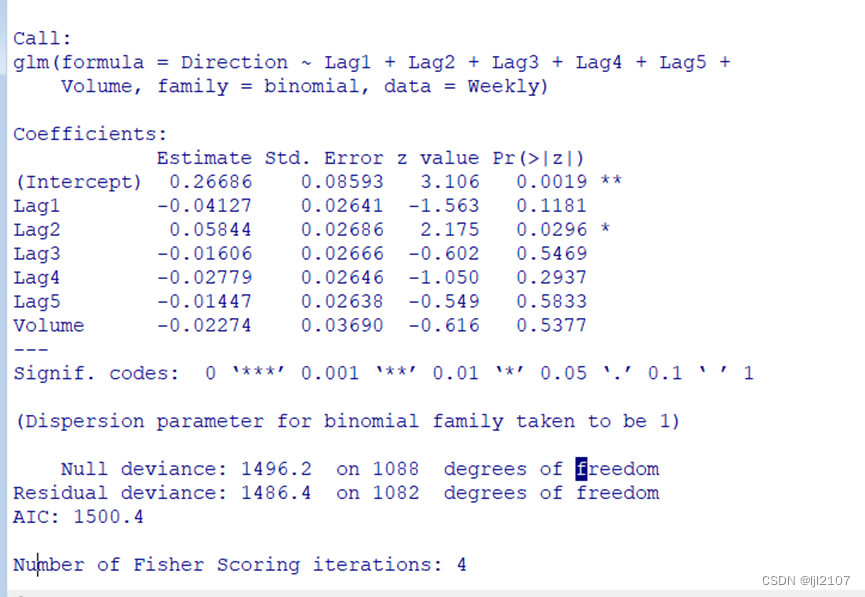
Lag2的p值较小有一定的统计学意义。
(c)问题(略)
glm.probs = predict(glm.fit, type = "response")
glm.pred = rep("Down", length(glm.probs))
glm.pred[glm.probs > 0.5] = "Up"
table(glm.pred, Direction)

总体预测正确率56.1%。但是依然可以看到错误率较高。
(d)
train = (Year < 2009)
Weekly.0910 = Weekly[!train, ]
glm.fit = glm(Direction ~ Lag2, data = Weekly, family = binomial, subset = train)
glm.probs = predict(glm.fit, Weekly.0910, type = "response")
glm.pred = rep("Down", length(glm.probs))
glm.pred[glm.probs > 0.5] = "Up"
Direction.0910 = Direction[!train]
table(glm.pred, Direction.0910)
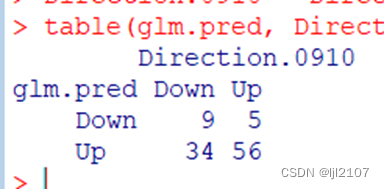
mean(glm.pred == Direction.0910)

(e)
library(MASS)
lda.fit = lda(Direction ~ Lag2, data = Weekly, subset = train)
lda.pred = predict(lda.fit, Weekly.0910)
table(lda.pred$class, Direction.0910)
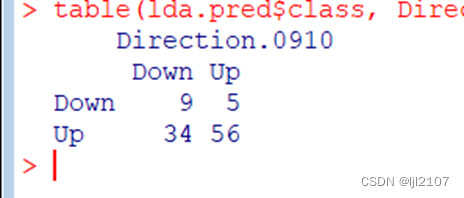
mean(lda.pred$class == Direction.0910)

(f)
qda.fit = qda(Direction ~ Lag2, data = Weekly, subset = train)
qda.class = predict(qda.fit, Weekly.0910)$class
table(qda.class, Direction.0910)
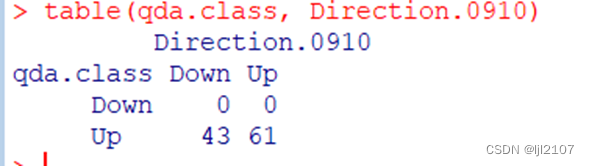
mean(qda.class == Direction.0910)

(g)
library(class)
train.X = as.matrix(Lag2[train])
test.X = as.matrix(Lag2[!train])
train.Direction = Direction[train]
set.seed(1)
knn.pred = knn(train.X, test.X, train.Direction, k = 1)
table(knn.pred, Direction.0910)
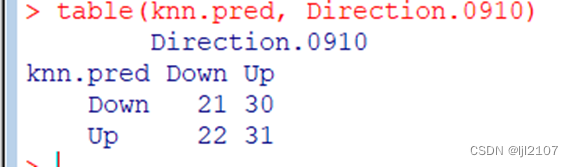
mean(knn.pred == Direction.0910)

(h)
比较而言,逻辑斯蒂回归和LDA方法结果最好。
(i)
逻辑斯蒂回归Lag2:Lag1
glm.fit = glm(Direction ~ Lag2:Lag1, data = Weekly, family = binomial, subset = train)
glm.probs = predict(glm.fit, Weekly.0910, type = "response")
glm.pred = rep("Down", length(glm.probs))
glm.pred[glm.probs > 0.5] = "Up"
Direction.0910 = Direction[!train]
table(glm.pred, Direction.0910)
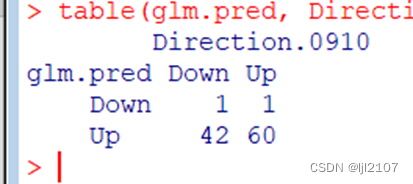
mean(glm.pred == Direction.0910)

Lag1和Lag2相互作用的LDA
lda.fit = lda(Direction ~ Lag2:Lag1, data = Weekly, subset = train)
lda.pred = predict(lda.fit, Weekly.0910)
mean(lda.pred$class == Direction.0910)
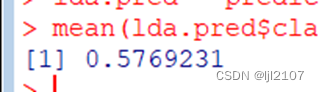
对Lag2绝对值进行平方根后QDA
qda.fit = qda(Direction ~ Lag2 + sqrt(abs(Lag2)), data = Weekly, subset = train)
qda.class = predict(qda.fit, Weekly.0910)$class
table(qda.class, Direction.0910)

mean(qda.class == Direction.0910)
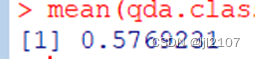
KNN K=10
knn.pred = knn(train.X, test.X, train.Direction, k = 10)
table(knn.pred, Direction.0910)
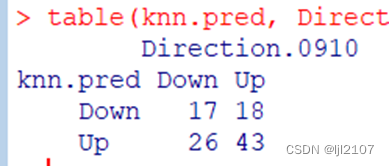
mean(knn.pred == Direction.0910)

KNN K=100
knn.pred = knn(train.X, test.X, train.Direction, k = 100)
table(knn.pred, Direction.0910)

mean(knn.pred == Direction.0910)

11.问题(略)
(a)问题(略)
library(ISLR)
summary(Auto)
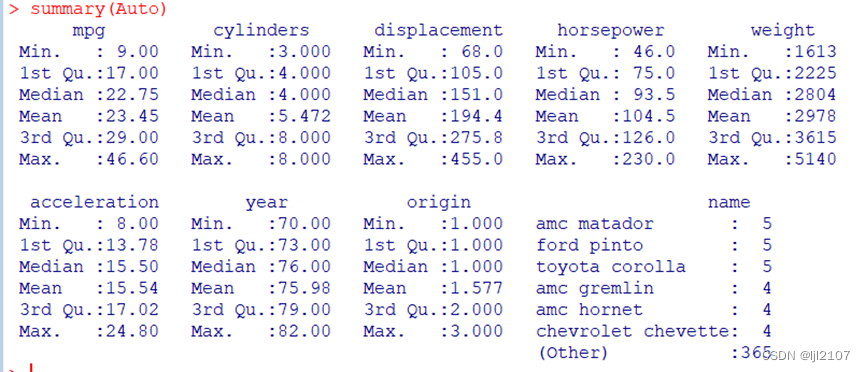
attach(Auto)
mpg01 = rep(0, length(mpg))
mpg01[mpg > median(mpg)] = 1
Auto = data.frame(Auto, mpg01)
(b)问题(略)
cor(Auto[, -9])
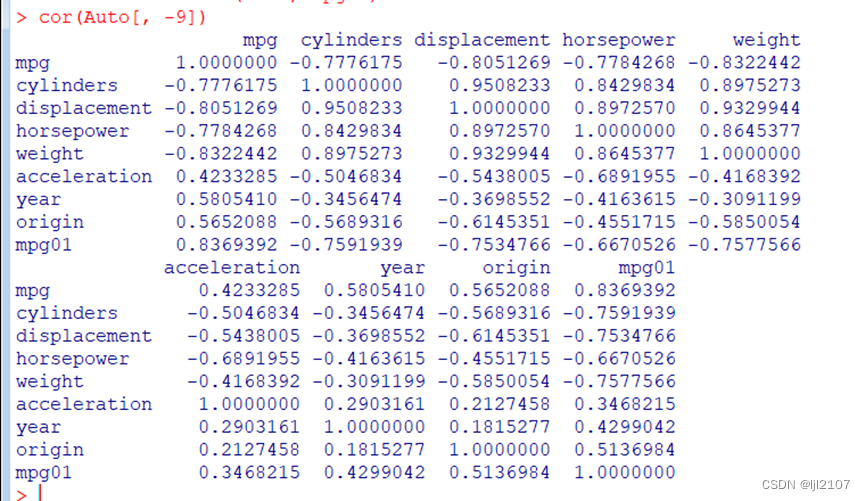
pairs(Auto)

与cylinders, weight, displacement, horsepower有关。
(c)问题(略)
根据年份是否是偶数划分
train = (year%%2 == 0) # 如果年份是偶数
test = !train
Auto.train = Auto[train, ]
Auto.test = Auto[test, ]
mpg01.test = mpg01[test]
(d)
library(MASS)
lda.fit = lda(mpg01 ~ cylinders + weight + displacement + horsepower, data = Auto,
subset = train)
lda.pred = predict(lda.fit, Auto.test)
mean(lda.pred$class != mpg01.test)
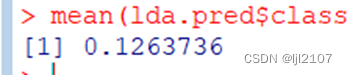
12.6%的错误率
(e)
qda.fit = qda(mpg01 ~ cylinders + weight + displacement + horsepower, data = Auto,
subset = train)
qda.pred = predict(qda.fit, Auto.test)
mean(qda.pred$class != mpg01.test)

13.2%的错误率。
(f)
glm.fit = glm(mpg01 ~ cylinders + weight + displacement + horsepower, data = Auto,
family = binomial, subset = train)
glm.probs = predict(glm.fit, Auto.test, type = "response")
glm.pred = rep(0, length(glm.probs))
glm.pred[glm.probs > 0.5] = 1
mean(glm.pred != mpg01.test)
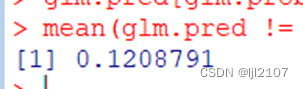
12.1%的错误率。
(g)
library(class)
train.X = cbind(cylinders, weight, displacement, horsepower)[train, ]
test.X = cbind(cylinders, weight, displacement, horsepower)[test, ]
train.mpg01 = mpg01[train]
set.seed(1)
# KNN(k=1)
knn.pred = knn(train.X, test.X, train.mpg01, k = 1)
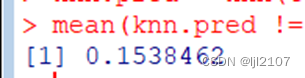
mean(knn.pred != mpg01.test)
KNN(k=10)
knn.pred = knn(train.X, test.X, train.mpg01, k = 10)
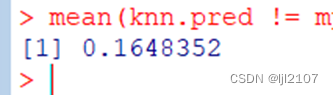
mean(knn.pred != mpg01.test)
KNN(k=100)
knn.pred = knn(train.X, test.X, train.mpg01, k = 100)
mean(knn.pred != mpg01.test)

K=100,14.3%
K=10,16.5%
K=1,15.4%
可以看到K的值为100时,错误率最小。
12.问题(略)
(a)问题(略)
Power = function() {
2^3
}
print(Power())

(b)问题(略)
Power2 = function(x, a) {
x^a
}
Power2(3, 8)

(c)问题(略)
Power2(10, 3)
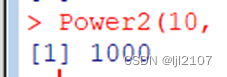
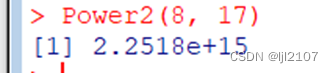
Power2(8, 17)
Power2(131, 3)
(d)
Power3 = function(x, a) {
result = x^a
return(result)
}
(e)
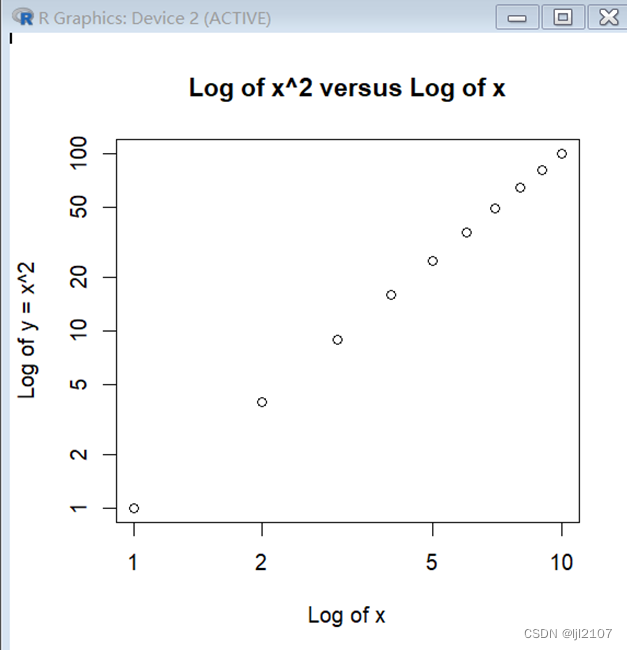
x = 1:10
plot(x, Power3(x, 2), log = "xy", ylab = "Log of y = x^2", xlab = "Log of x",
main = "Log of x^2 versus Log of x")
(f)
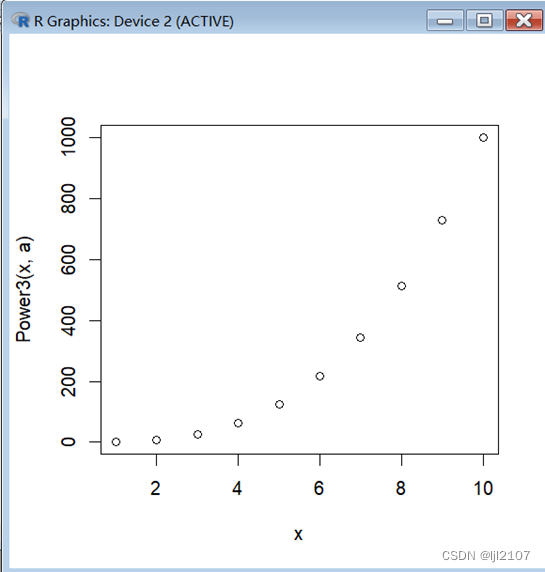
PlotPower = function(x, a) {
plot(x, Power3(x, a))
}
PlotPower(1:10, 3)
后面有需要请私聊吧,不想再粘贴