递归与回溯2

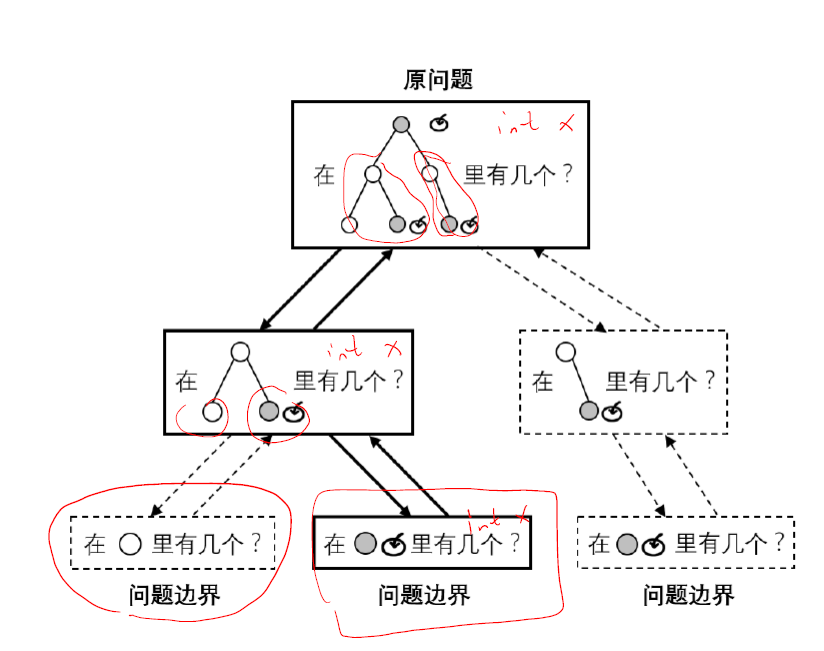
一：递归分治

什么是递归？

  • 函数自己调用自己
  • 通过函数体来进行循环
  • 以自相似的方法重复进行的过程

递归的过程：先自顶向下找到递归出口，在自底向上回到最初的递归位置

在这里插入图片描述

推导路径未知的题目只能用递归不能用循环

比如求多叉树的节点（每个节点的分支都不同）
在这里插入图片描述

推导路径未知的题目只能用递归不能用循环

比如求多叉树的节点（每个节点的分支都不同）

在这里插入图片描述

递归问题需要考虑

  • 确定递归的重叠子问题—数学归纳法
  • 确定递归边界，一定要有递归出口—避免死循环
  • 保护和还原现场—比如当前层的改变了全局参数回溯会影响结果

在这里插入图片描述

一般来说，涉及全局变量和静态变量或者类私有变量，不同层之间可能需要进行数据恢复

二：打印二进制回溯解法

下图是长度为2的二进制个数

  • 从左至右，依次加入0，回溯时放弃0，选择1

先添加元素，后进行递归

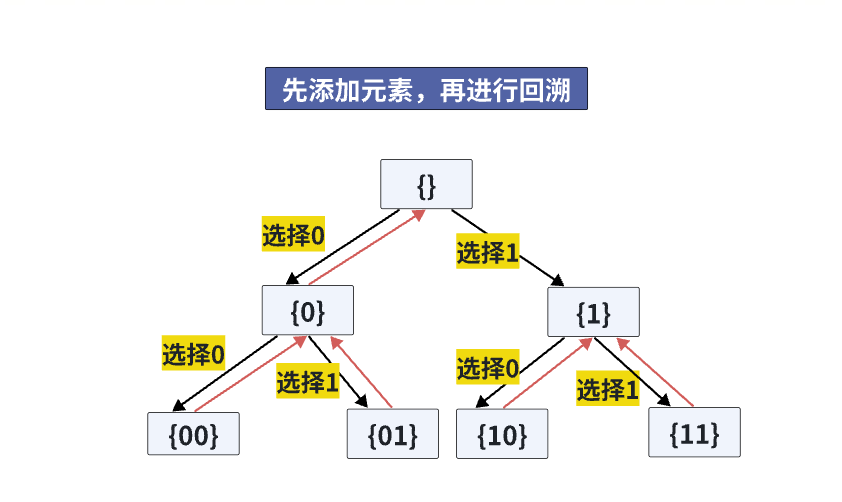
在这里插入图片描述

这种方法一定要传递供选项，就是每次进行的选择

  • 这里二进制的01选择是隐藏的，需要显式给出
vector<vector<int>> res;
void getAllBin(vector<int> nums,vector<int> ans,int n){for (int i = 0; i < nums.size();i++){ans.push_back(nums[i]);//先添加元素if(ans.size()==n){//满足存结果，不要returnres.push_back(ans);}else{//不满足长度递归getAllBin(nums, ans, n);}ans.pop_back();}
}
vector<vector<int>> printAllbin(int n){vector<int> nums = {0, 1};//显式给出01供选项vector<int> ans;getAllBin(nums, ans, n);return res;
}

当然也可以把判断语句放在if外，需要return

void getAllBin(vector<int> nums,vector<int> ans,int n){if(ans.size()==n){//满足存结果res.push_back(ans);return;}for (int i = 0; i < nums.size();i++){ans.push_back(nums[i]);//先添加元素//递归getAllBin(nums, ans, n);ans.pop_back();}
}

一般选择这种，更清晰

先进行回溯，再添加元素

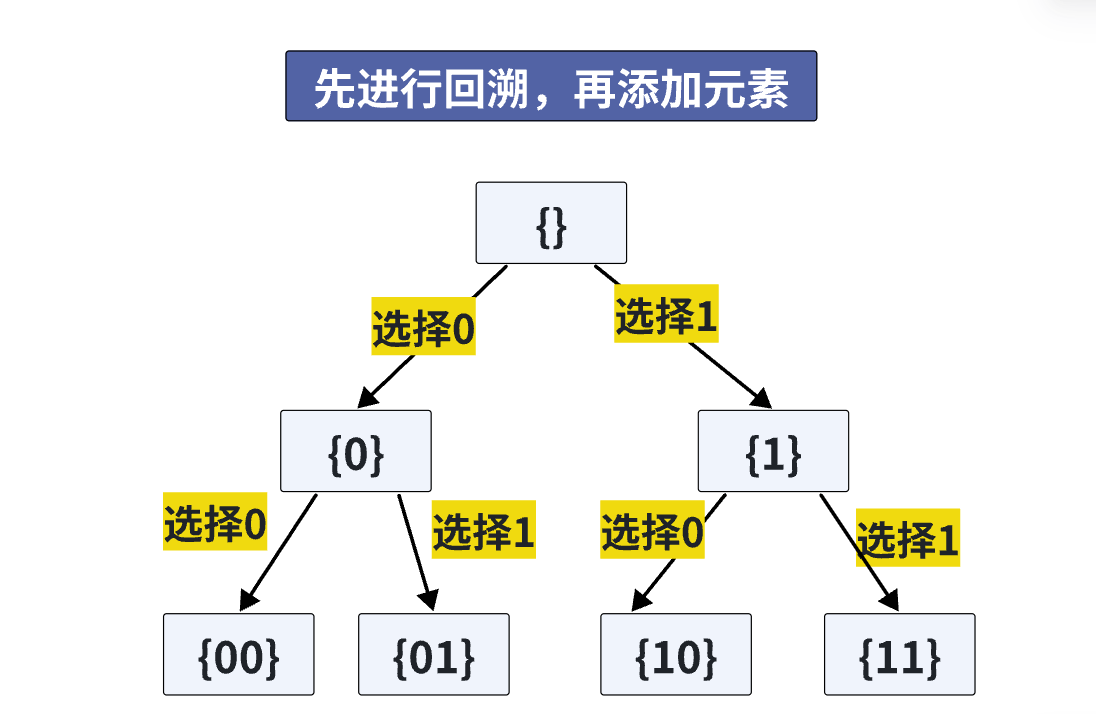
在这里插入图片描述

vector<vector<int>> res;
void getAllBin(vector<int> ans,int n){if(ans.size()==n){res.push_back(ans);return;}//加入0回溯vector<int> tmp1 = ans;tmp1.push_back(0);getAllBin(tmp1, n);//加入1回溯vector<int> tmp2 = ans;tmp2.push_back(1);getAllBin(tmp2, n);
}
vector<vector<int>> printAllbin(int n){vector<int> ans;getAllBin(ans, n);return res;
}

这里是传入新变量，当然也可以用ans，但是需要pop_back(),防止影响结果

void getAllBin(vector<int> ans,int n){if(ans.size()==n){res.push_back(ans);return;}//加入0回溯ans.push_back(0);getAllBin(ans, n);//别忘了pop_back()ans.pop_back();// 加入1回溯ans.push_back(1);getAllBin(ans, n);//pop与否都可以//ans.pop_back();
}

这里ans.size()是隐式递归结束变量，也可以单独用一个参数，但是要注意递归+1

vector<vector<int>> res;
void getAllBin(vector<int> ans,int n,int level){if(level==n){res.push_back(ans);return;}//加入0回溯ans.push_back(0);getAllBin(ans, n, level + 1);//+1ans.pop_back();// 加入1回溯ans.push_back(1);getAllBin(ans, n, level + 1);//+1//pop与否都可以return;
}
vector<vector<int>> printAllbin(int n){vector<int> ans;getAllBin(ans, n,0);//从0开始return res;
}

当然也可以用减法实现，size==0一样可以结束递归

vector<vector<int>> res;
void getAllBin(vector<int> ans,int n){if(n==0){res.push_back(ans);return;}//加入0回溯ans.push_back(0);getAllBin(ans, n-1);//+1ans.pop_back();// 加入1回溯ans.push_back(1);getAllBin(ans, n-1);//+1//pop与否都可以return;
}
vector<vector<int>> printAllbin(int n){vector<int> ans;getAllBin(ans, n);return res;
}

三：用数组初始化一个二叉搜索树

BST数据结构，中序遍历

  • bst数据结构
struct bst{//节点，左子树，右子树int val;bst *left;bst *right;//带有默认参数的构造函数bst(int v = 0,bst* l=NULL,bst* r=NULL):val(v),left(l),right(r){}
};
  • 中序遍历
void midTraverse(const bst* root){if(root==NULL)return;midTraverse(root->left);cout << root->val << " ";midTraverse(root->right);
}
  • 程序测试
int main(){bst *aa = new bst(100);bst *bb = new bst(500);bst *cc = new bst(200, aa, NULL);bst *dd = new bst(400, NULL, bb);bst *ee = new bst(300,cc,dd);midTraverse(ee);return 0;
}

运行结果：

100 200 300 400 500

迭代形式创建

先找后插
bst* createBST_loop(int a[],int n){//首先根节点设为第一个元素值bst *root = new bst(a[0]);//插入余下值bst *parent = NULL;for (int i = 1; i < n;i++){//定义指向root节点，防止断链bst *cur = root;//必须从root开始// 先找到插入值的父节点，再进行插值while (cur){if (a[i] < cur->val){parent = cur;cur = cur->left;}else if (a[i] > cur->val){parent = cur;cur = cur->right;}else{ // a[i]==root->valreturn root;}}//判断当前值和父节点大小来将新节点插入到左右子树if(parent){//防止NULL->__if(a[i]<parent->val){parent->left = new bst(a[i]);}else{parent->right = new bst(a[i]);}}}//forreturn root;
}
  • 需要一个指针指向root，这样每次才能不断链
  • 这里是找到插入节点的父节点，单独标记

当然也可以把根节点作为参数，函数没有返回值

  1. 但是必须传入指针的引用

  2. 传引用，初始化必须有指向，比如NULL

void create_BST_loop(bst*& root,int a[],int n){root = new bst(a[0]);bst *parent = NULL;for (int i = 1; i < n;i++){bst *cur = root;while(cur){if(a[i]<cur->val){parent = cur;cur = cur->left;}else if(a[i]>cur->val){parent = cur;cur = cur->right;}else{return;}}//待插节点bst *tmp = new bst(a[i]);if(parent){if(a[i]<parent->val){parent->left = tmp;}else{parent->right = tmp;}}}//for
}

bst *newnode=NULL;

create_BST_loop(newnode, a, n);

midTraverse(newnode);

边找边插
bst* create_BST_loop(int a[],int n){bst* root = new bst(a[0]);for (int i = 1; i < n;i++){bst *cur = root;while(cur){if(a[i]<cur->val){if(cur->left){cur = cur->left;}else{cur->left = new bst(a[i]);break;//插入后跳出}}else if(a[i]>cur->val){if(cur->right){cur = cur->right;}else{cur->right = new bst(a[i]);break;}}else{return root;}}}//forreturn root;
}

  • 这里不需要父节点了，只要往左右子树遍历时判断一下存在性

    不存在说明该左子树就是要插值

  • 千万别忘了插入后的break

递归形式创建

由于每次插入需要找到插入位置，所以用递归找到插入位置，然后循环多次插入

void getRecursion(bst*& root,int x){if(root==NULL){root = new bst(x);return;}if(x<root->val){getRecursion(root->left, x);}else if(x>root->val){getRecursion(root->right, x);}else{//==return;} 
}
bst* create_BSTrecursion(int a[],int n){bst *root = new bst(a[0]);for (int i = 0; i < n;i++){int x = a[i];getRecursion(root, x);}return root;
}
  • 父节点形式递归,返回类型bst*
bst* getRecursion(bst* root,int x){if(root==NULL){root = new bst(x);return root;}if(x<root->val){//自己建立链条root->left = getRecursion(root->left, x);}else if(x>root->val){root->right = getRecursion(root->right, x);}return root;
}
bst* create_BSTrecursion(int a[],int n){bst *root = new bst(a[0]);// bst* tmp;for (int i = 0; i < n;i++){int x = a[i];getRecursion(root, x);//tmp=getRecursion(root, x);}return root;//return tmp
} 

bst* create_BSTrecursion(int a[],int n){bst *root = new bst(a[0]);bst* tmp;for (int i = 0; i < n;i++){int x = a[i];tmp=getRecursion(root, x);}return tmp
}

可以定义新变量接受返回值，因为root在函数内部，可以不写root=getRecyrsion();

  • 如果想变成void,就需要把父节点作为参数
void getRecursion(bst* root,bst* parent,int x){if(root==NULL){/*建立parent与root联系*/if(x<parent->val){parent->left = new bst(x);}else{parent->right = new bst(x);}return;//递归结束}//传递父节点if(x<root->val){getRecursion(root->left,root, x);}else if(x>root->val){getRecursion(root->right,root,x);}return;
}
bst* create_BSTrecursion(int a[],int n){bst *root = new bst(a[0]);for (int i = 0; i < n;i++){int x = a[i];getRecursion(root,NULL, x);}return root;
}

主函数形式

bst不可以有重复值，所以生成随机数时候需要去重

int n = 10;int *a = new int[10];for (int i = 0; i < 10;i++){//生成[a,b)的随机数---(rand()%(b-a))+aa[i] = (rand() % 90)+10;//bst不能有重复值，相等去除for (int j = 0; j < i;j++){if(a[j]==a[i]){i-=1;//重新生成a[i]break;}}}// bst *root = create_BSTrecursion(a, n);

四：换一种思路求全排列

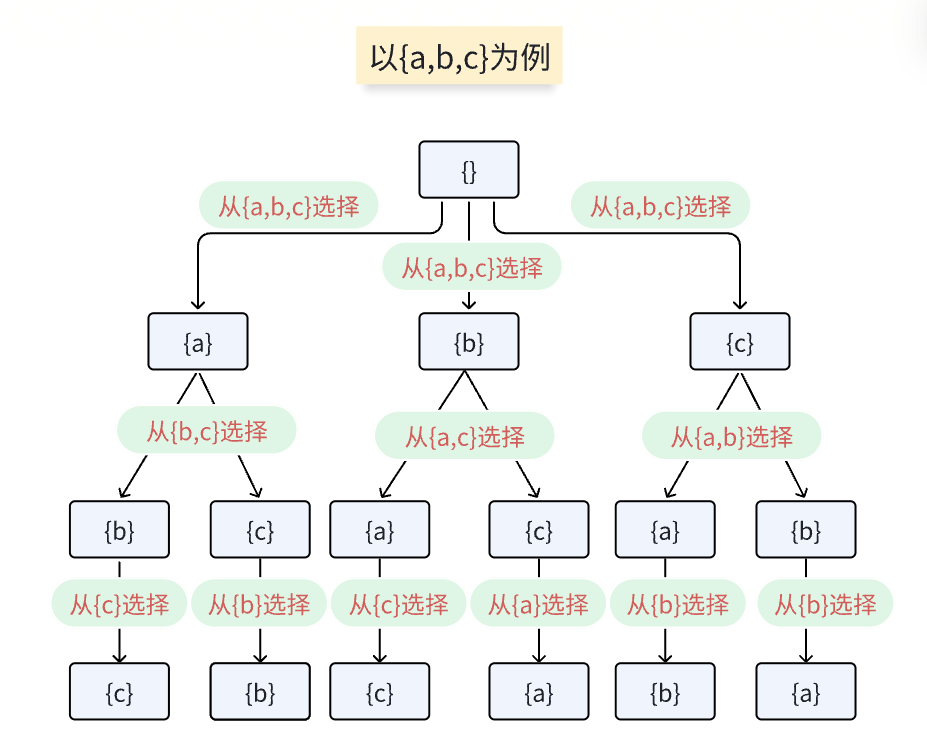
在这里插入图片描述

也就是变动原数组，选择一个就把自己的选择去掉，然后递归，回溯的时候补上元素

​ 把数组恢复需要用到insert()函数，需要传递插入位置和插入值:

​ 所以在删除的时候提前记录删除元素值和删除的iter位置

vector<vector<int>> res;
void getLine(vector<int> nums ,vector<int> ans,int n){if(n==0){res.push_back(ans);return;}for (int i = 0; i < nums.size();i++){//记录删除元素xint x = nums[i];ans.push_back(nums[i]);//记录删除元素位置的下一个迭代器itauto it=nums.erase(nums.begin()+i);getLine(nums, ans, n - 1);//别忘了回溯撤销ans的选择ans.pop_back();//恢复原数组，在it前加入xnums.insert(it,x);}
}
vector<vector<int>> fullLine(vector<int> nums){vector<int> tmp;getLine(nums, tmp,nums.size());return res;
}

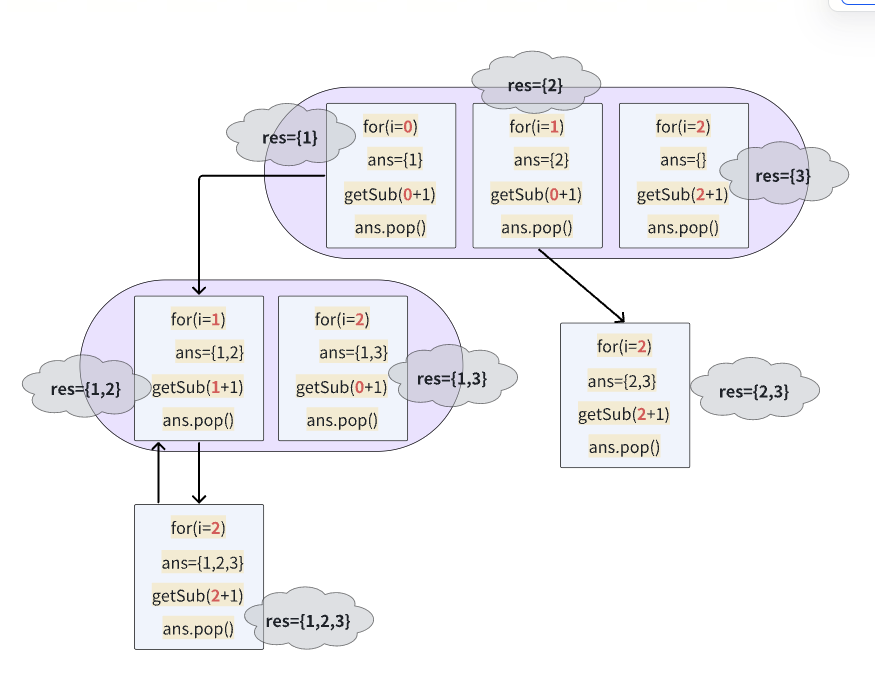
五：求{1，2，3}子集图示

先选元素，再回溯

在这里插入图片描述

由于子集中元素可选可不选，每次循环的开始值是上一次的值+1

class Solution {
public:vector<vector<int>> subsets(vector<int>& nums) {vector<int> mm;findSub(nums, mm, 0);res.push_back({});return res;}private:vector<vector<int>> res;void findSub(vector<int> nums, vector<int> ans, int index) {for (int i = index; i < nums.size(); i++) {ans.push_back(nums[i]);// res.push_back(ans);findSub(nums, ans, i + 1); // 当前i的下一个res.push_back(ans);        // 在递归前记录也行ans.pop_back();}}
};

运行结果：

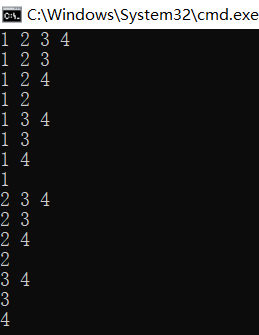
在这里插入图片描述

在这里插入图片描述

六：组合问题

77. 组合
C n k : 从 n 个元素中选 k 个 C_n^k:\text{从}n\text{个元素中选}k\text{个} Cnk​:从n个元素中选k个

其实思路类似子集：

比如{1，2，3}中{1，3}和{3，1}是重复的，所以元素只能以该元素为起点，向后递归，不能往前选

但是组合规定了个数，只要在结果处存储正确的符合条件的结果即可，在所有路径提前剪去不符合要求的

注意：从i开始的，必须要求[i,...,n]的个数n-i+1加上ans当前的数量大于k

即：n-i+1+ans.size()>k----数量小于k一点不符合题意，提前剪枝

class Solution {
public:vector<vector<int>> combine(int n, int k) {this->n=n;this->k=k;vector<int> mm;findCombine(mm,0);return res;}
private:int n;int k;vector<vector<int>> res;void findCombine(vector<int> ans,int index){if(ans.size()==k){res.push_back(ans);return;//递归结束}//[i,...,n]个数：n-i+1+ans.size()<kfor(int i=index;i<(n-k+1)+ans.size();i++){ans.push_back(i+1);findCombine(ans,i+1);ans.pop_back();}}
};

也可以按照选不选元素去回溯，但是要提前结束

  • 当前ans的大小超过k了
  • 当前ans的大小把后面全选了也不足k
class Solution {
public:vector<vector<int>> combine(int n, int k) {this->n = n;this->k = k;vector<int> mm;findCombine(mm, 1);return res;}private:int n;int k;vector<vector<int>> res;void findCombine(vector<int> ans, int index) {// ans.size()+(n-index+1)<kif (ans.size() > k || ans.size() + (n - index + 1) < k) {return; // 提前回溯}if (ans.size() == k) {res.push_back(ans);return;}// 选该元素ans.push_back(index);findCombine(ans, index + 1);// 不选该元素ans.pop_back();findCombine(ans, index + 1);}
};

      // 不选该元素findCombine(ans, index + 1);// 选该元素ans.push_back(index);findCombine(ans, index + 1);

从不选到选，不需要pop_back(),加上也正确

三种基本类型回溯

分为排列，子集，组合，后一种分别是前一种的子集

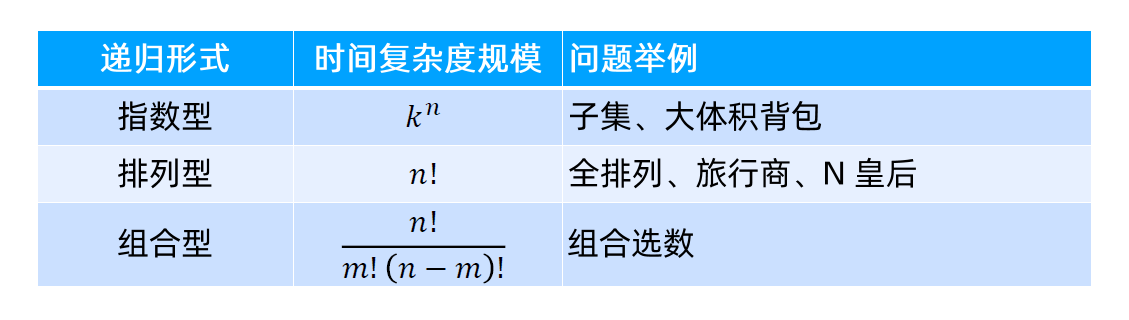
在这里插入图片描述

类似问题只需在该基础上进行剪枝

七：递归与分治

104. 二叉树的最大深度

自底向上求法

分治求法：

  • 求出左子树的最大深度
  • 求出右子树的最大深度
  • 然后最大深度=max(左子树，右子树)+1（根节点）
int maxDepth(TreeNode* root) {if(root==NULL) return 0;int l=maxDepth(root->left);int r=maxDepth(root->right);return max(l,r)+1;}

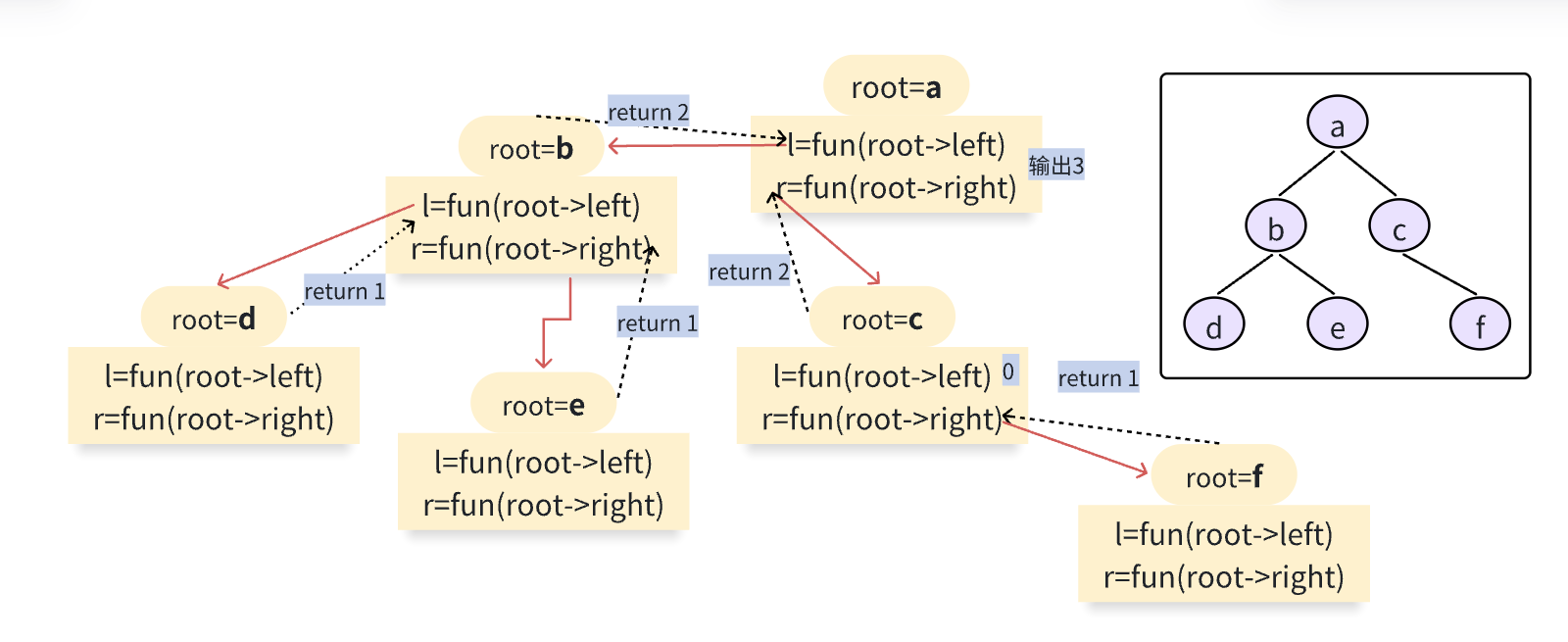
在这里插入图片描述

联系在一起的关键是：函数体内求左子树和求右子树的对应一个root

这是典型的自底向上，也就是相当于从下面向前面追溯得到结果

自顶向下求法

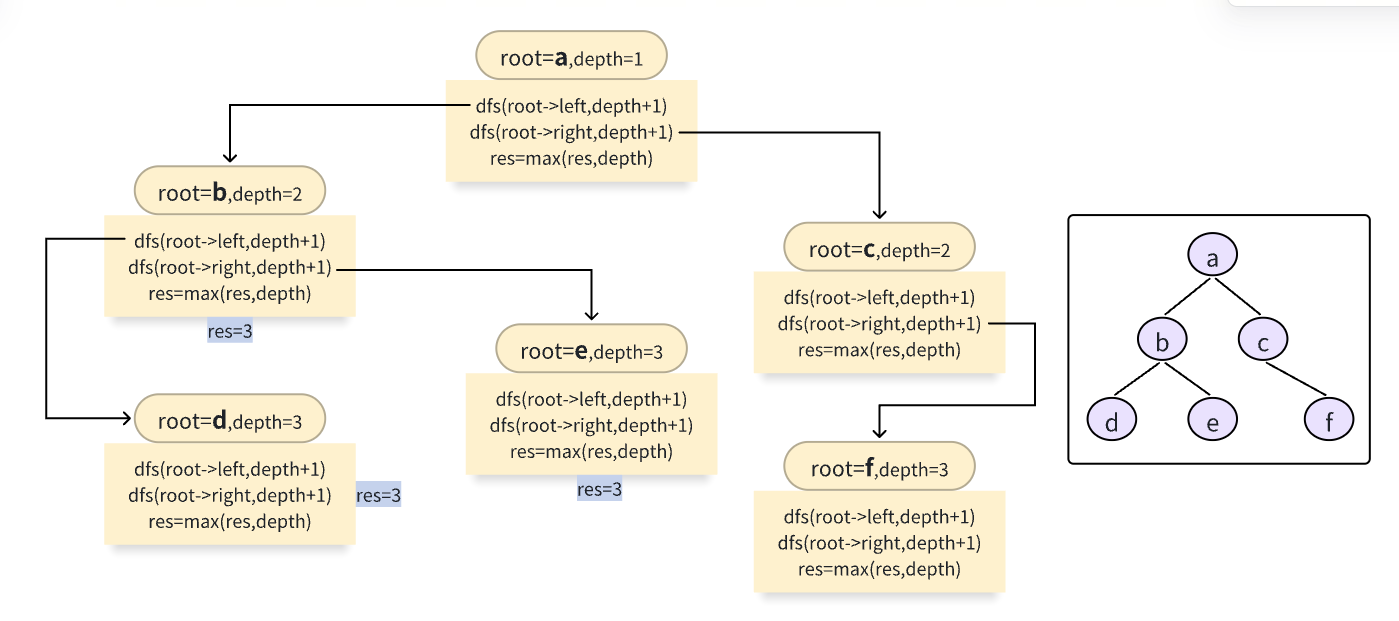
在这里插入图片描述

class Solution {
public:int maxDepth(TreeNode* root) {res = 0;dfs(root, 1);//根节点为1return res;}private:int res;void dfs(TreeNode* root, int depth) {if (root == NULL)return;dfs(root->left, depth + 1);dfs(root->right, depth + 1);res = max(res, depth); // 更新结果}
};

每次递归依次就更新依次结果

递归前或递归后递归不影响

res = max(res, depth); // 更新结果
dfs(root->left, depth + 1);
dfs(root->right, depth + 1);

当然也可以把depth设为全局变量，但是要清理现场

class Solution {
public:int maxDepth(TreeNode* root) {res = 0;depth=0;dfs(root);return res;}private:int res;int depth;void dfs(TreeNode* root) {if (root == NULL)return;depth++;//当前层+1res = max(res, depth); // 更新结果dfs(root->left);//depth--;//depth++;dfs(root->right);depth--;//回到上一层，depth-1}
};

bfs—广度优先遍历

队列存储二元组，每次都记录层次大小

  using pr=pair<TreeNode*,int>;int maxDepth(TreeNode* root) {int res=0;/*广度优先遍历*/queue<pr> que;int level=1;//记录层次if(root==NULL) return 0;que.push(make_pair(root,level));while(!que.empty()){TreeNode* tmp=que.front().first;int level=que.front().second;que.pop();res=max(res,level);//更新resif(tmp->left) que.push(make_pair(tmp->left,level+1));if(tmp->right) que.push(make_pair(tmp->right,level+1));}return res;}

当然也可以利用队列每次存的都是当前层的所有元素

int maxDepth(TreeNode* root) {int res = 0;/*广度优先遍历*/queue<TreeNode*> que;int level = 1; // 记录层次if (root == NULL)return 0;que.push(root);while (!que.empty()) {int sz = que.size(); // 当前队列元素，当前层个数while (sz > 0) {//当前层所有元素出队TreeNode* tmp = que.front();que.pop();if (tmp->left)que.push(tmp->left);if (tmp->right)que.push(tmp->right);sz--;}res+=1;//层次+1}return res}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/504659.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

计算机服务器中了mallox勒索病毒怎么解密，mallox勒索病毒解密流程

计算机服务器中了mallox勒索病毒怎么解密，mallox勒索病毒解密流程

科技技术的第一生产力&#xff0c;网络技术的不断发展与应用&#xff0c;让企业逐步走向数字化时代&#xff0c;通过网络的力量可以为企业更好地开展各项业务工作&#xff0c;网络数据安全问题也由此成为众多企业关心的主要话题。近日&#xff0c;云天数据恢复中心接到某化工集…
阅读更多...
扩展学习|大数据分析的现状和分类

扩展学习|大数据分析的现状和分类

文献来源&#xff1a;[1] Mohamed A , Najafabadi M K , Wah Y B ,et al.The state of the art and taxonomy of big data analytics: view from new big data framework[J].Artificial Intelligence Review: An International Science and Engineering Journal, 2020(2):53. 下…
阅读更多...
【LeetCode:230. 二叉搜索树中第K小的元素 + 二叉树 + 递归】

【LeetCode:230. 二叉搜索树中第K小的元素 + 二叉树 + 递归】

&#x1f680; 算法题 &#x1f680; &#x1f332; 算法刷题专栏 | 面试必备算法 | 面试高频算法 &#x1f340; &#x1f332; 越难的东西,越要努力坚持&#xff0c;因为它具有很高的价值&#xff0c;算法就是这样✨ &#x1f332; 作者简介&#xff1a;硕风和炜&#xff0c;…
阅读更多...
打基础！张宇《30讲》vs 武忠祥《基础篇》

打基础！张宇《30讲》vs 武忠祥《基础篇》

张宇老师和武忠祥老师的课程都很推荐&#xff0c;两个老师也都很有实力 我在考研的时候跟的是张宇老师&#xff0c;然后强化阶段跟的是武忠祥老师&#xff0c;我真实的听过两个老师的课程&#xff0c;所以我觉得我有一些发言权。因此对大家在考研数学备考选择老师方面&#xf…
阅读更多...
在原有pytorch环境下安装DGL库和其对应的CUDA【自用】

在原有pytorch环境下安装DGL库和其对应的CUDA【自用】

前段时间看到一篇AAAI2024的论文Patch-wise Graph Contrastive Learning for Image Translation&#xff0c;它采用GNN的思想来进行image-to-image translation的任务&#xff0c;非常的新颖&#xff0c;但我进行复现的时候&#xff0c;发现直接下载它里面需要的DGL库是无法运行…
阅读更多...
云时代【6】—— 镜像 与 容器

云时代【6】—— 镜像 与 容器

云时代【6】—— 镜像 与 容器 四、Docker&#xff08;三&#xff09;镜像 与 容器1. 镜像&#xff08;1&#xff09;定义&#xff08;2&#xff09;相关指令&#xff08;3&#xff09;实战演习镜像容器基本操作离线迁移镜像镜像的压缩与共享 2. 容器&#xff08;1&#xff09;…
阅读更多...
程序员的金三银四求职宝典！

程序员的金三银四求职宝典！

目录 ​编辑 程序员的金三银四求职宝典 一、为什么金三银四是程序员求职的黄金时期&#xff1f; 二、如何准备金三银四求职&#xff1f; 1. 完善简历 2. 增强技术能力 3. 提前考虑目标公司 4. 提前准备面试 三、程序员求职的常见面试题 1. 数据结构和算法 2. 数据库 …
阅读更多...
深入剖析k8s-Pod篇

深入剖析k8s-Pod篇

为什么需要Pod&#xff1f; 进程是以进程组的方式组织在一起。受限制容器的“单进程模型”&#xff0c; 成组调用没有被妥善处理&#xff08;资源调用有限&#xff09;&#xff0c;使用资源囤积则导致复杂度上升。 在k8s项目中&#xff0c;Pod的实现需要使用一个中间容器——…
阅读更多...
GO—函数

GO—函数

Go 语言支持普通函数、匿名函数和闭包&#xff0c;从设计上对函数进行了优化和改进&#xff0c;让函数使用起来更加方便。 Go 语言的函数属于“一等公民”&#xff08;first-class&#xff09;&#xff0c;也就是说&#xff1a; 函数本身可以作为值进行传递。支持匿名函数和闭…
阅读更多...
css【详解】—— 圣杯布局 vs 双飞翼布局 （含手写清除浮动 clearfix）

css【详解】—— 圣杯布局 vs 双飞翼布局 （含手写清除浮动 clearfix）

两者功能效果相同&#xff0c;实现方式不同 效果预览 两侧宽度固定&#xff0c;中间宽度自适应&#xff08;三栏布局&#xff09;中间部分优先渲染允许三列中的任意一列成为最高列 圣杯布局 通过左右栏填充容器的左右 padding 实现&#xff0c;更多细节详见注释。 <!DOCTYP…
阅读更多...
零拷贝技术深入分析

零拷贝技术深入分析

一、零拷贝 在前面的文章“深浅拷贝、COW及零拷贝”中对零拷贝进行过分析&#xff0c;但没有举例子&#xff0c;也没有深入进行展开分析。本文将结合实际的例程对零拷贝进行更深入的分析和说明。 在传统的IO操作中&#xff0c;以文件通过网络传输为例 &#xff0c;一般会经历以…
阅读更多...
挑战英伟达，需要另辟蹊径

挑战英伟达，需要另辟蹊径

Groq是近期AI芯片界的一个明星。原因是其号称比英伟达的GPU更快。3月2日&#xff0c;据报道&#xff0c;Groq收购了一家人工智能解决方案公司Definitive Intelligence。这是 Groq 在 2022 年收购高性能计算和人工智能基础设施解决方案公司 Maxeler Technologies 后的第二次收购…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023