目录
1 什么是自注意力机制
2 自注意力的计算过程
1 什么是自注意力机制
自注意力机制(Self-Attention)顾名思义就是关注单个序列内部元素之间的相关性,不仅可以用于 seq2seq 的机器翻译模型,还能用于情感分析、内容提取等场景。因此分析网络如何表达出“单个序列”与“内部元素”之间的相关性这一问题可以回答开头所述的大部分疑问。
2 自注意力的计算过程
如图1所示,假设网络某一个自注意力层的输入向量序列为 ,
维度均为
,该层的输出向量序列为
,
的维度同样都为
首先将 分别乘以同一个矩阵
、
、
得到 key 向量
、query 向量
以及 value 向量
,且维度均为
。
然后以 输出到
的过程为例。把
依次与所有的key做点积后得到初步的注意力值
,图1所示。

图1 自注意力计算过程1
然后将 经过 softmax 函数归一化得到最终的注意力权重
,这个
可以看作我们给输入向量序列中的每个位置的向量打分,而这个分数决定了当我们在一个特定的位置处理一个向量时,在输入的句子的其他部分应该给予多少关注。
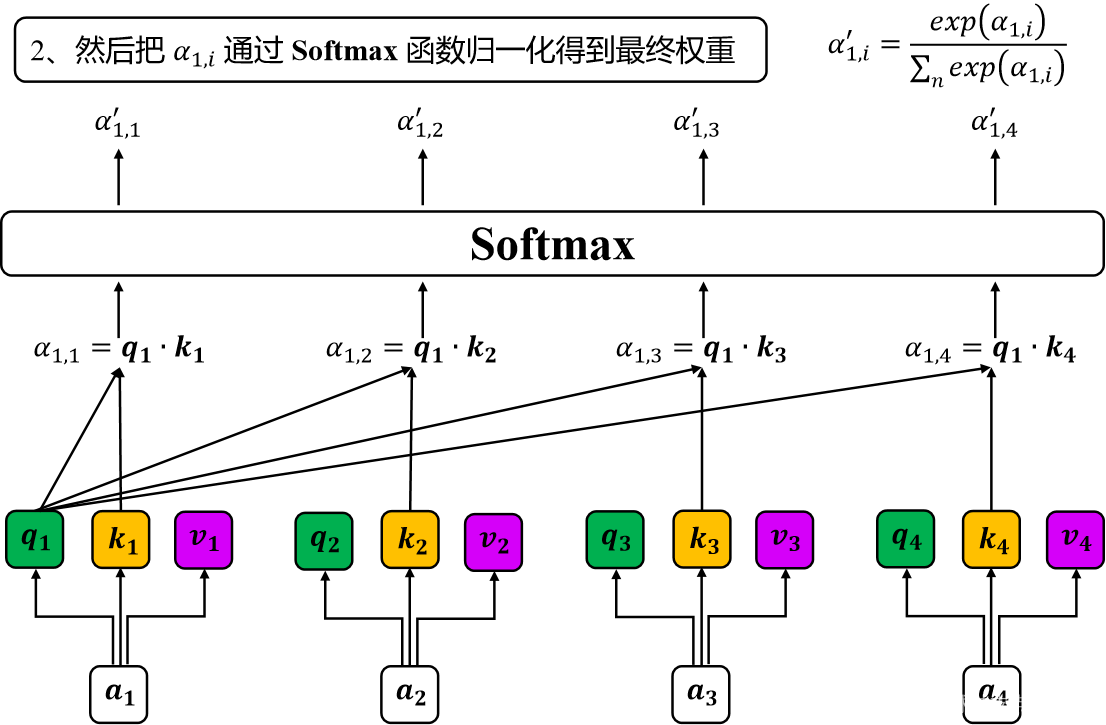
图2 注意力权重计算
将权重 与
加权相乘之后再相加得到
对应的自注意力输出向量
,如图3所示。
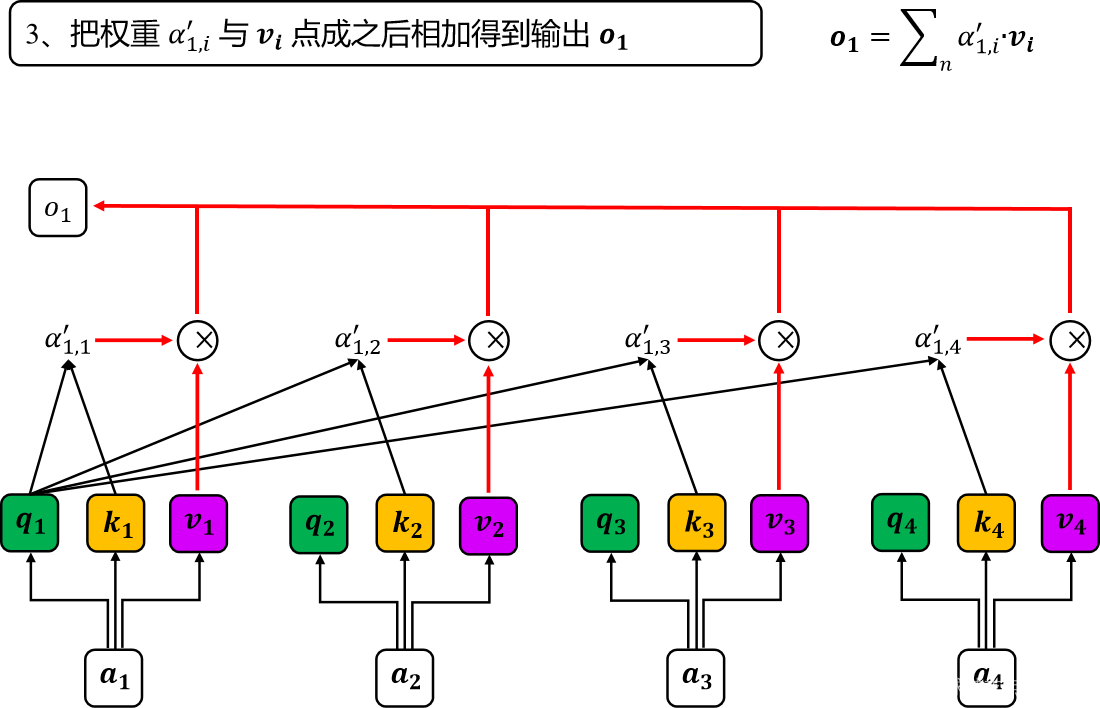
图3 自注意力计算3
其他的计算方法与此相同,最终的计算结果如图4所示。其中 与相应的
的维度相同,都是
整个注意力机制中只有
、
以及
三个矩阵是可学习的参数。

图4 自注意力计算4
进一步地,既然每个输入向量 都是乘以相同的矩阵,那么可以将所有输入向量
整合为一个矩阵
,然后把三种输出向量
、
以及
也整合成矩阵的形式分别为
、
、
,比如
可以写为下式所示的形式:
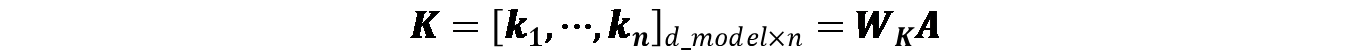
此时的输出矩阵就可以写成下式的结果:
![]()
这里的矩 就是注意力矩阵,代表着当处理当前位置向量时,其他位置的向量对当前位置向量的影响程度。
Transformer中的输出矩阵还乘以了一个缩放系数 ,
是
的维度。所以最终的输出是下式所示的形式:
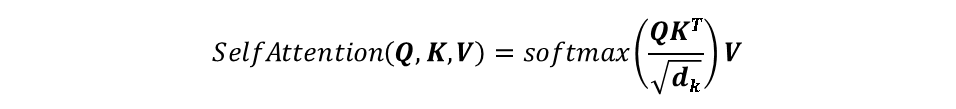
在这里使用矩阵运算的目的是可以提升计算效率。