信号系统之复数-编程知识

1 复数系统

为了说明复杂的数字，考虑一个孩子向空中扔球。假设球是直接向上扔的，初始值速度为每秒9.8米。一秒钟后，球已经达到了4.9米的高度，并且加速度为重力（每秒9.8米2）已将其速度降至零。球然后向地面加速，两秒钟后被孩子抓住在它被抛出之后。根据基本的物理方程，球的高度任何时刻由以下公式给出：

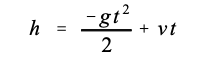
其中 h 是离地高度（以米为单位），g 是重力加速度（9.8 米每秒），v 是初速度（9.8 米每秒），t 是时间（以秒为单位）。

现在，假设想知道球何时经过某个高度。代入已知值并求解 t：

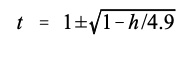
例如，球两次处于3米的高度：t=0.38（向上）和 t=1.62秒（向下）。

只要提出合理的问题，这些方程就会给出合理的答案。但是，当提出不合理的问题时会发生什么呢？例如：球什么时候达到10米的高度？这个问题在现实中没有答案，因为球从来没有达到这个高度。然而，将h=10的值代入上述方程会给出两个答案：
$t=1+\sqrt{-1.041}$ 和 $t=1-\sqrt{-1.041}$ 。这两个答案都包含负数的平方根，这在我们所知的世界上是不存在的。多项式方程的这种不同寻常的性质最早由意大利数学家Girolamo Cardano（1501-1576）使用。两个世纪后，伟大的德国数学家卡尔·弗里德里希·高斯（1777-1855）创造了复数一词，并为现代理解该领域铺平了道路。

每个复数都是两个分量的总和：实部和虚部。实部是一个实数，虚部是虚数，即负数的平方根。为了保持标准化，虚部通常被简化为一个普通数乘以负一的平方根。例如，复数： $t=1+\sqrt{-1.041}$ , 首先简化为： $t=1+\sqrt{1.041}\sqrt{-1}$ ，然后简化为 $t=1+1.02\sqrt{-1}$ 。对于 $\sqrt{-1}$ 数学家长期以来用 i 来表示。相比之下，电气工程师使用符号 j，因为使用了 i 来表示电流。

正如实数被描述为沿着数轴具有位置一样，复数由称为复平面(complex plane)的二维显示中的位置来表示。如图30-1所示，水平轴复平面是复数的实部，而纵轴是虚部。由于实数是虚部为零的复数，因此实数轴与复平面的 x 轴相同。

在数学方程中，复数由单个变量表示，即使它由两部分组成。例如，图30-1中的三个复数变量可以写成：

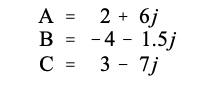
其中 A、B 和 C 是复变量。这说明了使用复数的一个很大的优点和一个很大的缺点：

优点是用一个符号表示两个事物的固有速记法。
缺点是必须记住哪些变量是复数，哪些变量是普通数。

复数分为实部和虚部的数学符号使用运算符：Re() 和 Im()。例如上述复数：

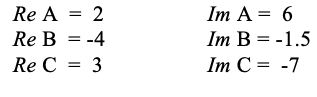
注意上式虚数部分不含 j 。

虚数运算，遵循一般数字计算：

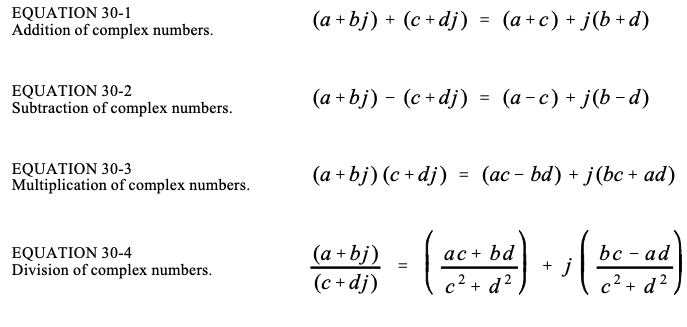
处理此类方程时需要用到两个技巧：

复数平方

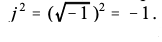
复数共轭：

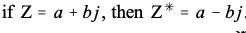
式30-4是通过将分子和分母乘以分母的复共轭得出的。

即使变量 A、B 和 C 是复数，以下属性也成立。这些关系可以通过将每个变量分解为实部和虚部并计算代数来证明。

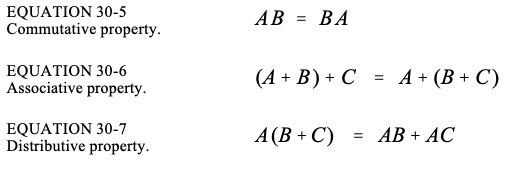
2 极坐标表示法

除了刚才描述的直角坐标表示法之外，复数还可以用极坐标表示法表示。例如，图 30-2 显示了三个极坐标形式的复数，与之前在图 30-1 中呈现的复数相同。幅度是从原点开始到复数点结束的矢量长度，而相位角是在该矢量和正 x 轴之间测量的。复数可以通过以下方程在直角坐标表示法和极坐标表示法之间转换：

极坐标到矩形的转换：

上述极坐标表达直观上难以理解，因此采用了欧拉公式进行表达：

可以通过将指数项展开为泰勒级数来证明这种关系：

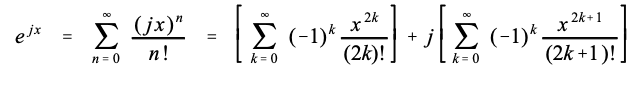
则式30-10可以用下式表示：

这种指数形式的复数是 DSP 数学的支柱。使用这种指数极坐标形式的一个强大优点是复数的乘法和除法非常简单：

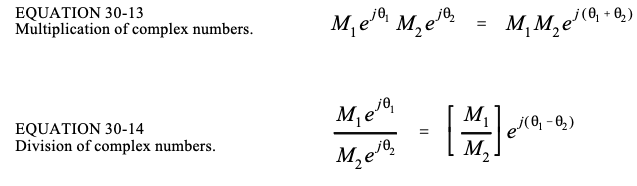
记住，Re()和Im()用于从复数中提取矩形分量，运算符Mag()和Phase()用于提取极坐标分量。比如： $A=5e^{j\pi/7}$ ，则Mag(A)=5和 $Phase(A)=\pi/7$ 。

3 通过替换使用复数

使用复数表示物理问题有两种方法：一种是简单的替换方法(substitution)，另一种是更优雅的方法，我们称之为数学等价(mathematical equivalence)。

替换采用两个实数物理参数，并将一个放在复数的实部，一个放在虚部。这允许将两个值作为单个实体（即单个复数）进行操作。经过所需的数学运算后，复数被分为实部和虚部，这又对应于我们关心的物理参数。

一个简单的例子将展示它是如何工作的。例如，想象一艘帆船被风推向一个方向，并被洋流推向另一个方向。船上产生的力是两个单独的力矢量的矢量和。这个例子如图 30-3 所示，其中两个向量 A 和 B 通过平行四边形定律相加，得到 C。

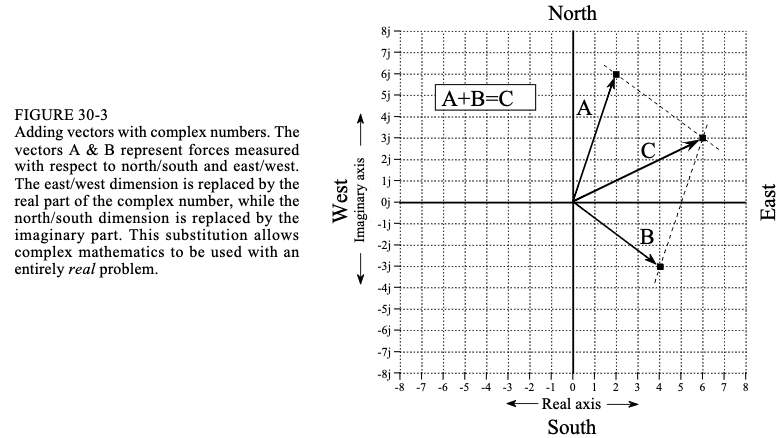
可以用复数来表示这个问题，将东/西坐标放入复数的实部，将北/南坐标放入复数的虚部。这允许、将每个向量视为单个复数，即使它由两部分组成。例如，风的力量矢量 A 的方向可能是 2 分向东和 6 分向北，表示为复数：2+6j 。同样地，可能在4部分向东和3部分向南的方向上，表示为复数： 4-3j。

如果没有复数，这个问题能解决吗？当然！复数仅提供一种形式化的方式来跟踪形成单个向量的两个分量。要记住的想法是，通过简单地将 j 添加到其中一个组件，可以将一些物理问题转换为复杂的形式。转换回物理问题无非就是去掉j。这就是替换法的本质。

4 正弦波的复数表示

复数在电子和信号处理中占有一席之地，因为它们是表示和操纵所有波形中最有用的波形（正弦波和余弦波）的紧凑方式。表示正弦曲线的传统方法是： $M\cos(\omega t+\phi)$ 或 $A\cos(\omega t)+B\sin(\omega t)$ ，分别表示极坐标和矩形符号。

使用替换，从传统的正弦曲线表示到复数的变化是简单的。以矩形形式：

式中，A等于a，B等于-b。余弦波的振幅成为复数的实部，而正弦波振幅的负值成为虚部。重要的是要理解，这不是一个方程，而只是让复数表示正弦曲线的一种方式。这种替换也可以以极坐标形式应用：

式中，M等于M， $\theta$ 等于 $-\phi$ 。极坐标符号替换留下了幅度相同，但改变了相位角的符号。

5 系统的复数表示

图 30-4 显示了使用复数表示穿过线性系统的正弦曲线的示例。尽管离散信号的处理方式相同，但将在此示例中使用连续信号。由于输入信号是正弦波，并且系统是线性的，因此输出也将是正弦波，并且频率与输入相同。

如图所示，示例输入信号具有以下常规表示形式： $3\cos(\omega t+\pi/4)$ 或等价形式 $2.1213\cos(\omega t)-2.1213\sin(\omega t)$ 或 $3e^{-j\pi/4}$ 或 $2.1213 + 2.1213 j$ ，则输出信号的表达类似，具体见下图。

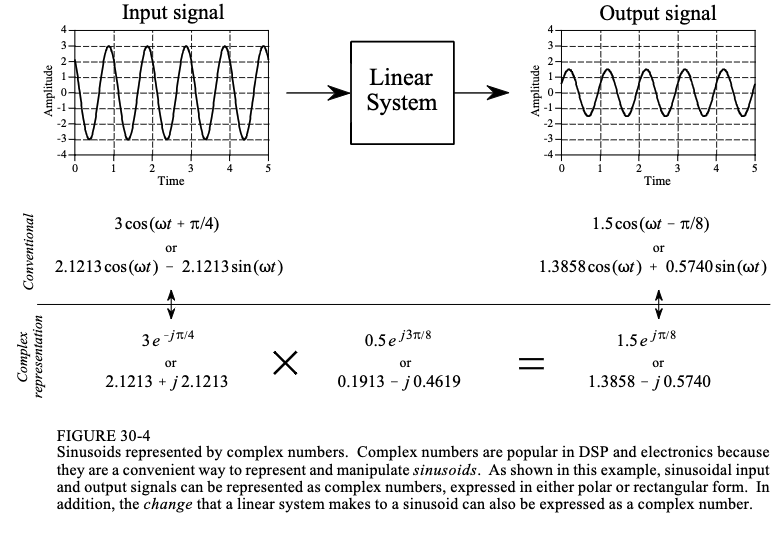
系统的特性也可以用复数来表示。复数的大小是输入输出大小之间的比率，如 $M_{out}/M_{in}$ 。同样地，复数的角度是输入输出角度差的负数，如 $-[\phi_{out}-\phi_{in}]$ 。则对于复数 $0.5e^{j3\pi/8}$ ，正弦幅度减少0.5，相位角改变 $-3\pi/8$ 。