文献阅读笔记《Spatial-temporal Forecasting for Regions without Observations》13页-编程知识

发行刊物

ABSTRACT

时空预测在交通预测、空气污染预测、人群流动预测等许多实际应用中发挥着重要作用。最先进的时空预测模型采用数据驱动的方法，并在很大程度上依赖于数据的可用性。当数据不完整时，这种模型会出现准确性问题，这在现实中很常见，因为部署和维护数据收集传感器的成本很高。

（数据不完整性）

最近的一些研究试图解决数据不完整的问题。他们通常假设某个感兴趣的区域在短时间内或在较低的位置有一些数据可用性。在本文中，我们进一步研究了在没有任何历史观测的情况下对感兴趣区域进行时空预测，以解决区域发展不平衡、传感器逐步部署或缺乏开放数据等情况。我们为该任务提出了一个名为STSM的模型。

已有研究：假设感兴趣的区域附近有数据：短期或者邻近位置

本文研究：要研究的区域没有任何历史观测数据该怎么处理，提出的模型是STSM

摘要还提到没有任何历史数据的现实原因：区域发展不平衡、传感器逐步部署或缺乏开放数据

该模型采用基于对比学习的方法，从已记录数据的相邻区域学习空间-时间模式。我们的关键见解是从与感兴趣区域相似的位置学习，我们提出了一种选择性掩蔽策略来进行学习。因此，我们的模型优于最先进的自适应模型，在交通和空气污染物预测任务中始终减少误差。

我们感兴趣的位置还没任何历史数据，但它的邻近位置有历史数据

我们的想法：

从哪学习？①从感兴趣的邻近位置学习②从与感兴趣的位置的相似位置学习
提出的学习策略：选择性掩蔽 selective masking strategy
我们的模型是sota，针对交通预测任务和空气污染任务

1 INTRODUCTION

时空预测是许多实际应用的重要组成部分，例如智能交通系统（ITS）和空气质量监测系统。当前最先进的时空预测方法是数据驱动的。他们利用顺序模型

重点研究的是：交通预测和空气质量检测（交通&空气）

开始讲现在的 sota

例如，一维卷积神经网络（CNN）[20，22，31]或递归神经网络（RNN）[16]，以捕获时间特征，以及空间模型，例如，图神经网络（GNN），其对空间关系进行建模[20，23，31]。

temporal features：时间特征

spatial：空间

CNN RNN 时间空间

GCN 空间

然而，由于传感器的高部署和维护成本以及不稳定的传输介质，数据稀缺是普遍存在的。因此，开发一个能够在没有完整历史数据的情况下进行快速预测的模型至关重要

提出问题：数据稀缺很常见（至于理由就是现实原因）

在没有任何历史数据的情况下预测

先前解决时空任务数据稀缺问题的尝试分为两类：（1）数据有时缺失[14，17，25，32，36]：由于复杂的环境和/或传感器故障，或传感器部署时间短，感兴趣位置的观测一直不完整；

散射）位置[1,30,39]：由于感兴趣的位置没有记录历史数据（例如，在这些位置没有部署传感器），因此缺少观测结果。对于后一类，最近的研究重新审视了克里格[7]。其目的是通过插入未观测位置的衍生数据，通过粗粒度观测生成细粒度记录。

注：数据缺失的两种原因：

1，data missing at times ：时间上的缺失传感器安装的时间短，采集数据不够

2，data missing at (scattering) locations：空间上的缺失就没安装采集数据的传感器

又着重说了，空间上的缺失，处理方法是生成数据

最先进的模型[30，39]采用神经网络作为解决方案。这两个类别都假设了感兴趣区域的一些可用数据，如图1（a）和1（b）所示

注：

1，现在的sota是神经网络模型

2，不管是时间上的缺失还是空间上的缺失，都假定了感兴趣的区域有一些数据

（a）时间上的缺失

（b）空间上的缺失

（c）我们解决的问题：在连续的时间和空间上数据都缺失

图1：问题设置比较。彩色地图和灰色地图分别表示观测到和未观测到的数据。我们的重点是案例（c）

现有研究没有考虑“连续”数据稀缺的情况，即没有任何数据观测的所有位置都指向一个连续的子区域（即感兴趣的区域没有可用的数据），而区域边界与有数据观测的位置相邻。

图1（c）说明了这种情况，当（1）传感器从一个地区逐渐部署到另一个地区时（香港观察到了一种这种情况[25]），（2）一些地区没有资源部署传感器（例如，上海交通拥堵数据仅覆盖核心城市地区[37]），或（3）各地区不愿意公开其数据（例如，Tom交通指数[27]没有来自中国大陆的数据）。

为了填补这一空白，我们提出了一个新问题——在没有历史数据的情况下对感兴趣区域进行时空预测。

这个新问题具有挑战性，现有的基于克里格的方法[30，39]并不能直接解决这个问题。这是因为基于克里格方法的核心思想是根据有观测的相邻位置（或时间）对没有观测的位置进行数据插值，这在我们的设置中是不可用的。

注：

克里格方法根据有观测的位置对没有观测的位置进行数据插值。

（为什么我们的问题不能用？）

例如，早期的模型IGNNK[30]将感兴趣的区域表示为图，并利用GNN进行克里格。它报告说，在我们的设置中，性能显著下降（详见第5.2节），因为当一个位置的本地邻居没有历史观测来帮助推断数据时，GNN就会变得无效。

注：

我们研究的位置：是邻居也没有历史观测的。（啊？6

最先进的克里格模型INCREASE[39]也使用了基于图的区域表示。它提前聚合了最近邻居的信息

然后使用GRU（这是一种RNN）来捕获数据的时间相关性。该模型未能利用图的全局特征，因为它只考虑最近的邻居。

我们提出了一种具有选择任务策略的时空预测模型，称为STSM，以使我们能够从与感兴趣区域相似的位置中学习，并在没有观测的情况下预测感兴趣区域。我们屏蔽子区域（靠近感兴趣区域并有历史数据）的观测数据，并训练STSM对子区域进行预测。

spatial-temporal forecasting model with a selective masking strategy 选择性掩蔽策略的时空预测模型

我的理解：

当前位置没有观测数据，邻近位置有观测数据，我们的把邻近位置的观测数据隐藏，并用STSM预测，当成训练数据

然后，在测试时，我们利用感兴趣区域和训练中使用的子区域之间的相似性来预测感兴趣区域

挖掘相似性（感兴趣＋子区域）→预测（感兴趣）

与使用随机掩蔽的现有研究[30]不同，STM结合了选择性掩蔽模块来掩蔽与感兴趣区域更相似的子区域。这种策略使STSM更容易将其预测能力从掩蔽子区域扩展到感兴趣的区域。

隐蔽策略：掩蔽子区域，什么样的子区域：与感兴趣的区域相同的区域

子区域是邻近区域把？

掩蔽了再训练，学习的模型也就可以捕捉从掩蔽到感兴趣的变化趋势

选择性掩蔽模块融合区域特征、道路网络特征和空间距离，以计算掩蔽子区域（即掩蔽位置）和感兴趣区域（即未观测位置）之间的相似性得分。相似性得分标准化为[0,1]的范围，并用作描述要屏蔽的子区域（或位置）的概率。

掩蔽位置有没有观测数据？我觉得有。

特征：①区域特征②路网特征③空间距离→计算感兴趣位置和掩蔽位置的相似性

此外，我们使用观测位置的历史数据来生成未观测位置和主题位置的伪观测值，这使得能够计算基于时间相似性的邻接矩阵，即，我们在观测位置和具有高时间相似度的未观测位置之间建立链接。这有助于识别更多相似的邻居。

总体而言，本文做出了以下贡献：

• 我们提出了一种新的时空预测任务——无历史观测区域的预报。这项任务可用于解决区域发展不平衡和缺乏开放数据的问题

我们设计了一个选择性掩蔽模块，以指导我们的模型STSM掩蔽与未观测区域具有高度相似性的观测位置，从而使STSM能够对未观测区域进行广义预测。
我们设计了一个有效的伪观测生成策略，并计算了一个基于时间邻接矩阵的onit，以帮助识别信息量更大的邻居并提高模型的学习效率

大量实验表明，就预测精度而言，我们的模型优于我们适应这一新问题的最先进模型

2 RELATED WORK（相关工作

2.1 Spatial-temporal Forecasting（时空预测

目前最先进的时空预测模型主要基于深度神经网络。DCRNN[16]引入了一种扩散卷积递归神经网络来对位置之间的空间相关性进行建模，并采用门控递归单元（GRU）来对时间相关性进行建模。GRU和其他RNN模型具有递归结构，其在模型运行时间和建模较长序列的有效性方面受到影响

为了克服这一限制，GraphWaveNet[31]利用一维时间卷积模块来捕捉时间相关性。此外，注意力机制[33]被广泛用于时空预测[6，8，10，38]。最近的一系列研究进一步将异构关系嵌入到邻接矩阵中，包括时间相似性[15，22]和嵌入

相似性[20]。一些研究[11-13,18]采用自我监督学习来增强时空模式表征。同时，DeepSTUQ[21]在预测流量时考虑了预测的不确定性。这些模型假设历史数据完全可用，当数据不完整时，学习能力会受到影响

2.2 Spatial-temporal Forecasting withIncomplete Data（不完全数据的时空预测

从数据的角度来看，现有的不完全数据时空预测方法可分为两类：时间上的数据缺失和（散射）位置上的数据丢失。

又在强调：时间上的缺失和（一些零星地点的）缺失

数据有时缺失：感兴趣位置的观测始终不完整。对于这一类别，一类主要研究集中在恶劣环境[14，17]引起的随机或连续数据丢失，例如极端天气或传输设备问题。生成对抗性网络（GAN）被应用于解决这个问题[32，36]。另一项研究[25]将迁移学习用于传感器仅在短时间内（例如10天）部署的环境

恶劣天气导致数据时间上的缺失

观测时间上的缺失solve：生成对抗网和迁移学习

（散射）位置的数据丢失：一些感兴趣的位置根本没有观测结果。考虑到这种设置的问题，即克里格[7]，旨在通过粗粒度记录来估算细粒度记录，这是为了恢复未观测到的位置的信号。高斯过程回归[29]是一种经典的解决方案，但效率低，可扩展性差。张量/矩阵补全算法[2,24,41]在大型数据集上显示出更好的效率。它们结合了低阶结构和正则化，以保持局部和全局的一致性。大多数张量/矩阵完成算法都是转导的。如果没有重新培训，他们就无法处理感兴趣的新地点。

地点上的缺失：Kriging

最近的研究[30，39]提出了归纳结构。例如，IGNNK[30]利用GNN的诱导性质和1-D CNN来记录未观察到的位置。该模型很难处理高数据丢失率，因为从邻域中几乎没有信息可供学习。INCREASE[39]采用RNN进行归纳插补。该方法使用异构关系进行更准确的估计，同时难以捕获全局时空模式。

2.3 Graph Contrastive Learning（图形对比学习

我们提出的STSM基于对比学习，特别是图形对比学习（GCL），它将对比学习应用于图形数据。对比学习的基本思想是最大限度地提高正样本之间的相似度，同时最小化负样本之间的相似性

一系列研究[34，35，42]集中于生成正样本和负样本的图扩充模块。例如，GraphCL[35]引入了四种增强方法，如节点丢弃和边缘扰动，以创建正图对。后来，GCA[42]和JOAO[34]通过考虑节点权重和边权重来改进增广策略。此外，一些研究[23，28]旨在最大化不同尺度的图输入之间的相互信息，例如节点与图。

一些研究[5，18]将GCL引入空间学习任务。例如，SARN[5]通过对比学习学习道路网络嵌入，STGCL[18]应用GCL来预测交通流量，并提供完整的数据。与STGCL不同，我们的模型可以处理完整的数据，因为所提出的选择性掩蔽模型可以基于

观察到的和未观察到的位置之间的异质相似性。

3 PROPOSED BASE MODEL（提出基本模型

我们从我们提出的模型的一个基本版本开始，命名为dSTSM RNC（图2）。我们首先定义了基本概念和我们研究的问题。然后，我们介绍了我们的基本模型及其训练和测试程序。

3.1 Concepts and Problem Statement（概念和问题描述

区域和区域图。我们将区域表示为图𝐺=(𝑉,𝐸). 图顶点的集合𝑉代表𝑁兴趣在区域中的位置（感兴趣区域的N个位置），以及图的边集𝐸表示位置之间的连接。图表𝐺有一个特征矩阵L∈R𝑁×𝐹对于位置，其中𝐹是位置特征的维度。位置的特征由两部分组成，即区域信息和道路网络信息，将在第4.1节中详细介绍。

对于每个位置𝑣𝑖∈𝑉,𝑥𝑡𝑖∈R𝐶代表观察结果𝑣𝑖在时间步长𝑡, 哪里𝐶是不同类型观测的数量，例如交通速度、PM2.5等。

观察到和未观察到的区域。区域图𝐺可以根据子区域的观测可用性，即观测区域和未观测区域，进一步划分为两个相邻的子区域。这两个区域中的位置分别被称为观测位置（即有观测）和未观测位置（如无观测）。我们使用𝑅𝑜表示包含所有且仅包含观测到的位置的区域。同样，我们使用𝑅𝑢表示包含所有且仅包含未知位置的区域。

这两个区域彼此不重叠。，𝑅𝑜∩𝑅𝑢=𝜙. 我们使用𝐺𝑜=(𝑉𝑜,𝐸𝑜)表示观察到的位置上的图形，其中𝑉𝑜⊂𝑉表示观测位置的集合，以及𝐸𝑜⊂𝐸∩ (𝑉𝑜×𝑉𝑜)表示上的边的集合𝑉𝑜. Weuse𝑁𝑜表示的大小𝑉𝑜. 类似地，我们定义了未观测位置上的图形，表示为𝐺𝑢, 然后是节点𝑉𝑢（及其大小𝑁𝑢) 和边缘𝐸𝑢在这张图上。注意，𝑁=𝑁𝑜+𝑁𝑢;十、𝑡𝐺𝑜=(𝑥𝑡1.𝑥𝑡𝑁𝑜) ∈R𝑁𝑜×𝐶表示对中观察到的位置的观察𝐺𝑜按时间步长𝑡; 和Plot X𝑡𝐺𝑢=(ˆ𝑥𝑡1.ˆ𝑥𝑡𝑁𝑢) ∈R𝑁𝑢×𝐶表示中未服务位置的估计值𝐺𝑢在时间步长𝑡

问题定义。给定一个区域图𝐺如上所述，具有位置特征L将过去的观测结果降落在观测到的位置上一段时间窗口𝑇, 我们的目标是学习一个函数𝑓预测未来未观测到的位置的值𝑇′时间步长.

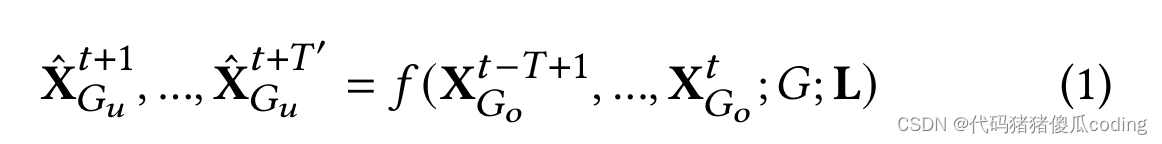
3.2 Overview of Our Base Model(我们的基本模型概述

接下来，我们提出了一个基本模型（即第5.2.2节中的STSM-RNC），该模型直接将时空建模与随机子图掩码相结合，以预测没有观测的区域，如图2所示。STSM-RNC的主要思想是学习一个模型，该模型可以通过子图来预测观测结果（例如，交通速度或PM2.5），并将这种能力扩展到未观测到的位置的预测。

我们将那些未观测到的位置的完整图表示为𝐺. 我们屏蔽的位置的子集𝐺𝑜生成maskedview𝐺𝑚𝑜（第3.3节）。根据先前的研究[9，16]，我们使用基于时间相似性的邻接矩阵和基于空间的邻接矩阵

用于空间相关性建模的邻接矩阵。为了计算未观测到的位置的时间相似性，我们首先计算所有未观测到位置的伪观测值。然后，我们使用动态时间扭曲（DTW）[3，15]来计算所有观测到的位置之间的时间相似性，以及观测到的和未观测到的地点之间的时间类似性。对于每个模型训练历元中的掩蔽位置，我们计算它们的伪观测值，并计算掩蔽位置和观测位置之间的速度相似性。

经过这些步骤，我们得到了X𝑡−𝑇+1.𝑡𝐺𝑚𝑜和X𝑡−𝑇+1.𝑡𝐺𝑚分别用于训练和测试，其中bothX𝑡−𝑇+1.𝑡𝐺𝑚𝑜和X𝑡−𝑇+1.𝑡𝐺𝑚包含中屏蔽或未观测位置的伪观测值𝐺𝑜或𝐺

我们喂养X𝑡−𝑇+1.𝑡𝐺𝑚𝑜转换为时空建模模块以生成预测结果X𝑡+1.𝑡+𝑇′𝐺𝑚𝑜（第3.4节），并将预测和基本事实之间的均方误差计算为预测损失，以优化时空模型。在模型被训练后，我们馈送X𝑡−𝑇+1.𝑡𝐺𝑚进入模型，以获得对未观测位置的预测（第3.5节

3.3 Sub-graph Masking（子图掩蔽

STSM-RNC在训练过程中学习预测掩蔽位置的值，然后将此能力扩展到在测试中预测未观测位置的值。为了模拟我们关注的没有数据观测的连续区域的设置，我们屏蔽了由每个选定位置及其1跳邻居形成的子图，而不是一组散射位置。

定义子图。观察到的位置的子图由其1跳邻居形成。我们基于空间邻接矩阵a计算位置的1跳邻居𝑠𝑔, 其由等式2定义，其中𝜖𝑠𝑔是一个超参数，并且𝑑𝑖𝑠𝑡(𝑐𝑖,𝑐𝑗)表示位置之间的距离𝑖和𝑗(𝑐𝑖和𝑐𝑗是它们的地理坐标。）出于效率考虑，我们在本文中使用欧几里得距离，尽管也可以使用道路网络距离。

一跳邻居，子图掩蔽，是我理解的意思？掩去了一级邻近邻居，保留二级邻居

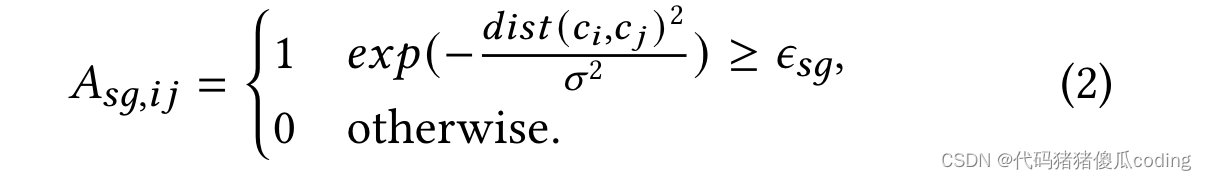
子图屏蔽。我们使用掩蔽比率𝛿𝑚以定义要屏蔽的观察位置的百分比。屏蔽的位置数预计为𝑁𝑜·𝛿𝑚. 由于每个位置的子图可能具有不同的大小，STSM-RNC迭代并随机选择一个位置，并屏蔽该位置及其1跳邻居，直到屏蔽位置的数量达到𝑁𝑜·𝛿𝑚.

3.4 Spatial-temporal Modelling（时空建模

我们的基础模型STSM-RNC的时空建模模块包含用于时间相关性建模的一维卷积网络和用于空间相关性建模的图卷积网络（GCN）。时空建模模块堆叠多个块以计算最终输出。图3显示了时空建模模块的结构，并详细说明了𝑙模块的第个块。每个区块包含一个局部相关建模模块和一个空间相关建模模块。这两个模块在每个块中是并行的。我们首先描述了时空建模模块中的输入特征和邻接矩阵。然后，我们详细介绍了时间和空间相关性建模模块

基础模型STSM-RNC的时空建模模块 =

时间相关性建模的一维卷积网络 + 用于空间相关性建模的图卷积网络（GCN）

时间建模居然用的卷积，不过一维卷积，可以的

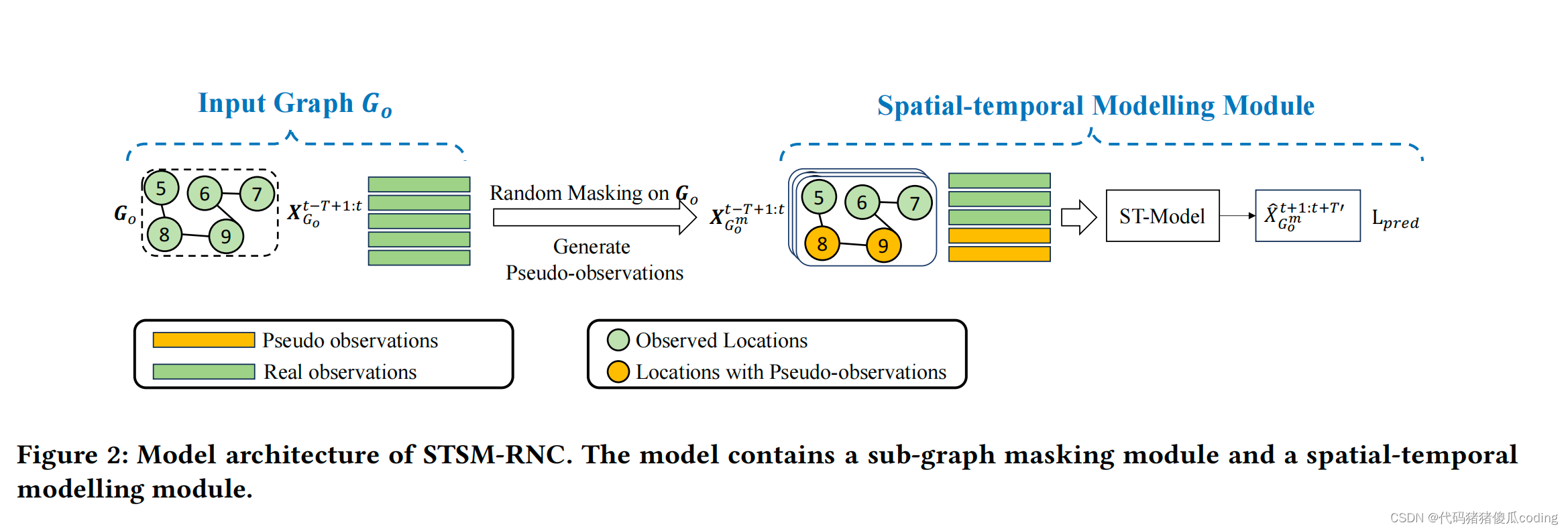
Figure 2：STSM-RNC的模型体系结构。该模型包含子图掩蔽模块和时空建模模块

图3：时空模型的结构

3.4.1.输入特征和邻接矩阵。STSM-RNC的输入特征包括观测位置的历史观测、未观测和掩蔽位置的伪观测以及用于指示一天中时间的时间注意力。此外，我们还为我们的模型中的GCN计算了两种类型的邻接矩阵。

我们计算的伪观测值𝑖-真实观测中未观测到的或推测的位置𝑥𝑡𝑖=Í𝑗∈𝑁𝑜𝛼𝑖,𝑗𝑥𝑡𝑗. 每个观测位置的权重由其对位置的空间位置决定𝑖, 如等式3所定义

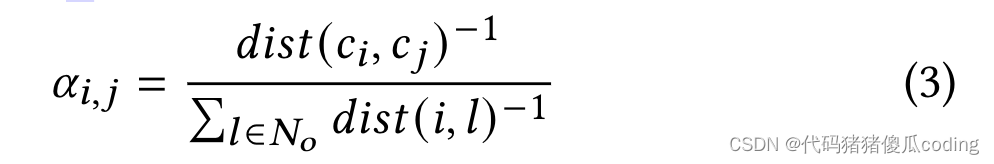
这一步骤可以基于其邻居的位置将更多信息引入未被观测或屏蔽的位置。

然后，我们建立了一个基于时间相似性的邻接矩阵。我们遵循先前的工作[15]，并采用DTW来计算时间相似性。由于伪观测可以被视为具有噪声的真实观测，因此我们只在观测位置之间以及从观测位置到未观测（屏蔽）位置建立联系（即，在GCN训练期间，未观测位置不能直接将信息发送到观测位置）。

这样，我们就避免了未观察到（掩蔽）位置的嵌入污染观察到的位置的嵌入。我们计算𝑞𝑘𝑘和𝑞𝑘𝑢最相似的观测位置对以及观测和未观测（或掩蔽）位置对。我们建立了一个基于时间相似性的邻接矩阵

在训练过程中𝑑𝑡𝑤∈R𝑁×𝑁在测试过程中），为这些位置对分配1的边缘权重，为其余位置对分配0的边缘权重。由于在每个训练时期中动态地掩蔽位置A𝑡𝑟𝑎𝑖𝑛𝑑𝑡𝑤在每个模型训练时期更新。

它这里随机化的思想还是比较有趣的，训练数据多变，每次随机mask节点

此外，我们使用时间注意力来捕捉周期性的拍频，这会显著影响时空数据的观测值，例如高峰时间。给定记录时空观测的时间间隔的长度（例如，5分钟），我们可以计算一天中的间隔数量，表示为𝑇𝑑. 现在，一天中的每个观察间隔在[0，𝑇𝑑−1].给定长度的输入𝑇, 我们计算一天嵌入的时间𝑇𝐸∈R𝑇, 其将间隔ID存储在输入时间窗口中。

例如𝑇𝐸=[0,1,2,3]表示一个输入观测序列，从一天的第一个间隔开始，到一天的第四个间隔结束。

附加时间嵌入𝑇𝐸对于模型输入，我们首先投影TE𝑡−𝑇+1.𝑡∈R𝑁𝑜×𝑇×1输入特征X𝑡−𝑇+1.𝑡∈R𝑁𝑜×𝑇×𝐶进入相同的潜在空间，然后将它们相乘，如方程4

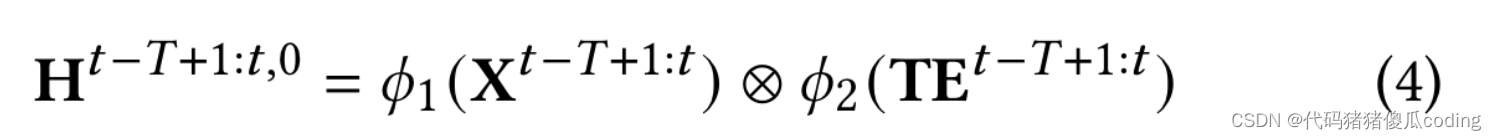
这里，X𝑡−𝑇+1.𝑡∈R𝑁𝑜×𝑇×𝐶是观测图的输入观测序列（即。𝐺𝑜或𝐺𝑚𝑜), while TE𝑡−𝑇+1.𝑡是响应时间嵌入；𝜙1（·）和𝜙2（·）是线性函数，它将输入的观测序列和时间嵌入到相同的潜在空间中进行逐元素乘法。我们现在获得功能H𝑡−𝑇+1.𝑡,0∈R𝑁𝑜×𝑇×𝐶′, 作为时空模型的输入。

该说不说，这数学符号的表达真的很规范

3.4.2时间相关建模.

1-D卷积神经网络在时间特征建模方面表现出强大的性能。我们采用一维扩张卷积神经网络来嵌入时间特征。为了便于演示，我们简化了时空模型第一层的输入特征的表示法

H巴拉巴拉的那个是上一层的输出；

H𝑙𝑡𝑐𝑛∈R𝑁×𝑇×𝐶′,𝑙=1,2, . . .,𝐿第𝑙层的一维时间卷积网络的输出；

*𝑑𝑙表示堆叠一维相关时间卷积网络，其中𝑑𝑙𝑗表示指数膨胀率，𝑑𝑙𝑗=2.𝑗.

为了保持时间序列表示的维数相同，我们使用零填充。

作用𝜎（·）是激活函数（例如ReLU或者sigmoid

3.4.3空间相关性建模。我们使用图卷积网络（GCN）来对空间相关性进行建模。GCN的基本思想是聚合来自邻居的特征：

式中eA=A+I，andeD是对角矩阵。矩阵Z∈R𝑁×𝐶是输入图节点的特征。矩阵W∈R𝐶×𝐶′包含模型要学习的参数，其中𝐶是输入维度和𝐶′是输出维度。接下来，我们定义具有两个平行GCN的GCN层，记作GCNL

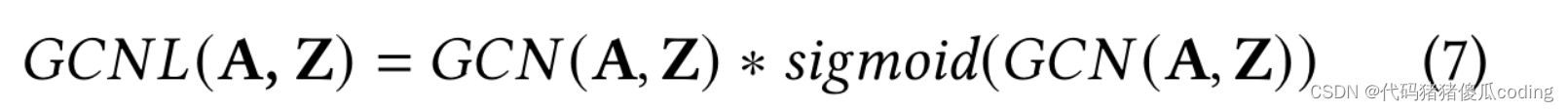
什么？eg7在哪里提到了？

我们堆叠GCN层来构建GCN块。每个GCN层的输出是下一个GCN层的输入，如等式8所示，其中𝑞∈ 1.𝑘]. 第一层输入为H𝑙,𝑡−𝑝,0𝑔𝑐𝑛,𝑟=H𝑙−1.𝑡−𝑝,哪里𝑝∈ [𝑇−1,0]和𝑟∈ {𝑠,𝑑𝑡𝑤}表示两种类型的邻接矩阵（即基于空间邻近性的矩阵和基于空间相似性的矩阵）

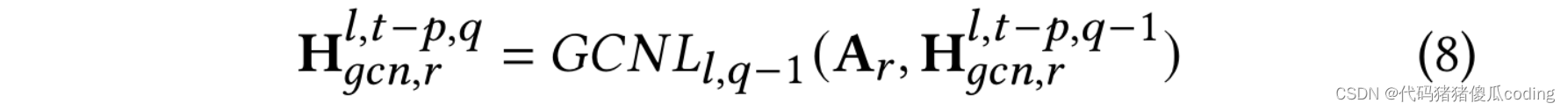
我们使用𝑚𝑎𝑥（·）聚合GCN层的输出以获得第𝑙-th个GCN块的输出

就是说，你真的不觉得这个公式有点子复杂嘛哈哈哈哈笑薯我了

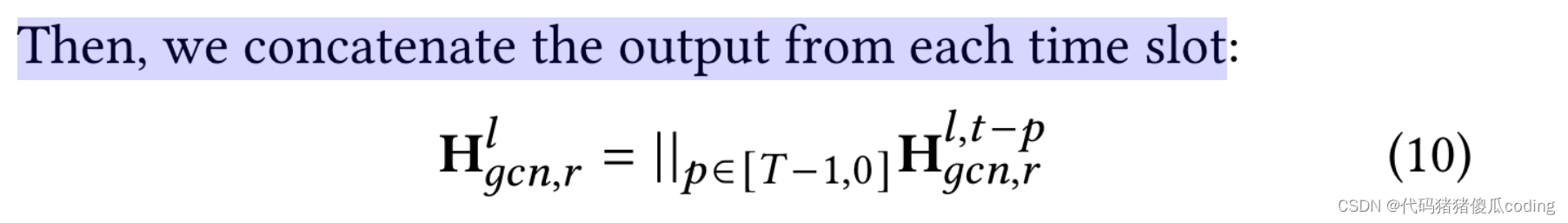
然后，我们关注每个时间间隙的输出。

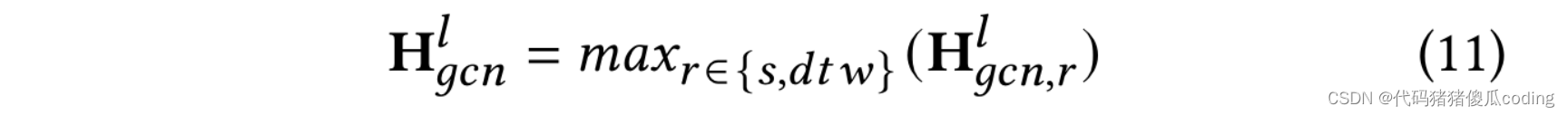
之后，我们使用𝑚𝑎𝑥（·）再次聚合对应于两个不同邻接矩阵的输出，如等式11所示，以获得的第𝑙-th层输出。

我们遵循先前的研究[9，16]，并采用具有不同阈值的等式2-𝜖𝑠计算基于空间的邻接矩阵。同时，我们遵循另一项工作[15]，采用DTW[3]来计算A𝑑𝑡𝑤, 如前所述。

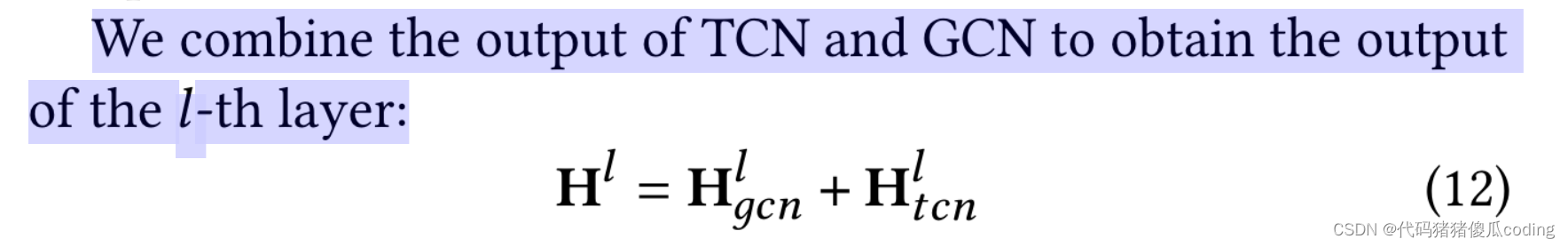
我们将TCN和GCN的输出组合起来，以获得第l层的输出。

TCN哪里出现了？

组合输出形式，可以的。四则远算还有权重是个问题

最后，我们得到输出H𝑡+1.𝑡+𝑇′,𝐿在𝐿-第h层遵循上述步骤和线性函数投影H𝑡+1.𝑡+𝑇′,𝐿到较低的维度（如等式13所示）

在这里𝜙3和𝜙4为线性函数，以及𝜎是一个激活函数𝑡+1.𝑡+𝑇′∈R𝑁𝑜×𝑇′×𝐶表示预测值

3.5 Model Training and Testing（模型训练和测试

模型训练：我们获得预测值𝑡+1.𝑡+𝑇′𝐺𝑚𝑜论图形观𝐺𝑚𝑜这是通过子图掩码生成的。然后，我们计算预测值之间的均方误差𝑥𝑡+𝑝′𝑖以及基本事实𝑥𝑡+𝑝′𝑖作为预测损失（Eq 18

模型测试：在模型测试过程中，我们首先计算未观测到的位置的伪观测值，并让图𝐺用伪观测𝐺𝑚. 然后，我们利用这些伪观测建立了基于时间相似性的邻接矩阵。之后，我们提供特征X𝑡−𝑇+1.𝑡𝐺𝑚∈R𝑁×𝑇×𝐶

feed翻译成提供，或者理解成输入特征

到训练的模型中，以产生预测的观测值𝑡+1.𝑡+𝑇′𝐺𝑚对于未观测到的位置。

4 PROPOSED FULL MODEL（提出的完整模型

第3节介绍了我们的基本模型。在本节中，我们将介绍两个模块——选择性掩蔽模块和集中学习模块，以增强我们提出的模型性能。这两个模块与我们的基本模型STSM-RNC一起形成了我们的完整模型STSM。图4显示了它的总体结构。

回想一下，我们的核心思想是学习一个模型，该模型可以将掩蔽位置的预测能力扩展到未观测位置。

STSM的三方面构成：

selective masking module（选择性掩码模块）挺会形容。
contrastivelearning module（对比学习模块）
STSM-RNC

STSM在全图上性能的可推广性𝐺取决于中屏蔽位置之间的相似性𝐺𝑚𝑜以及未观测到的地点𝐺. 为了掩盖与未观测位置具有更高相似性的位置，我们提出了一个选择性掩蔽模块，以增强子图掩蔽，利用观测位置和未观测位置之间的相似性来帮助预测未观测位置的值（例如，交通速度或PM2.5）

两个数据集：交通数据集&空气质量数据集

该模块利用区域信息和位置周围的道路网络信息以及空间距离来计算位置的掩蔽概率。我们在每个模型训练中基于这样的概率来掩蔽位置，以生成𝐺𝑚𝑜. 该模块可以指导STSM学习预测与未观测到的位置具有更高相似性的位置的值，从而增强模型的通用性。

说的是掩码模块

掩码概率：区域信息 + 路网信息 + 空间距离

我们进一步设计了一个对比学习模块，该模块采用基于图对比学习的方法，构建了图的两个视图——一个视图包含完整的空间-时间数据（原始视图），另一个视图则包含不完全的空间-时间数据（扩充视图）。具有完整数据的视图用于指导对具有不完整数据视图的预测。

增强视图𝐺𝑚𝑜由选择性掩蔽模块生成。使用对比学习，我们学习了一个模型，它为两个图视图生成相似的预测。然后将训练后的模型应用于全图𝐺以对未观测到的位置进行预测。

我们喂养X𝑡−𝑇+1.𝑡𝐺𝑜和X𝑡−𝑇+1.𝑡𝐺𝑚𝑜进入所提出的时空建模模块（如第3.4节所述），以获得图形表示Z𝑡+𝑇′𝐺𝑜和Z𝑡+𝑇′𝐺𝑚𝑜用于对比学习和生成预测结果X𝑡+1.𝑡+𝑇′𝐺𝑚𝑜.

当模型被训练时，我们馈送X𝑡−𝑇+1.𝑡𝐺𝑚以获得未观测位置的预测（第3.5节)

4.1 Selective Masking（选择性掩码

STSM在训练过程中学习预测掩蔽位置的值，然后在测试中扩展这一能力以预测未观测位置的值。直观地说，掩蔽位置和未观测位置之间的相似性越高，训练的模型就越容易对未观测到的位置进行预测。我们计算这些1-跳子图（在第3.3节中定义）和未观测区域之间的相似性。之后，我们使用我们提出的选择性掩蔽模块来引导STSM掩蔽由观测位置的子图形成的子区域，这些子图与未观测区域最相似。从启发性的角度来看，这种策略可以为未观察到的区域中的位置带来更准确的预测结果。

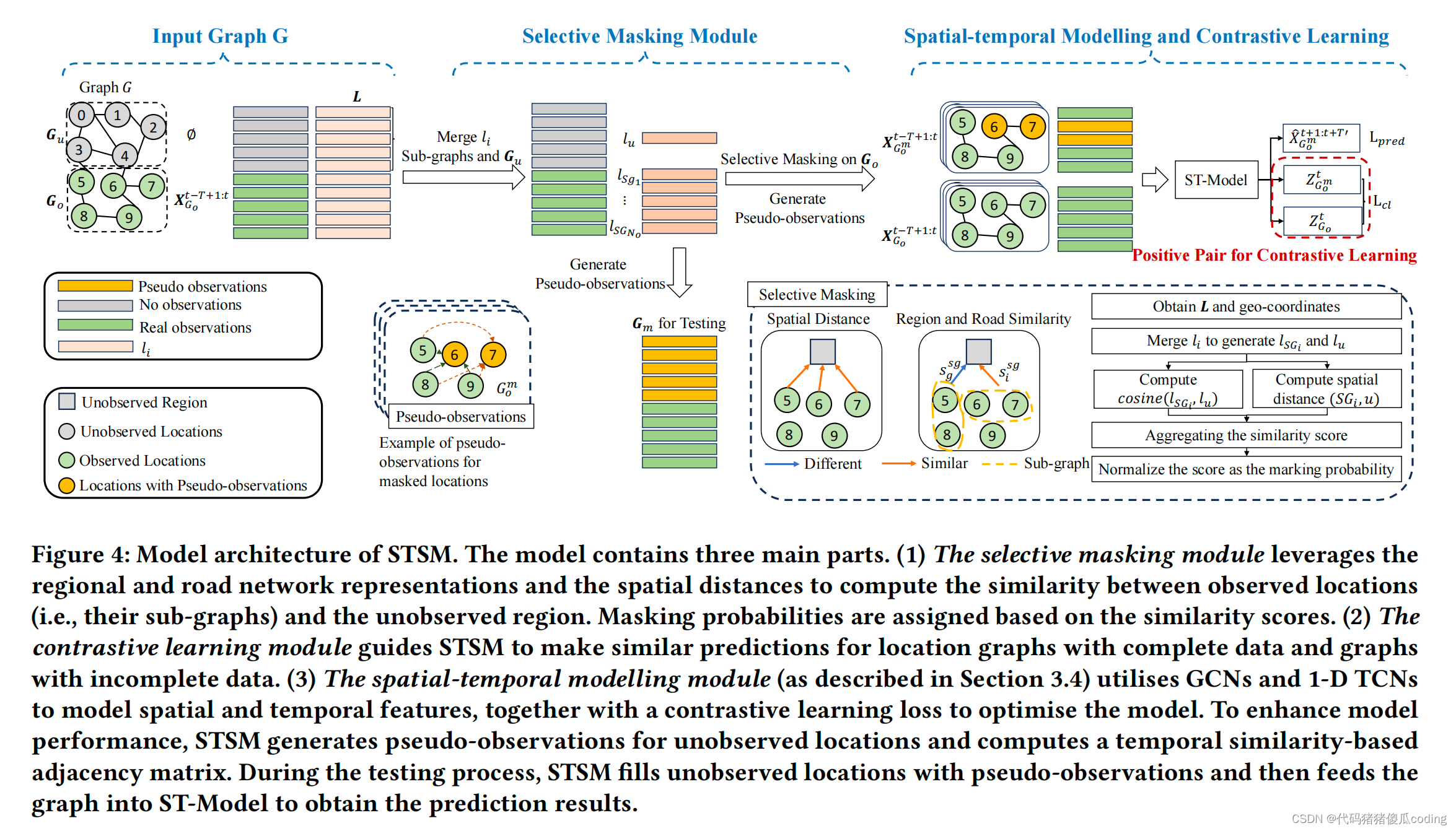图4：STSM的模型架构。该模型包括三个主要部分。

Model architecture of STSM. The model contains three main parts.

（1）选择性掩蔽模块利用区域和道路网络表示以及空间距离来计算观察到的位置（即，它们的子图）和未观察到的区域之间的相似性。基于相似性得分来分配掩蔽概率。

(1) The selective masking module leverages the regional and road network representations and the spatial distances to compute the similarity between observed locations (i.e., their sub-graphs) and the unobserved region. Masking probabilities are assigned based on the similarity scores.

（2）对比学习模块指导STSM对具有完整数据的位置图和具有不完整数据的图进行相似的预测。(2) The contrastive learning module guides STSM to make similar predictions for location graphs with complete data and graphs with incomplete data.

（3）时空建模模块（如第3.4节所述）利用GCN和一维TCNsto对空间和时间特征进行建模，并结合对比学习损失来优化模型。为了提高模型性能，STSM为未观测到的位置生成伪观测值，并计算基于时间相似性的邻近矩阵。

(3) The spatial-temporal modelling module (as described in Section 3.4) utilises GCNs and 1-D TCNs to model spatial and temporal features, together with a contrastive learning loss to optimise the model. To enhance model performance, STSM generates pseudo-observations for unobserved locations and computes a temporal similarity-based adjacency matrix. During the testing process, STSM fills unobserved locations with pseudo-observations and then feeds the graph into ST-Model to obtain the prediction results.

6，我有点好奇，它用啥画的图，数学符号的表示，技术路线都比较清晰。

子图表示。为了测量子图和由未观测位置形成的区域之间的相似性，我们需要首先计算每个观测位置的子图的表示。我们用三个组件形成这样的表示（即嵌入）：

（1）兴趣点（POI）特征。对于每个观察到的位置，我们绘制一个以半径为中心的圆𝑟（系统参数），并从OpenStreetMap[19]收集电路内的所有POI。我们将POI分类为Γ类（参见表1）。

子图嵌入的POI特征组件，表示为𝑙𝑝𝑜𝑖𝑖∈Γ，是保持每个类别的POI的计数的一个向量。我们进一步从OpenStreetMap[19]中获得圆形区域中建筑的层数和公园的面积，以表示子图的繁荣程度，如𝑙𝑠𝑐𝑎𝑙𝑒𝑖∈例如，具有60级建筑的子图（即局部区域）比仅具有4级建筑的子图更繁荣。

我们连结𝑙𝑝𝑜𝑖𝑖和𝑙𝑠𝑐𝑎𝑙𝑒获得子图的区域嵌入，表示为𝑙𝑟𝑒𝑔𝑖𝑜𝑛𝑖=[𝑙𝑝𝑜𝑖𝑖||𝑙𝑠𝑐𝑎𝑙𝑒𝑖] ∈RΓ+，其中||表示连结

（2）路网特点。我们选择该位置最近的道路。为了表示与子图相对应的道路网络，我们使用4维向量𝑙 𝑟𝑜𝑎𝑑𝑖∈R4（终于看懂了一个数学符号！）其中的维度有：高速公路等级、最大速度、is_oneway和车道数

最后，我们将位置的区域表示和拓扑网络表示连接起来𝑖以形成其嵌入。，𝑙𝑖=[𝑙𝑟𝑒𝑔𝑖𝑜𝑛𝑖||𝑙𝑟𝑜𝑎𝑑𝑖] ∈Γ+5。位置子图的嵌入𝑖, 记为𝑙𝑆𝐺𝑖, 被计算为子图中所有位置的嵌入的平均嵌入。，𝑙𝑆𝐺𝑖=1.𝑉𝑆𝐺𝑖|Í𝑗∈𝑉𝑆𝐺𝑖𝑙𝑗.

子图和未观测区域之间的相似性。按照同样的策略，我们可以计算一个嵌入ding𝑙𝑢通过对所有未观测到的位置的em层理取平均值来获得完整的未观测到区域。然后，位置子图之间的相似性𝑖并且未观测区域被计算为两个嵌入的余弦相似性。，即𝑠𝑔𝑖=𝑐𝑜𝑠𝑖𝑛𝑒(𝑙𝑆𝐺𝑖,𝑙𝑢)), 与空间接近度相结合𝑠𝑝𝑠𝑔𝑖=1.𝑑𝑖𝑠𝑡(𝑐𝑖,𝑐𝑢)指导掩蔽过程。

我们计算所有子图和未观察区域之间的嵌入相似性，表示为𝑆𝑠𝑔=[𝑠𝑠𝑔1.𝑠𝑠𝑔𝑁𝑜], 和空间接近度𝑆𝑃𝑠𝑔=[𝑠𝑝𝑠𝑔1.𝑠𝑝𝑠𝑔𝑁𝑜]

子图屏蔽。我们使用掩蔽比率𝛿𝑚以定义待掩蔽的观察到的位置的百分比。由于每个位置的子图可能具有不同的大小，我们计算所有子图的平均大小，表示为𝛿𝑠=1.𝑁𝑜Í𝑖∈𝑁𝑜|𝑉𝑆𝐺𝑖|.如果我们屏蔽具有相同概率的子图𝛿𝑚𝑠=𝛿𝑚/𝛿𝑠,屏蔽的位置的最终数量预计为𝑁𝑜·𝛿𝑚.由于我们想要使用相似性来引导STSM来屏蔽ob服务的位置，

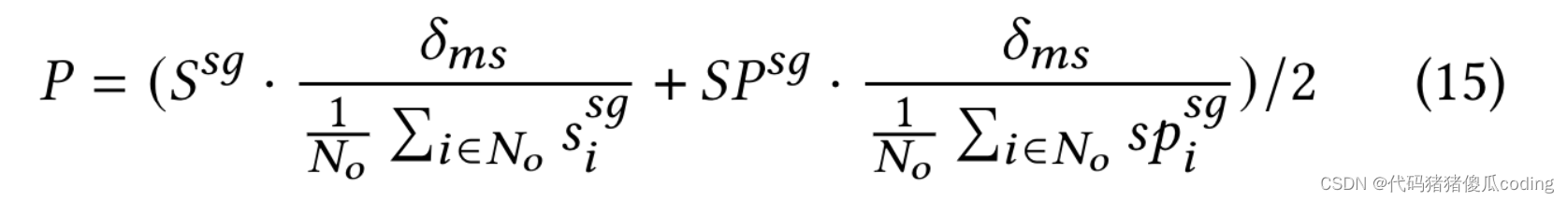
我们把相似之处结合起来𝑆𝑠𝑔, 空间近似性𝑆𝑃𝑠𝑔以及子图掩蔽比𝛿𝑚𝑠以计算每个位置的掩蔽概率，如等式15所示。该方程归一化𝑆𝑠𝑔和𝑆𝑃𝑠𝑔让他们有贡献。

子图的大小和图的大小𝐺影响价值𝑝𝑖∈𝑃. 当它们很大时，𝑝𝑖可以变得非常小，使得所有子图都具有非常接近的概率值。为了解决这个问题，我们只保留顶部-𝐾最相似的子图，并将其余子图的相似性值设置为0，其中𝐾是一个超参数。

这种策略减少了图中可以屏蔽的子图的数量。然后，我们掩盖

基于掩蔽概率的子图更类似于未观测区域𝜌𝑖, 来自伯努利分布𝜌𝑖∼𝐵𝑒𝑟𝑛(𝑝𝑖)生成具有遮罩位置的图形(𝐺𝑚𝑜)

4.2 Graph Contrastive Learning（图形对比学习

根据第4.1节，我们使用𝐺𝑜（即，具有完整数据的图）以生成图𝐺𝑚𝑜具有不完整数据（即具有掩蔽位置的图形）。图表𝐺𝑚𝑜可以被视为𝐺𝑜具有扰动（即，𝐺𝑚𝑜和𝐺𝑜是观测图的两个视图，以及𝐺𝑚𝑜是的扩充𝐺𝑜). 指导STSM在𝐺𝑚𝑜和𝐺𝑜, 我们将对比学习应用于图的这两个视图的训练过程中。

STSM采用图级对比学习。我们使用原始图𝐺𝑜来解释我们的图表示生成步骤。首先，[X]𝑡−𝑇+1.𝐺𝑜, . . .,十、𝑡𝐺𝑜]被输入到时空模型中（如第3.4节所述），以生成每个时隙的输出，表示为H𝑡:𝑡+𝑇′,𝐿𝐺𝑜, 哪里𝐿是时空模型中的层数。

然后，STSM获取最后一个时间步长的时空模型的最后一层输出，即H𝑡+𝑇′,𝐿𝐺𝑜, 以获得图的表示Z𝑡+𝑇′𝐺𝑜. 将所有位置的表示分解，并将其投影到一个新的潜在空间中，公式化为等式16，其中𝜙（·）是alinear函数。我们按照相同的步骤生成表示Z𝑡+𝑇′𝐺𝑚𝑜属于𝐺𝑚𝑜

一批𝑀在训练时对输入时间窗口进行采样，形成2𝑀表示，其中（Z𝑡+𝑇′𝐺𝑜,Z𝑡+𝑇′𝐺𝑚𝑜)是一个正对（即图𝐺𝑜和图形𝐺𝑚𝑜从同一时间槽形成正对）。负巴黎是由另一个产生的𝑀−1批次中的图形（即图形𝐺𝑜和图形𝐺𝑚𝑜从一批中的不同时隙形成负对），表示为（Z𝑡+𝑇′𝐺𝑜,Z𝑡′+𝑇′𝐺𝑚𝑜). 我们采用对比损失来最大化样本对的相互信息

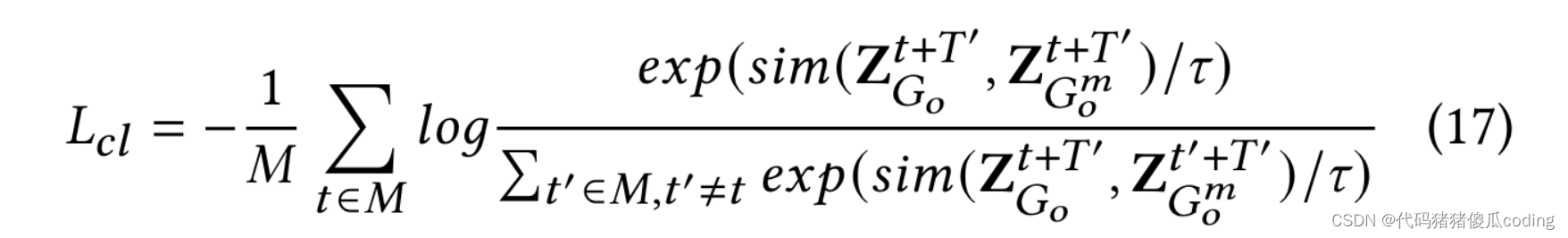
优化STSM的最终损失函数为：

𝜆是一个平衡预测损失和对比学习损失的系数。

5 EXPERIMENTS（实验

5.1 Experimental Setup（实验设置

5.1.1数据集。我们在三个高速公路交通数据集、一个城市交通数据集和一个空气质量数据集上进行了实验。

PEMS湾[16]包含2017年1月至6月期间从加利福尼亚州湾区高速公路上的325个传感器收集的交通速度数据

PEMS-07[4]包含洛杉矶高速公路上传感器收集的交通速度数据。根据之前的一项研究[20]，我们随机抽取了400个传感器，并将其在2022年9月至12月期间收集的数据作为数据集。

PEMS-08[4]包含加利福尼亚州圣贝纳迪诺地区高速公路上传感器收集的交通速度数据。同样，我们使用了2022年9月至12月期间400个随机采样传感器收集的数据。

墨尔本包含2022年7月至9月期间澳大利亚墨尔本市182个传感器从AIMES项目收集的交通速度数据[26]

AirQ[40]包含2014年5月至2015年4月期间由中国两个相邻城市北京和天津的63个传感器收集的污染物浓度数据（PM2.5）。

从PEMS收集的所有交通记录都是在5分钟窗口内给出的，即每天288个时隙，而墨尔本数据集的交通记录是在15分钟窗口内提供的，即每日96个时隙。空气质量记录以小时为单位，即每天24个时段。表2总结了数据集的统计数据，图5显示了所有数据集之间的传感器分布。用于选择性掩蔽的区域和道路网络信息从OpenStreetMap[19]中获得。

在基线工作[30]之后，我们使用过去两个小时的记录来预测接下来的两个小时，即。，𝑇=𝑇′=2.ℎ𝑜𝑢𝑟𝑠在用于交通数据集的等式1中。在另一项基线工作[39]之后，我们使用过去24小时的记录来预测接下来的24小时，即。，𝑇=𝑇′=24ℎ𝑜𝑢𝑟𝑠在空气质量数据集的等式1中。

我们以4:1:5将每个数据集分为三组进行训练、验证和测试，其中每组中的位置彼此相邻。请注意，训练集中和验证集中的位置被视为观察到的位置，而测试集中的位置则被视为未观察到的地点。数据集分割是基于空间的，根据传感器的地理坐标将传感器水平或垂直划分为三组。

对于每个数据集，我们创建四个不同的分割，并报告每个数据集的平均性能。我们使用前70%的训练时间和后30%的测试时间记录的数据。图6显示了PEMS Bay上的数据集划分及其时间划分。

5.1.2竞争对手。

我们提出的问题没有现有的模型。我们采用以下自适应模型与我们提出的模型STSM进行实证比较：

• GE-GAN[32]是一种基于生成对抗性网络（GAN）的转导数据插补方法，利用生成器生成估计值，并利用判别器对真实值和生成值进行分类。

• IGNNK[30]是一种用于时空克里格的归纳图神经网络。

• INCREASE[39]是一个基于GRU和时空克里格技术的归纳图表示学习网络

5.1.3实施细节。

我们使用源代码中基线模型的默认设置。基线模型是为数据插补而提出的，而我们的目标是预测。

我们将它们的地面实况改变为未来的时间窗口，而不是过去的时间窗口来训练模型并获得预测。

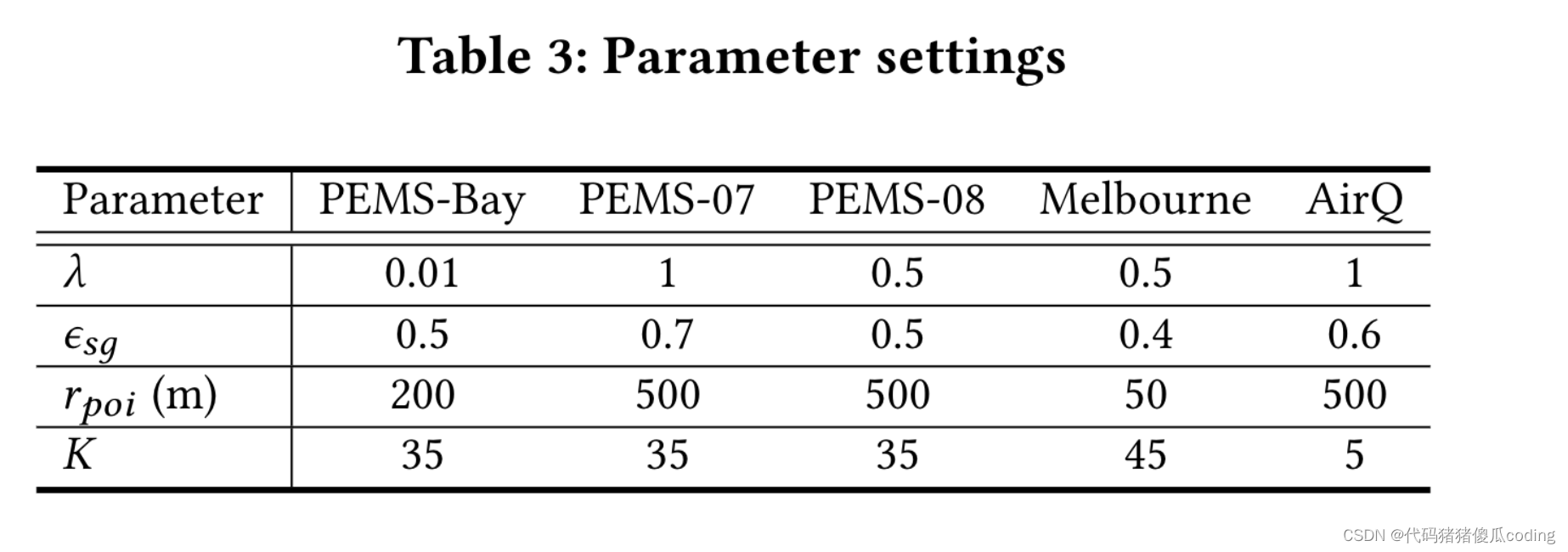
我们使用Adam优化器训练我们的模型，学习率从0.01开始。批量大小为32。对于我们模型中的超参数，𝜏为0.5，𝜎𝑚为0.5，𝜖𝑠为0.05并且𝑞𝑘𝑘和𝑞𝑘𝑢设置为1。我们将其他模型超参数的细节（即。，𝜆,𝜎𝑠𝑔,𝑟𝑝𝑜𝑖和𝐾) 如表3所示。这些参数值是通过验证集上的网格搜索获得的，除了𝑟𝑝𝑜𝑖其仅基于子图和未观察到的区域之间的相似性（即。𝑆𝑠𝑔).

此外，参数值可以在具有相似分布的数据集之间共享，例如，当只有感觉的数量或密度发生变化时（参见表6和表7）。在实验中，我们对基于空间的矩阵使用了不同的阈值𝐴𝑠和𝐴𝑠𝑔.图7显示了PEMS Bay上的两个邻接矩阵。实验在NVIDIA特斯拉V100 GPU上运行。

我们采用四种常用的指标来评估模型性能，包括均方根误差（RMSE）、平均绝对误差（MAE）、平均百分比误差（MAPE）和R平方（R2）。前三个测量预测误差，而R2测量模型预测结果与仅使用平均观测值作为结果相比有多好[39]

5.2 Experimental Results（实验结果

我们首先将我们的模型的总体性能与基线方法进行比较。然后，我们报告了消融研究的结果，以验证STSM中每个模块的有效性。最后，我们研究了参数对测试模型稳健性的影响。

5.2.1模型性能比较。

我们首先将STSM与基线方法进行比较。

（1）总体结果

表4总结了总体性能结果。STSM及其变体，包括基本模型STSM RNC（详见第5.2.2节），在所有四个数据集上都优于所有竞争对手，但AirQ上的MAPE测量除外。

GE-GAN是一种利用基于图形嵌入的相似位置为未观测位置生成值的转导方法。当大面积存在许多未观测到的位置时，很难找到相似的位置，导致预测精度很低。在墨尔本市等城市地区，GE-GAN的表现优于其他两个基线模型，因为该地区相对较小。

IGNNK是一个归纳模型，使用GNN对空间相关性进行建模，使用一维卷积神经网络获取时间相关性。它在我们的任务中很困难，因为连续位置的数据丢失使GNN很难获得空间相关性模式。尽管它在AirQ上的MAPE略低，但在该数据集上，它的MAE和RMSE仍然比我们的模型STSM大得多。这可以解释

较小的观测值出现较低的MAE，而较大的观测值则出现较高的MAE

表4：整体模型性能。“↓” 和↑”) 指示值越低（和越大）越好。最佳基线结果用下划线表示，所提出的STSM模型的最佳结果用粗体表示。改进计算所提出的模型的最佳变体与最佳基线模型相比所产生的误差，其中N/A表示由于基线方法上的负测量值，无法计算改进结果

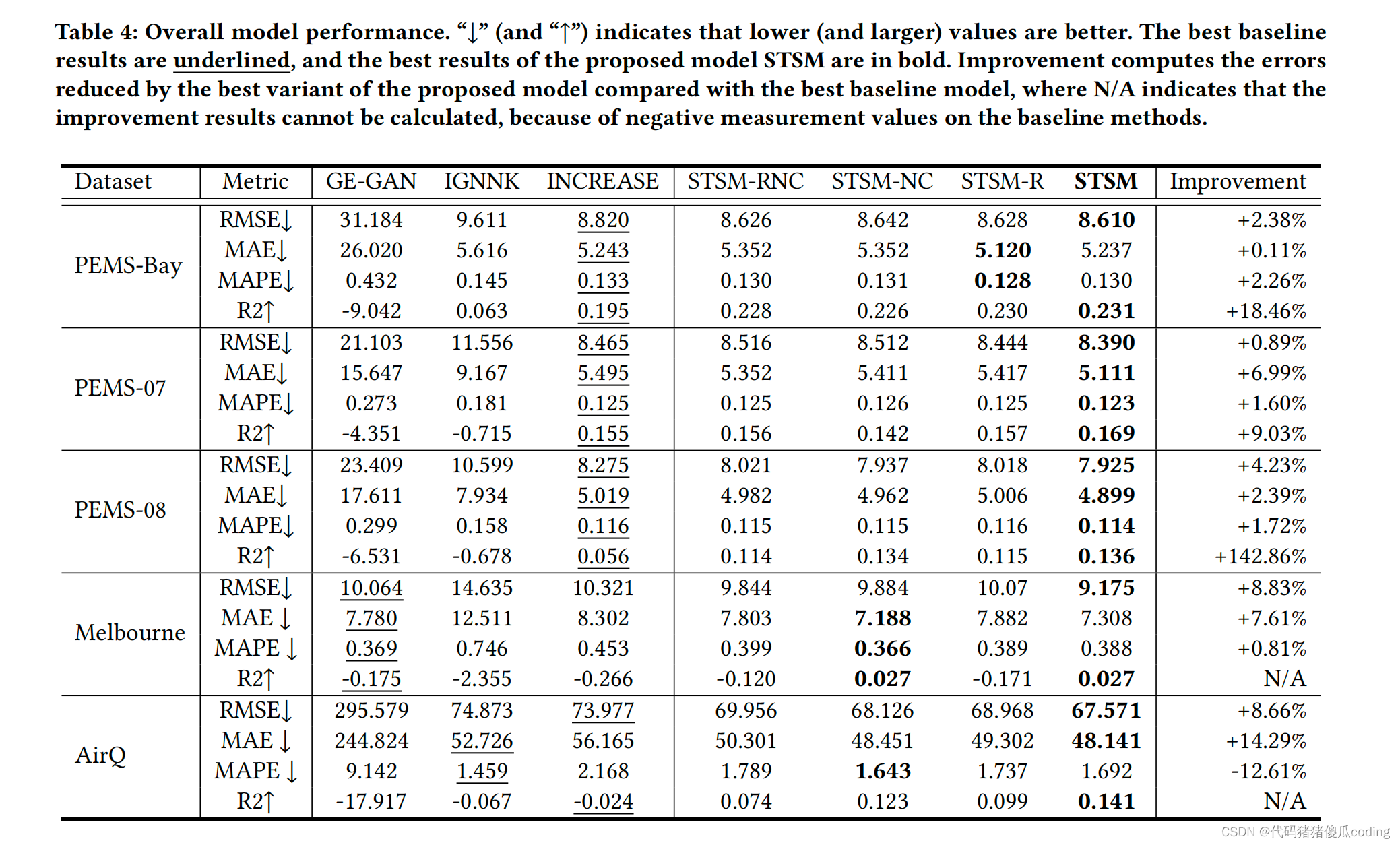
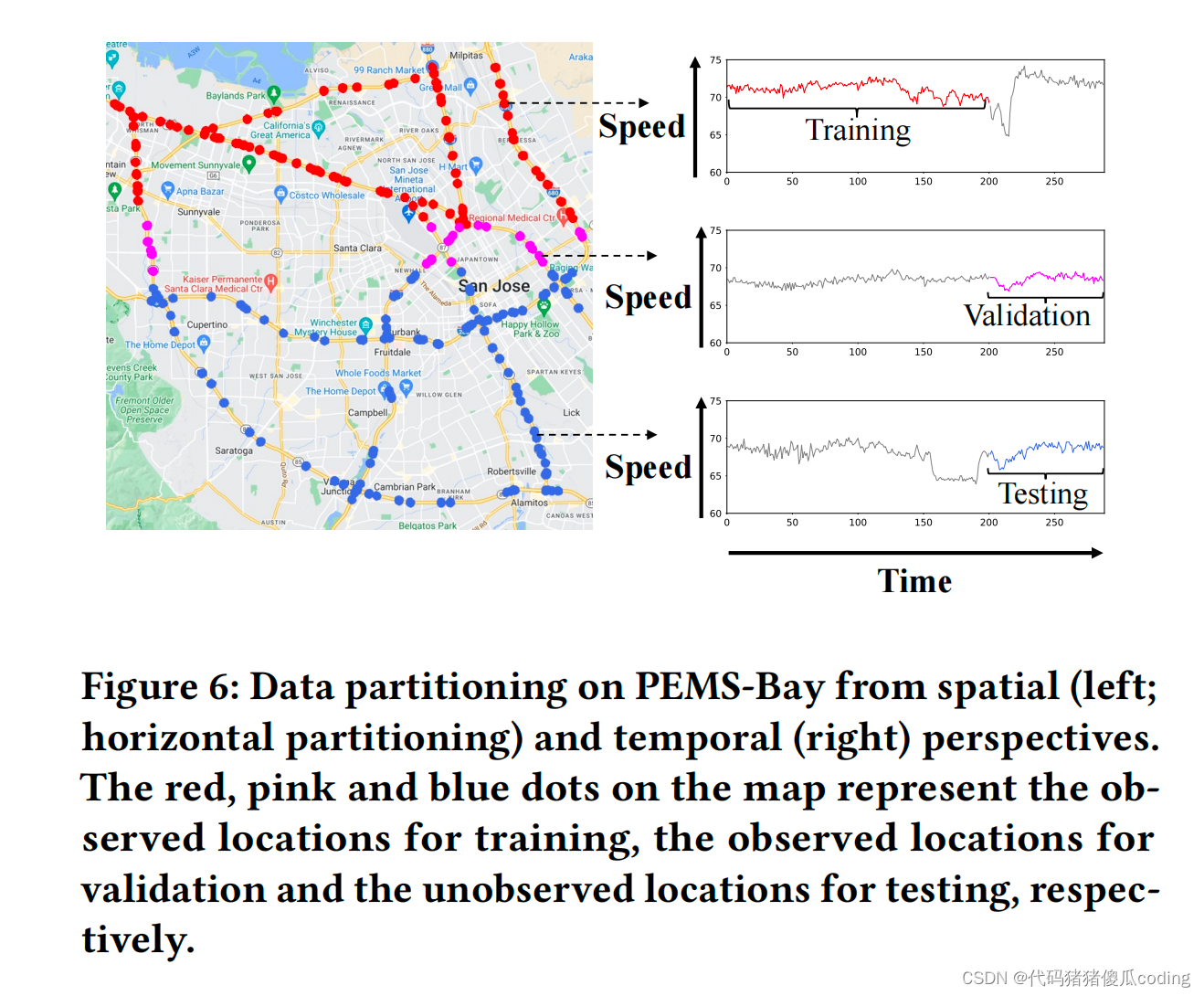
图6：从空间（左；水平分区）和时间（右）角度对PEMS湾进行数据分区。地图上的红色、粉色和蓝色圆点分别代表观察到的训练位置、观察到的验证位置和未观察到的测试位置。

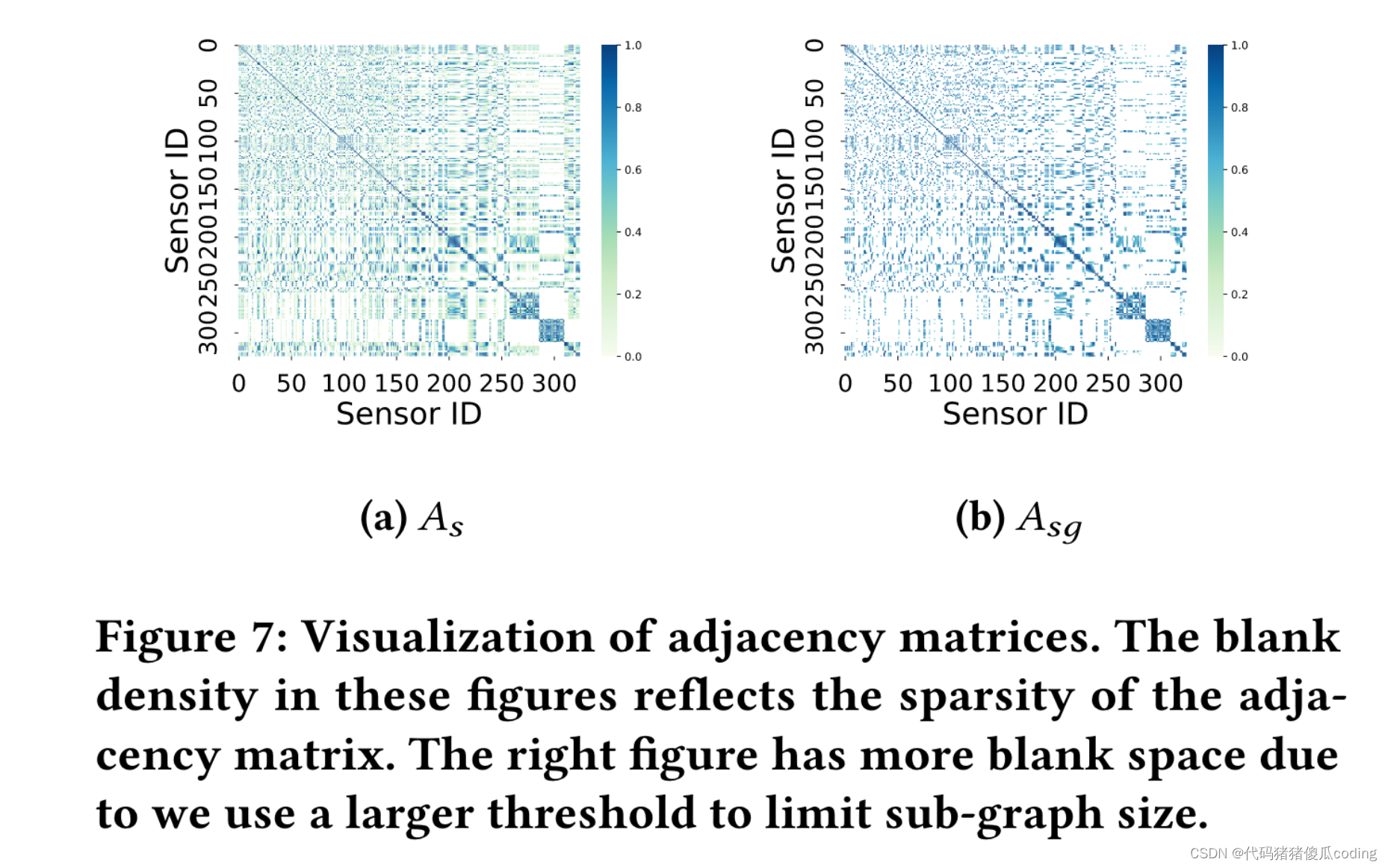
图7：邻接矩阵的可视化。这些图中的空白密度反映了邻接矩阵的稀疏性。右图有更多的空白空间，因为我们使用了更大的阈值来限制子图的大小

INCREASE是最先进的时空克里格模型，它学习异构的空间关系和不同的时间模式，在基线模型中表现出最好的性能。然而，它仍然优于我们的STSM模型。我们的模型在AirQ数据集上将预测误差减少了14%，在PEMS-08数据集上使R2增加了142%

6 CONCLUSIONS AND FUTURE WORK（结论和未来的工作

We proposed a new task - spatial-temporal forecasting for aregion of interest without historical observations while this re-gion’s adjacent region has such data. We design a novel modelnamed STSM for the task. We propose a selective masking mod-ule based on region, road network and spatial distance features.This module can guide STSM to mask locations in the adjacentregion that have higher similarity with those in the region ofinterest, which is beneficial for extending the forecasting capa-bility of STSM to the region of interest.

我们提出了一个新的任务——在没有历史观测的情况下对感兴趣的区域进行时空预测，而该区域的相邻区域有这样的数据。我们为该任务设计了一个新的模型STSM。我们提出了一种基于区域、道路网络和空间距离特征的选择性掩蔽模型。该模块可以引导STSM屏蔽相邻区域中与感兴趣区域中相似性较高的位置，有利于将STSM的预测能力扩展到感兴趣区域。

相反，STSM利用对比学习来提高模型预测的有效性。在包括交通数据和空气质量数据在内的真实世界数据集上的实验结果表明，STSM在预测精度方面始终优于最先进的模型。这一优势得益于（1）选择性掩蔽模块，它引导模型掩蔽与感兴趣区域更相似的区域，从而更好地概括预测；（2）对比学习，它提高了模型对不完整数据的准确性；（3）基于时间相似性的邻接矩阵计算，它增强了GCN的学习能力，允许消息从观察到的位置传递到未知的位置。