💯 博客内容:【茶话数据结构】查找最短路径——Dijkstra算法详解
😀 作 者:陈大大陈
🦉所属专栏:数据结构笔记
🚀 个人简介:一个正在努力学技术的准前端,专注基础和实战分享 ,欢迎私信!
💖 欢迎大家:这里是CSDN,我总结知识和写笔记的地方,喜欢的话请三连,有问题请私信 😘 😘 😘
目录
题记
两大注意事项
实例题目
超超超详细图解
答案以及详尽总结
后记
题记
复习到离散数学图论时,想起来这个算法,感觉很有写博客的必要!今天这篇博客就来讲一下查找最短路径的Dijkstra算法。
Dijkstra 算法,是由荷兰计算机科学家 Edsger Wybe Dijkstra 在1956年发现的算法,戴克斯特拉算法使用类似广度优先搜索的方法解决赋权图的单源最短路径问题。Dijkstra 算法原始版本仅适用于找到两个顶点之间的最短路径,后来更常见的变体固定了一个顶点作为源结点然后找到该顶点到图中所有其它结点的最短路径,产生一个最短路径树。本算法每次取出未访问结点中距离最小的,用该结点更新其他结点的距离。需要注意的是绝大多数的Dijkstra 算法不能有效处理带有负权边的图。
两大注意事项
需要注意两个问题
1.每次从未标记的节点中选择距离出发点最近的节点,标记它,收录到最短路径集合中。
2.计算刚加入的节点A的临近节点B的距离(不包含标记的节点),若(节点A的距离+节点B的距离到节点B的边长)<节点B,就更新节点B的距离和其前一个位置的点。
实例题目
如图,计算从起点0到终点4的最短路径长度。

超超超详细图解
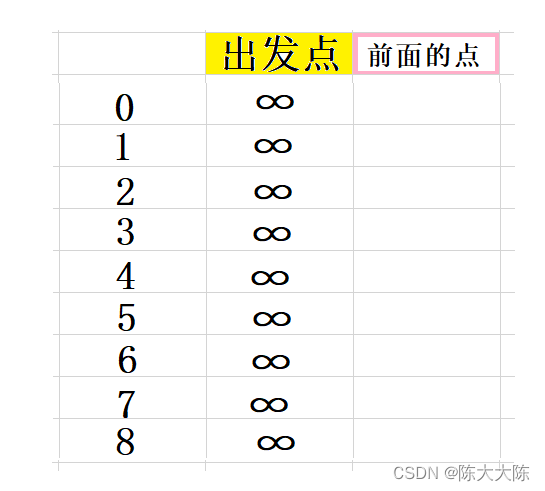
我们作出这样的表格,用于施展Dijkstra算法。
出发点表示从出发点到现在位置地距离。
首先从距离出发点最近的点,也就是出发点开始,它距离出发点的位置显然是0,。
标记它,并收录到最优路径集合中,我们用一个对钩来表示已被收录。

下一步就是找它的临近节点,分别是1和7。
更新1和7的出发点距离和前面点,如图。

紧接着从没有被标记的节点中选出出发点距离最短的,即为1,标记它,并收录到最短路径集合中。
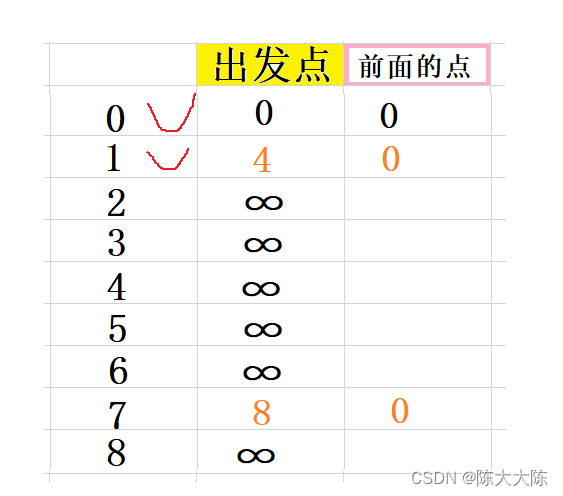
紧接着计算它的邻接节点,即为7和2,因为0已经被标记所以不算。
计算出0和它们的距离分别是15和12,12小于默认的正无穷,更新。
15比8大,不更新。

选出出发点距离最小的点,即为7,标记它,并收录到最短路径集合中。
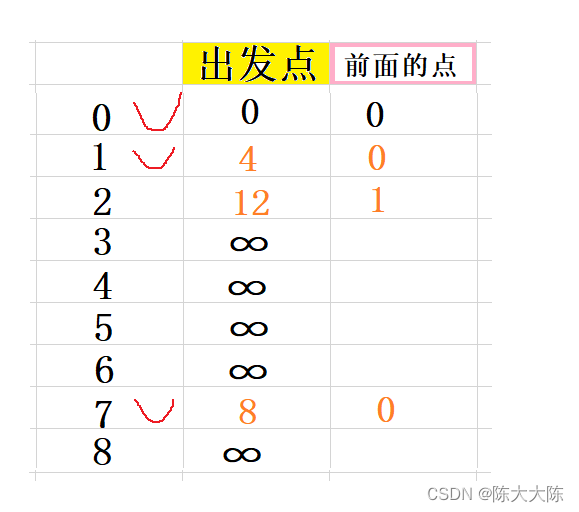
紧接着计算它的邻接节点,即为6和8,因为1和0已经被标记所以不算。
计算出0和它们的距离分别是9和15,小于默认的正无穷,更新。

选出出发点距离最小的点,即为6,标记它,并收录到最短路径集合中。
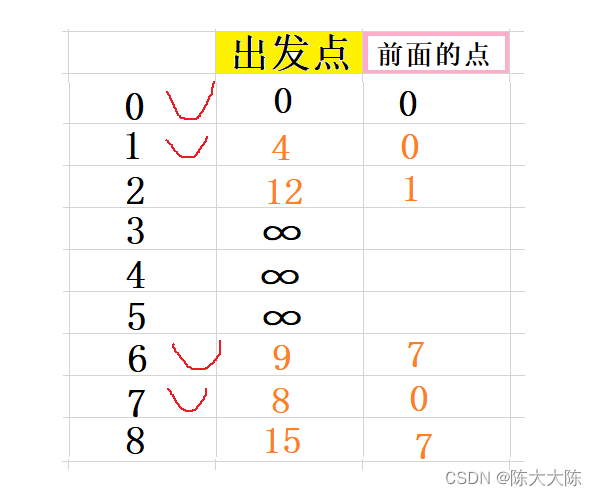
紧接着计算它的邻接节点,即为5和8,因为7已经被标记所以不算。
计算出0和它们的距离分别是11和15,11的更新,15的和之前相等,不更新。

选出出发点距离最小的点,即为5,标记它,并收录到最短路径集合中。

紧接着计算它的邻接节点,即为2,3和4,因为6已经被标记所以不算。
计算出0和它们的距离分别是15和25和21。
15大于12,不更新,25小于正无穷,更新,21小于正无穷,更新。
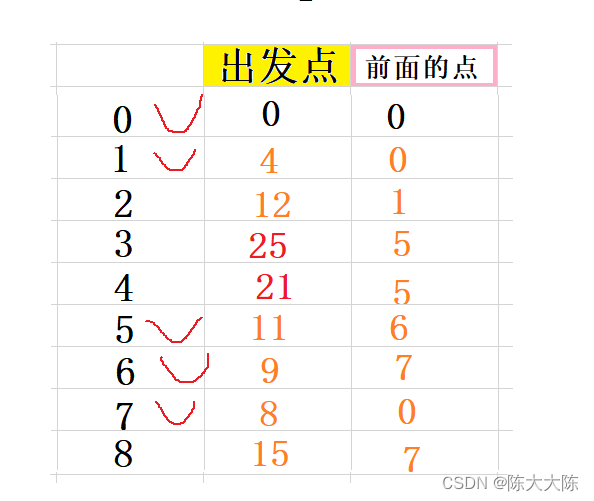
选出出发点距离最小的点,即为2,标记它,并收录到最短路径集合中。

紧接着计算它的邻接节点,即为3和8,因为1和5已经被标记所以不算。
计算出0和它们的距离分别是19和14,分别小于25和15,都更新。
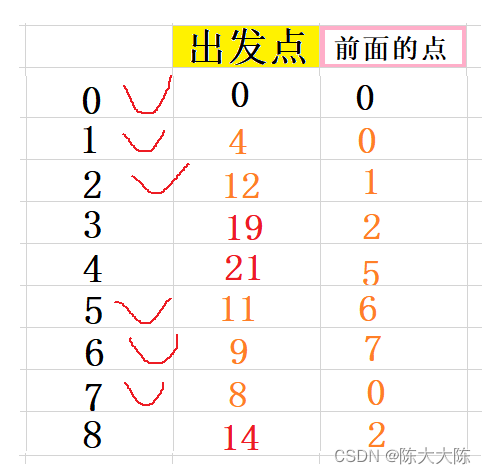
选出出发点距离最小的点,即为8,标记它,并收录到最短路径集合中。

紧接着计算它的邻接节点,全都标记过了,最方便的一集,小时候写哭了。
直接标记后跳过。
选出出发点距离最小的点,即为8,标记它,并收录到最短路径集合中。

紧接着计算它的邻接节点,就剩下一个4没被标记了。
计算出距离它的距离是28,大于21,不更新。
最后一步将4标记,并收录到最短路径集合中。、
我们的最终答案堂堂出炉!!!

答案以及详尽总结
从上面的表中可以得到答案,0到4的最短路径是21。
从头到尾经过的节点是 0 7 6 5 4。
其实需要注意的就这两点。
1.每次从未标记的节点中选择距离出发点最近的节点,标记它,收录到最短路径集合中。
2.计算刚加入的节点A的临近节点B的距离(不包含标记的节点),若(节点A的距离+节点B的距离到节点B的边长)<节点B,就更新节点B的距离和其前一个位置的点。
后记
韩信带净化,成为大牛道阻且长,小僧还在山腰上。。。
博客里如果有问题的话,还请大佬私信我,我会修改的。
有问题的话请私信问我,我看到就会回的。