"A goal is a dream with a deadline." - Napoleon Hill

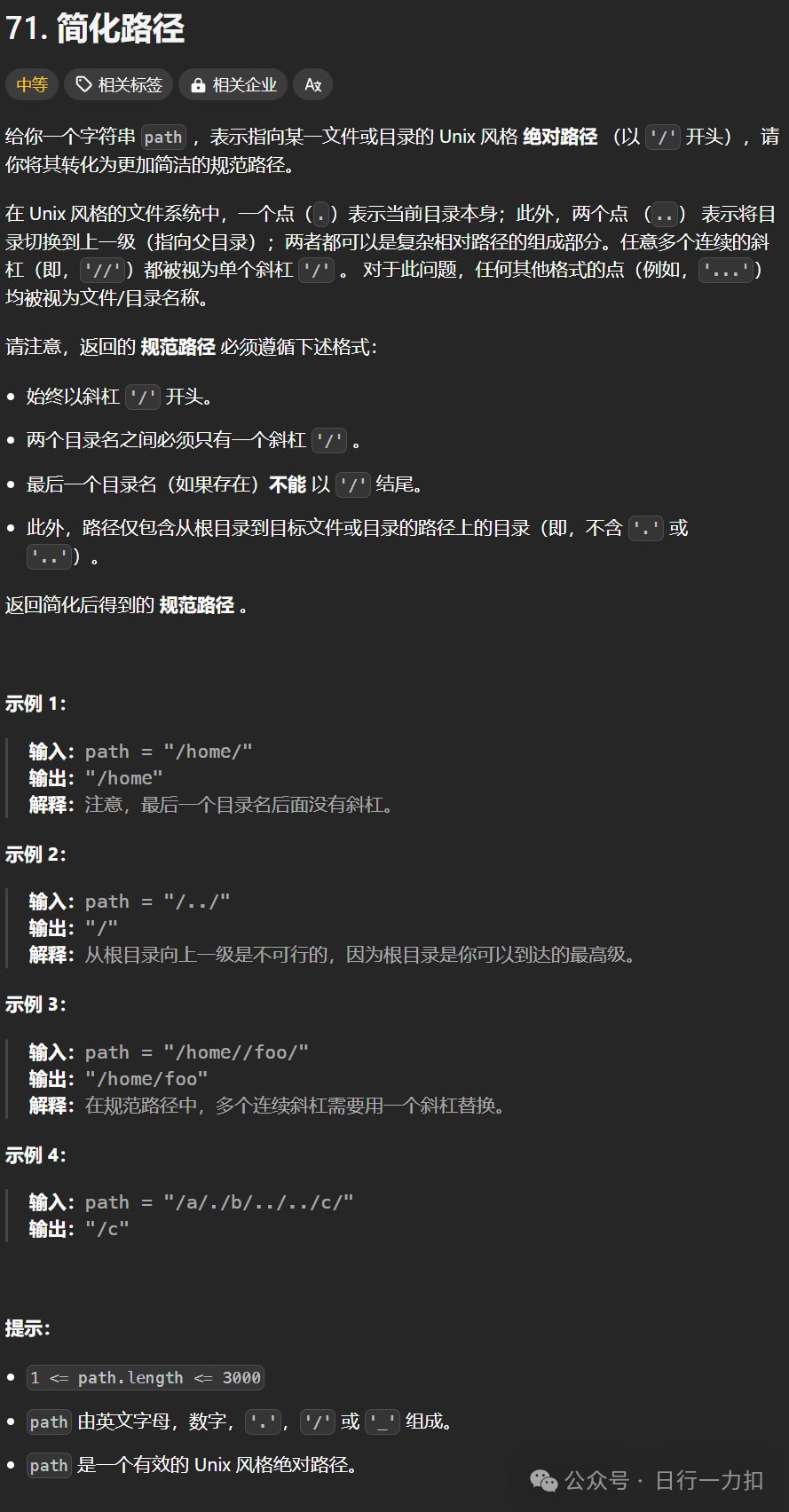
1. 题目描述

2.  题目分析与解析

2.1 思路一

这个题目开始看起来并不太容易知道该怎么写代码，所以不知道什么思路那就先模拟人的行为，比如对于如下测试用例：

首先 /代表根目录，然后向后走，发现 a/，满足规则，继续向后走，发现 ./，其实就是表示当前路径，那说明可以省略，就删除该部分。

继续向后，发现 b/，满足规则，继续向后走，发现 ../，表示当前路径的上一级目录。根据前面走过的步骤，可以知道当前路径为：/a/b，一次回到上一级目录就是 /a。

继续向后走，发现还有一个 ../，又需要回到上一级目录，也就是 /。

最后发现 c/，说明最终的结果是 /c。

而对于如下测试用例：

我们可以发现对于双 /需要特殊处理。

根据以上描述，我们可以粗略的描述一下代码思路：

1. 定义结果字符串，用一个字符数组最好（方便后续按照块删除）

2. 遍历path

3. 截取下一个 /之前的字符

   • 如果发现截取出的是 .，就删除这一小段

   • 如果发现截取出的是 ..，就删除上一个小块的文件地址，比如对于当前路径为 /asad/qwej，如果发现此时截取了 ..，就删除块 /qwej

   • 如果发现是空（对应 // 的情况），就跳过

   • 如果发现是其它字符串，那就在当前块前面加一个 / 然后直接拼接上。（比如当前为/asad/qwej，此时发现对应字符串为 poi，那么就将 "/" + "poi"，拼接在/asad/qwej后面形成/asad/qwej/poi

3.2 思路二

既然我们要处理的特殊情况就那么几种：

1. 出现 .

2. 出现 ..

3. 多余的

4. 正常出现文件路径

那么我们是不是可以

1. 将1视为什么都不做？

2. 将2视为减少一个路径

3. 将3跳过

4. 将4视为增加一个路径

又因为我们要增加或者减少的哪个路径总是在我们刚刚遍历过的地方，也就是之前的路径我不需要管，相当于先进，后来的内容我要进行判断，相当于后出，那么是不是就可以使用栈来解决？（其实思路和思路一没什么区别，就是把数组换成栈了）

所以根据以上内容我们可以写出如下代码思路：

1. 定义一个栈

2. 遍历path

3. 发现出现 .，对栈保持不动

4. 发现出现 ..，就弹栈，直到弹出一个 /

5. 如果发现是空（对应 // 的情况），就跳过

6. 如果发现是其它字符串，那就在当前块前面加一个 / 然后入栈

3. 代码实现

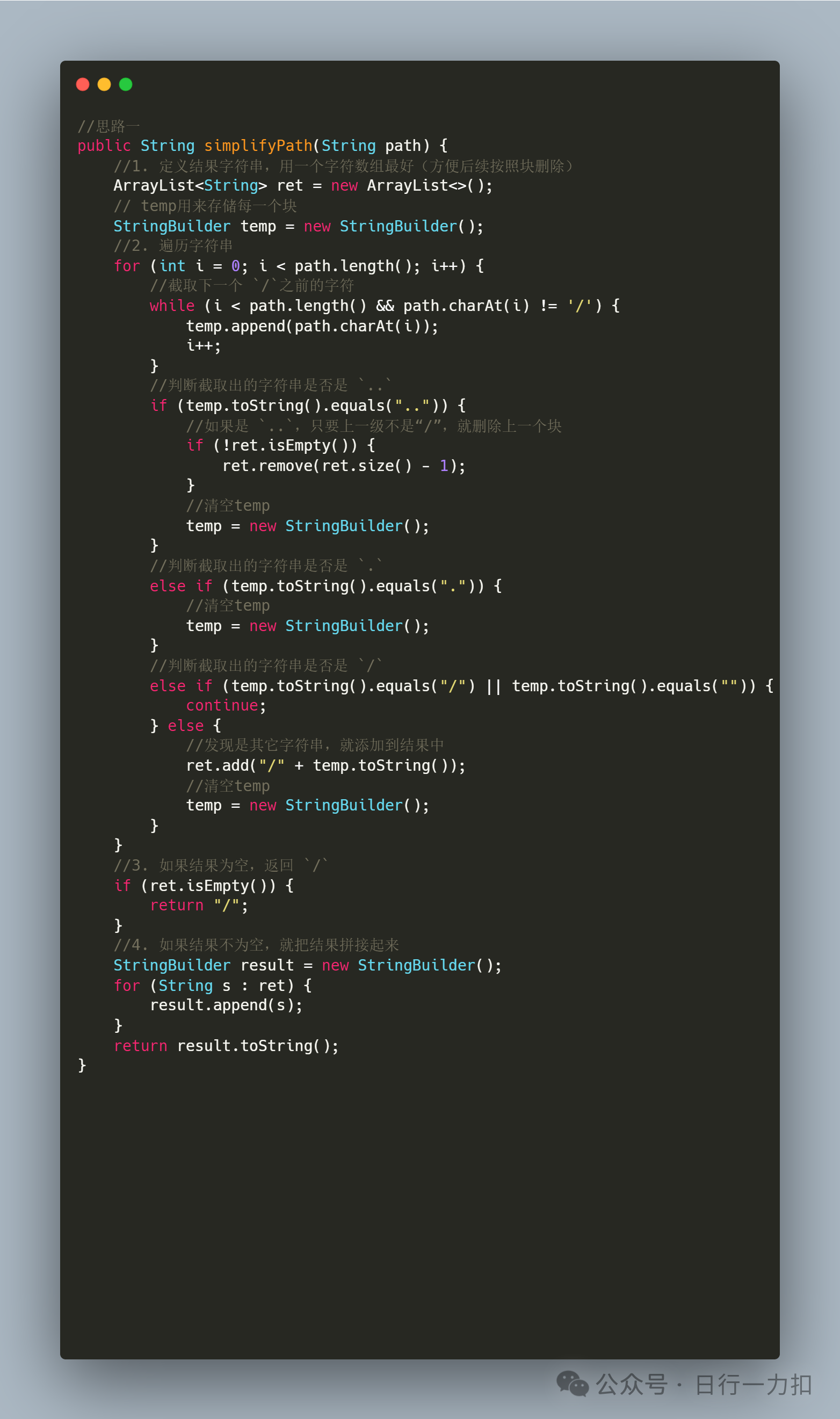
3.1 思路一

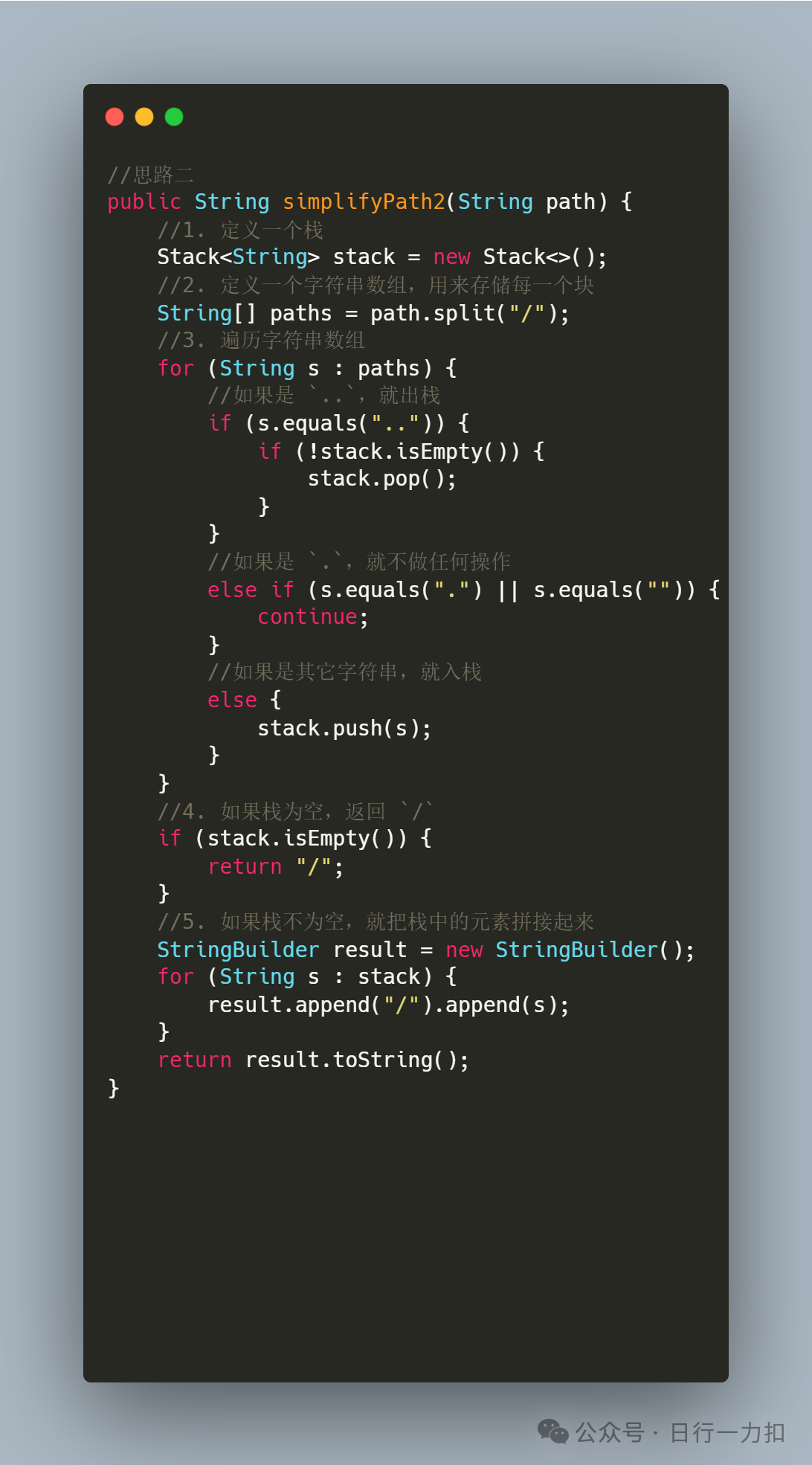
3.2 思路二

4. 相关复杂度分析

思路一：

• 时间复杂度：O(n)，其中 n 是路径字符串的长度。在遍历路径字符串的过程中，执行了一些常数时间的操作，例如字符串拼接、字符串比较等。

• 空间复杂度：O(n)，使用了一个 ArrayList 和一个 StringBuilder。ArrayList 的空间取决于路径中块的数量，而 StringBuilder 的空间取决于路径中每个块的长度。

思路二：

• 时间复杂度：O(n)，其中 n 是路径字符串的长度。首先，通过 split() 方法将路径字符串分割成一个字符串数组，时间复杂度为 O(n)。然后，对字符串数组进行遍历，执行了一些常数时间的操作，例如栈的入栈和出栈操作。

• 空间复杂度：O(n)，使用了一个栈和一个字符串数组。栈的空间取决于路径中块的数量，而字符串数组的空间取决于路径中块的数量以及每个块的平均长度。

综上所述，思路一和思路二的时间复杂度都是线性的，但在空间复杂度上稍有不同。思路一的空间复杂度主要取决于路径中每个块的长度，而思路二的空间复杂度主要取决于路径中块的数量。通常情况下，思路二的空间复杂度略低于思路一。