文章目录
- 推荐系统介绍
- 什么是推荐系统?
- 推荐系统的应用
- 为什么需要推荐系统
- 推荐系统发展
- 推荐系统的目标
- 怎样评价推荐系统效果
- 推荐系统里的常用词
- 推荐系统经典流程
- 推荐系统的难点与挑战
- 涉及技术点分析
- 为什么需要深度学习
- 协同过滤与矩阵分解
- 矩阵分解中的显式与隐式特征
- 基于用户的协同过滤
- 基于物品的协同过滤
- 小例子
- 为什么需要矩阵分解
- 矩阵分解
- 矩阵分解实例
- 隐向量
- 目标函数
- 后续的改进
- 隐式情况分析
- Embedding的作用
推荐系统介绍
什么是推荐系统?
一句话概括,推荐给你感兴趣的视频,商品等,让你入迷。
推荐系统的应用
个性化推荐,优化用户体验,海量数据中快速定位,精准营销。抖音,京东,小红书等这些例子大多数人都耳闻能详。举几个例子
- 抖音:推荐给你喜欢的视频,你就会挪不开眼睛,一看半天就下去了,这样抖音就赚到了流量,在当前这个社会,流量就是钱。
- 京东:当你买了一个键盘后,肯定需要鼠标,鼠标垫啥的,推荐给你,你买的概率会很大,京东也就多挣一份钱呗。
为什么需要推荐系统
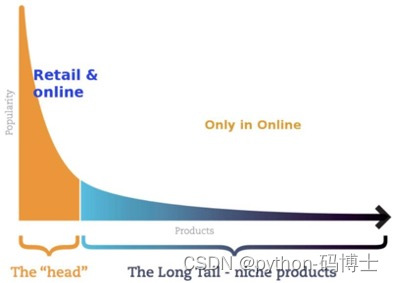
- 卖的好的就那几种商品,其他的不要了?
- 80%的销售来自20%的热门商品
- 要想提高整体收益,得把长尾商品(也就是剩下的80%商品)推出去
- 通过用户行为来进行个性化推荐
推荐系统发展
- 亚马逊1998年就开始用了,只不过那时候还是简单的协同过滤。
- 2006年Netflix(在线视频)竞赛一炮走红
- 2015年开始深度学习崛起,推荐也随之改变
- 今天已经百花齐放,各大论文层出不穷
推荐系统的目标
- Relevance:推荐的东西起码得相关才行
- Novelty:新颖的才好,推的得是人家没有的
- Serendipity:跟处对象一样一样的,机缘
- Diversity:多样性,换着花样玩才好

怎样评价推荐系统效果
- 其实最主要的还是用户满意度,各种数学公式只是辅助判断
- 常规的计算损失: R M S E = 1 ∣ τ ∣ ∑ ( u , i ) ∈ τ ( r ^ u i − r u i ) 2 RMSE =\sqrt{\frac{1}{\left|\tau\right|}\sum\limits_{(u,i)\in\tau}(\hat{r}_{ui}-r_{ui})^2} RMSE=∣τ∣1(u,i)∈τ∑(r^ui−rui)2(T是测试集)
- TopK推荐: p r e c i s i o n @ K = ∣ R e l u ∩ R e c u ∣ ∣ R e c u ∣ precision@K = {\left|Rel_u \cap Rec_u\right| \over \left|Rec_u\right|} precision@K=∣Recu∣∣Relu∩Recu∣(用户相关商品集与推荐商品集的交集)
- 覆盖率:挖掘长尾;多样性:覆盖不同领域;实时性:刚买了房子赶紧推装修
推荐系统里的常用词
- Item:商品,例如要从拼多多买的9.9包邮的拖鞋
- Embedding:隐向量,例如对用户商品评分矩阵进行分解
- 召回:粗略计算要返回结果,例如先从100W商品中取比较可能的100个
- 打分:要排名得有一个统一的标准;重排:最终结果排序
推荐系统经典流程
1、离线+近线+在线(召回+粗排+精排)
2、离线通常跑较大的模型与算法,先得到当前数据的大致结果,一定时间更新一次
3、粗排通常会跟着用户走,用户做了什么事,推荐结果也会随之更新
4、在线模块需要根据业务规则来返回最终呈现结果
推荐系统的难点与挑战
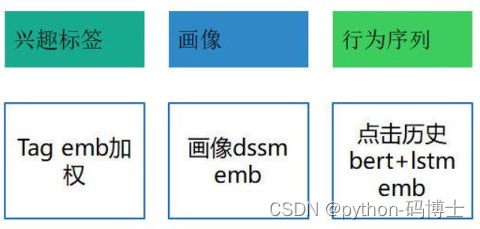
- 需要更广泛的收集用户标签并画像
- 人是善变的,随着时间的推移,兴趣也会改变
- 根据固定画像数据,推荐结果可不能固定不变
- 特征工程如何构建一直是一个大难题

- 推荐系统中的冷启动也是一个问题
冷启动指的是来了一个新人或者新物品。对他不是很熟悉。冷启动包括用户冷启动与商品冷启动;新用户来了,不知道他啥样怎么办;商品倒是好办,属性相对固定,解决方法比较多,例如直接推荐销冠
涉及技术点分析
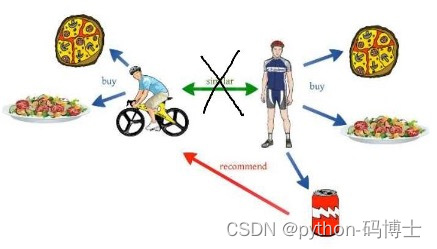
- Embedding方向:如何更好的表示数据,肯定不用one-hot
- 隐向量的方法在推荐中几乎无处不用,例如常见的FM及其DeepFM算法
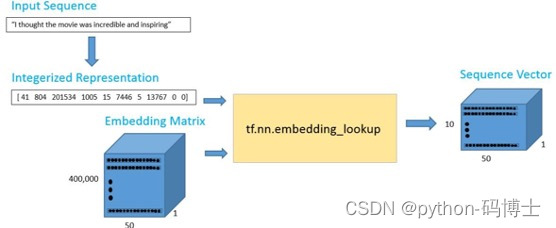
- NLP方向:如何基于文本数据来进行推荐?
- 文本处理方法比较多,LDA,词向量,矩阵分解等套路都能用得上
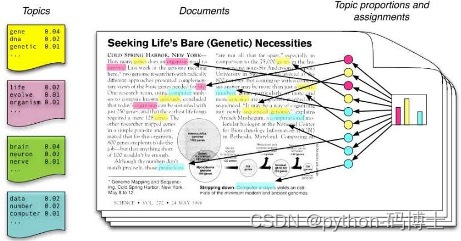
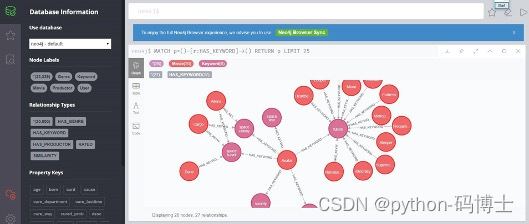
- 知识图谱方向:现在这么火的技术点,推荐中肯定也用到了
- 数据越多,越能体现出知识图谱的强大
- CV方向:卷积与图卷积,图像与视频数据也是用户行为中的体现
- 卷积不仅仅能应用在图像/视频数据中,矩阵数据都可以尝试
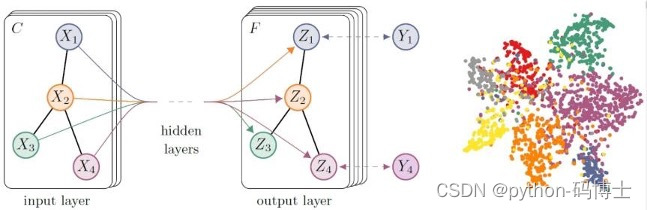
- 特征工程与深度学习方向:如何更好的利用这么多信息?深度学习天生优胜!
- 数据维度大,稀疏度高一直都是一个大难题,与深度学习结合能更简单
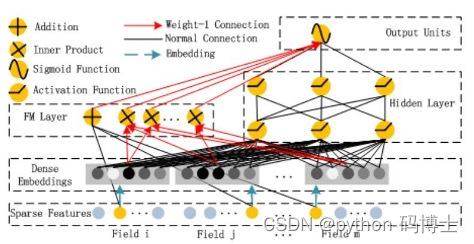
为什么需要深度学习
- 宏观:传统人工特征工程难度较大,深度学习可以把特征做的更好
- 本质:end2end的架构让模型训练起来更容易,项目做起来更简单!
- 深度学习更适合NLP与图像数据,符合当下用户行为数据
- 但凡看到深度学习,第一感觉应该是这件事做起来没那么麻烦了
协同过滤与矩阵分解
矩阵分解中的显式与隐式特征
显式特征:可以直观看到的数据
隐式特征:通过某些操作行为产生的数据
| 用户行为 | 类型 | 特征 | 作用 |
|---|---|---|---|
| 评分 | 显式 | 整数量化的偏好,可能的取值是 [0,n];一般取值为 5 或者是 10 | 通过用户对物品的评分,可以精确的得到用户的偏好 |
| 投票 | 显式 | 布尔量化的偏好,取值是 0 或 1 | 通过用户对物品的投票,可以较精确的得到用户的偏好 |
| 转发 | 显式 | 布尔量化的偏好,取值是 0 或 1 | 而过用户对物品的投票,可以精确的得到用户的偏好 |
| 保存书签 | 显示 | 布尔量化的偏好,取值是 0 或 1 | 通过用户对物品的投票,可以精确的得到用户的偏好 |
| 标记标签 | 显示 | 一些单词,需要对单词进行分析,得到偏好 | 通过分析用户的标签,可以得到用户对项目的理解,同时可以分析出用户的情感: 喜欢还是讨厌 |
| 评论 | 显示 | 一段文字,需要进行文本分析,得到偏好 | 通过分析用户的评论,可以得到用户的情感:喜欢还是讨厌 |
| 点击流 | 隐式 | 一组用户的点击,用户对物品感兴趣,需要进行组分析,得到偏好 | 用户的点击一定程度上反映了用户的注意力,所以它也可以从一定程度上反映用户的喜好. |
| 页面停留时间 | 隐式 | 一组时间信息,噪音大,需要进行去噪分析,得到偏好 | 用户的页面停留时间一定程度上反映了用户的注意力和喜好,但噪音偏大,不好利用。 |
| 购买 | 隐式 | 布尔量化的偏好,取值是 0 或 1 | 用户的购买是很明确的说明这个项目它感兴趣。 |
基于用户的协同过滤
- 首先找到相似用户(相似度计算)
- 属性特征,行为特征等都可以当做计算输入
- User1喜欢1,2,3,4;User3当前喜欢2,3
- 如果这俩用户计算后相似度较高,就可以把1,4推给User3
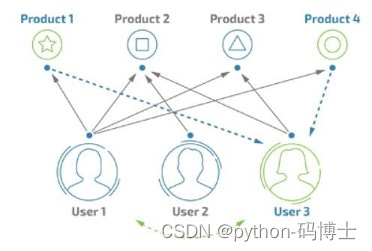
存在的问题:数据稀疏,计算复杂度,人是善变的,冷启动问题,稀疏(通常商品非常多,用户购买的只是其中极小一部分),计算(计算相似度矩阵是个大活,用户和商品都比较多的时候就难了),冷启动(新用户来了怎么办?)
基于物品的协同过滤
- 还是要先得到用户与商品的交互数据
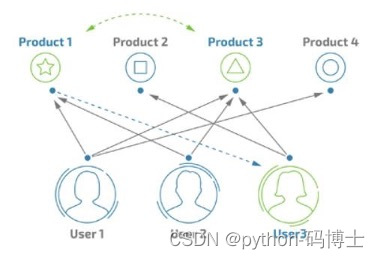
- 此时发现商品1和3经常在一起出现
- 那这俩商品之间肯定有鬼。。。(相关度)
- User3目前只买了商品2和3,此时可以推给他商品1
小例子
首先计算商品之间的相似度(pearson),邻居设置为2,预测r51=?
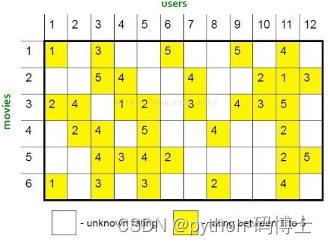
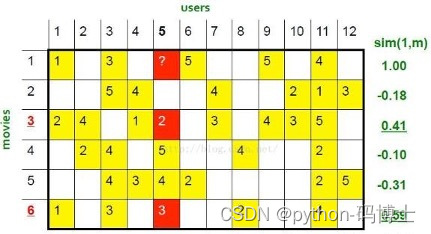
R _ 51 = ( 0.41 ∗ 2 + 0.59 ∗ 3 ) / ( 0.41 + 0.59 ) = 2.6 R\_51 = (0.41*2+0.59*3)/(0.41+0.59)=2.6 R_51=(0.41∗2+0.59∗3)/(0.41+0.59)=2.6
为什么需要矩阵分解
- 用户:1个亿,商品100W,这得是多大的一个矩阵,要命了
- 能不能间接点来求呢?最终目标就是把每个用户对各个商品的喜好预测出来
- 跟找中介租房子差不多,通过中介来重新组合矩阵
- 矩阵分解已经成为推荐系统中用的最多的方法

矩阵分解
- user-item矩阵分解
- 得到user,item两个矩阵
- 原矩阵:m*n(用户,音乐)
- user(mk),item(kn)
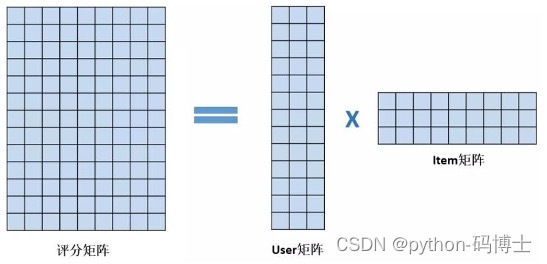
矩阵分解实例
- 用户-歌曲之间的行为数据
- 1代表听过该歌曲,0表示没有
- 可以想象成一个非常稀疏的矩阵
- 目标:预测空白值到底等于多少
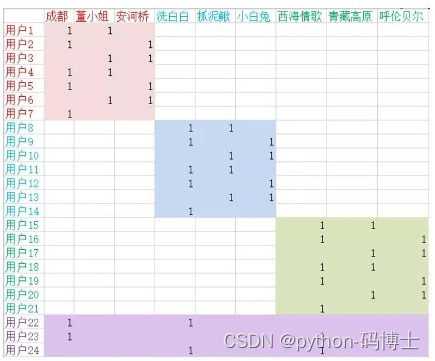

那么存在这么几个问题:
- 这俩矩阵可有实际值
- K等于多少合适呢?
- 其中的数值代表什么?
- 如何计算得到?
目标其实就是得到一个大表,分解后的矩阵还原回这个大表即可,数值即表示对当前商品喜好程度。方法蛮简单,具体怎么做呢?
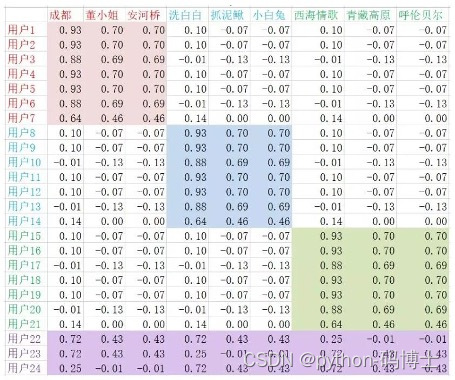
隐向量
其实就是特征的高维表达,只不过很难去理解。例如用户的隐向量可以想象成是这个样子:

用户与商品向量可以当做其特征表示,这可不是随机值,可以观察下数值特点,不同颜色表示特征鲜明的地方,也就是喜好
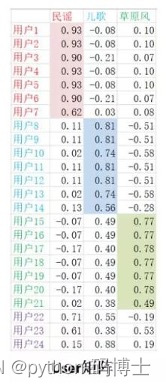
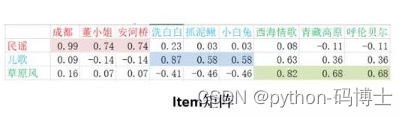
隐向量真的可以理解吗?通常只是比喻而已,一般难以理解,例如一个50维的向量,鬼知道它具体表什么含义,没关系,咱们理解不了无所谓,计算机能更好的理解就可以了
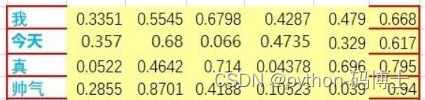
目标函数
- 跟回归方程很像: min X , Y ∑ r u i ≠ 0 ( r u i − x u T y i ) 2 + λ ( ∑ u ) ∣ ∣ x u ∣ ∣ 2 2 + ∑ i ∣ ∣ y i ∣ ∣ 2 2 ) \min\limits_{X,Y}\sum\limits_{r_{ui}\neq0}(r_{ui}-x_u^Ty_i)^2+\lambda(\sum\limits_u)||x_u||_2^2+\sum\limits_i||y_i||_2^2) X,Yminrui=0∑(rui−xuTyi)2+λ(u∑)∣∣xu∣∣22+i∑∣∣yi∣∣22)
- 用户矩阵 X = [ x 1 , x 2 , … … , x N ] X=[x_1,x_2,……,x_N] X=[x1,x2,……,xN]: 商品矩阵: Y = [ y 1 , y 2 , … … , y M ] Y=[y_1,y_2,……,y_M] Y=[y1,y2,……,yM]
- N为用户个数,M为商品个数,还需注意隐向量维度
- 其中还额外引入了正则化惩罚项
后续的改进
- 如果用户就特别刁钻,评分都会很低;如果商品本身就很好,评分都较高
- 这里还需要注意的就是用户与商品的本身属性信息,之前公式中木有涉及
- 在原公式中 min X , Y ∑ r u i ≠ 0 ( r u i − x u T y i ) 2 + λ ( ∑ u ) ∣ ∣ x u ∣ ∣ 2 2 + ∑ i ∣ ∣ y i ∣ ∣ 2 2 ) \min\limits_{X,Y}\sum\limits_{r_{ui}\neq0}(r_{ui}-x_u^Ty_i)^2+\lambda(\sum\limits_u)||x_u||_2^2+\sum\limits_i||y_i||_2^2) X,Yminrui=0∑(rui−xuTyi)2+λ(u∑)∣∣xu∣∣22+i∑∣∣yi∣∣22)分别加入用户与商品偏置项
- 例如bu表示用户偏置,bi表示商品偏置
隐式情况分析
- 用户-商品的评分矩阵做起来非常直接,但是哪有那么正好的事啊
- 通常收集的数据都是用户的行为:观看时间,点击次数等指标
- 这种数据该怎么求解呢?首先定义置信度: c u i = 1 + α r u i c_{ui}=1+\alpha r_{ui} cui=1+αrui
- 置信度默认为1,表示用户没有产生行为的商品;行为越多,置信度越大
- 重新定义评分: p u i = { 0 r u i = 0 1 r u i > 0 p_{ui}= \lbrace_{0\quad r_{ui}=0}^{1\quad r_{ui}>0} pui={0rui=01rui>0 (有行为的则评分为1)
- 新的优化目标: G ( x ∗ , y ∗ ) = ( ∑ u , i c u i ( p u i − x u T y i ) 2 + λ ( ∑ u ∣ ∣ x u ∣ ∣ 2 + ∑ i ∣ ∣ y i ∣ ∣ 2 ) G(x_*,y_*)=({\sum\limits_{u,i}}c_{ui}(p_{ui}-x_u^Ty_i)^2+\lambda(\sum\limits_u||x_u||^2+\sum\limits_i||y_i||^2) G(x∗,y∗)=(u,i∑cui(pui−xuTyi)2+λ(u∑∣∣xu∣∣2+i∑∣∣yi∣∣2)
- 总结起来就是置信度越大的你得预测的越准,要不损失就大了
- 求解过程依旧交替使用最小二乘法,固定Y优化X,再固定X优化Y
Embedding的作用
无处不在的Embedding,Ai的核心其实就是让计算机能更懂我!
NLP,CV领域做得太多啦,推荐中也不例外,Embedding做好啦一切都解决了!