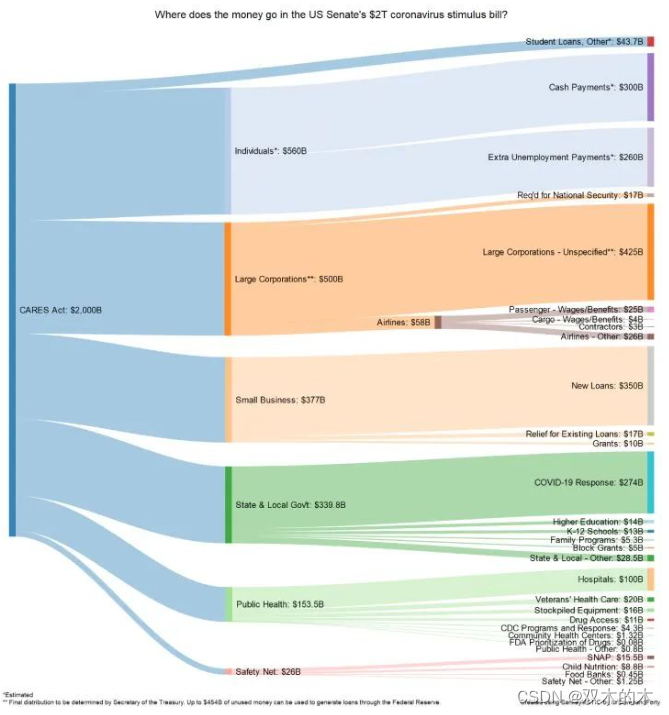
网络世界中时常会遇到这类滑稽的算命小程序，实现原理很简单，随便设计几个问题，根据玩家对每个问题的回答选择一条判断树中的路径（如下图所示），结论就是路径终点对应的那个结点。

现在我们把结论从左到右顺序编号，编号从 $1$ 开始。这里假设回答都是简单的“是”或“否”，又假设回答“是”对应向左的路径，回答“否”对应向右的路径。给定玩家的一系列回答，请你返回其得到的结论的编号。

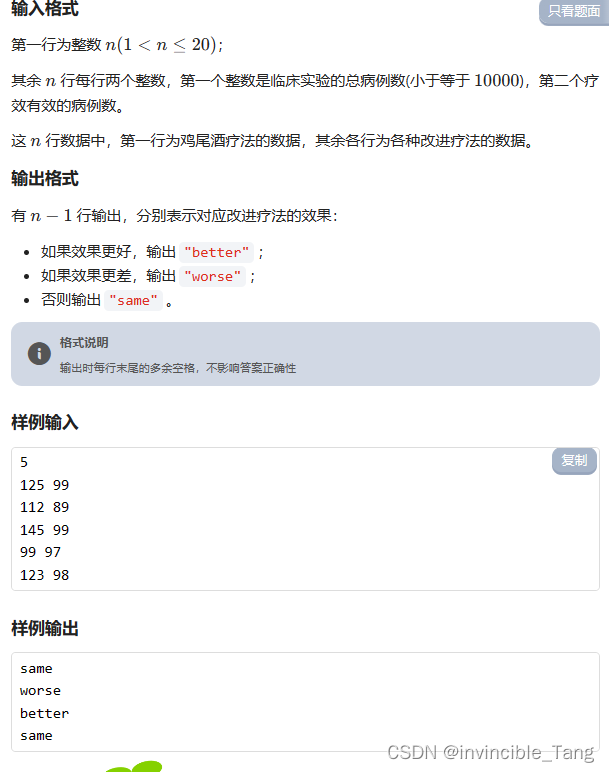
输入格式：
输入第一行给出两个正整数：$N$（≤30）为玩家做一次测试要回答的问题数量；$M$（≤100）为玩家人数。

随后 $M$ 行，每行顺次给出玩家的 $N$ 个回答。这里用 $y$ 代表“是”，用 $n$ 代表“否”。

输出格式：
对每个玩家，在一行中输出其对应的结论的编号。

输入样例：

3 4
yny
nyy
nyn
yyn

输出样例：

3
5
6
2

需要观察得到二叉树的一个规律。
首先定义答案res为1，也就是全为y的时候到达的节点，每次我们遍历由yn组成的字符串的时候，比如在读到第一个字符为n的时候，我们就需要让res加上根节点的叶节点数量，而每次循环到下一个选择点的时候，叶节点都会变为之前的$\frac{1}{2}$，这就是需要找到的规律。

也就是只需要遍历读入的字符串，对于每个字符如果是n，就使答案加上当前的叶节点数量。

#include<iostream>
#include<cmath>
using namespace std;
int main(){int n,m;cin >> n >> m;for(int i = 0;i < m;i++){string str;cin >> str;int res = 1;			//一开始一定是1而不是0int t = pow(2,n);		//计算出根节点的叶节点数量for(int i = 0;i < n;i++){if(str[i] == 'n')res += t/2;t/=2;				//按照规律，每次变为二分之一}cout << res << endl;}return 0;
}