作者简介：大家好，我是未央；

博客首页：未央.303

系列专栏：牛客面试必刷TOP101

每日一句：人的一生，可以有所作为的时机只有一次，那就是现在！！！！！

---

前言

---

一、BM38 在二叉树中找到两个节点的最近公共祖先

题目描述

描述：

给定一棵二叉树(保证非空)以及这棵树上的两个节点对应的val值 o1 和 o2，请找到 o1 和 o2 的最近公共祖先节点。

---

---

举例说明：

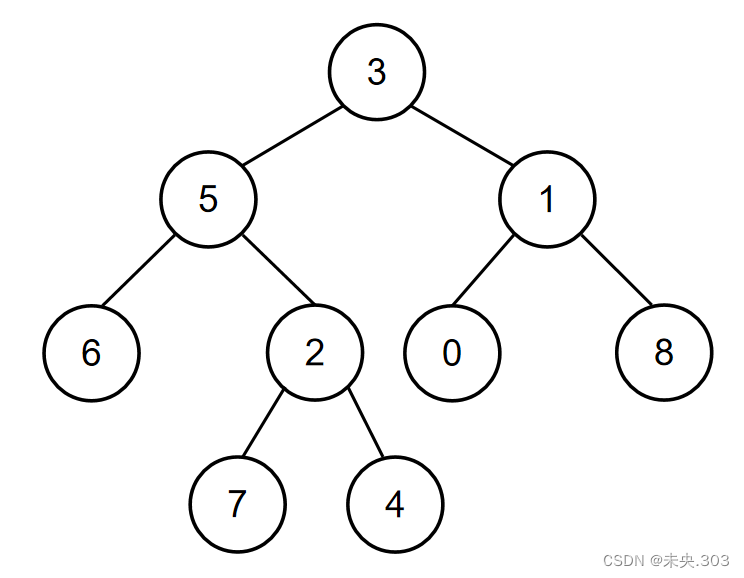
如当输入{3,5,1,6,2,0,8,#,#,7,4},5,1时，二叉树{3,5,1,6,2,0,8,#,#,7,4}如下图所示：

所以节点值为5和节点值为1的节点的最近公共祖先节点的节点值为3，所以对应的输出为3。

节点本身可以视为自己的祖先.

---

示例1:

---

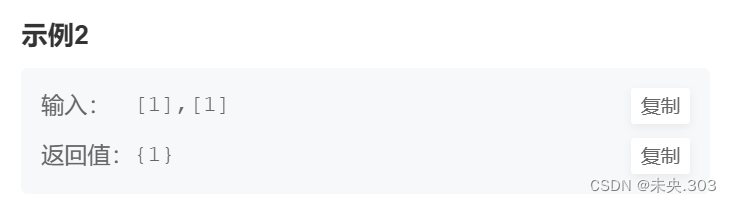
示例2:

---

题目解析

---

---

二、BM40 重建二叉树

题目描述

描述：

给定节点数为 n 的二叉树的前序遍历和中序遍历结果，请重建出该二叉树并返回它的头结点。

---

---

举例说明：

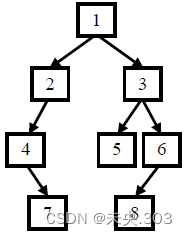
例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建出如下图所示。

---

示例1:

---

示例2:

示例3:

---

题目解析

---

总结