正如模拟滤波器是使用拉普拉斯变换设计的一样,递归数字滤波器也是使用称为z变换的并行技术开发的。这两个变换的总体策略是相同的:用正弦曲线和指数探测脉冲响应,以找到系统的极点和零点。拉普拉斯变换处理微分方程、s 域和 s 平面。相应地,z 变换处理差分方程、z 域和 z 平面。
但是,这两种技术并不是彼此的镜像;s 平面排列在直角坐标系中,而** z 平面使用极坐标格式**。递归数字滤波器通常从经典模拟滤波器之一开始设计,例如巴特沃斯、切比雪夫或椭圆。然后使用一系列数学转换来获得所需的数字滤波器。z 变换为这种数学提供了框架。
1 z 域的本质
为了强调拉普拉斯变换和 z 变换是并行技术,将从拉普拉斯变换开始,并展示如何将其更改为 z-transform。拉普拉斯变换由时域和 s 域信号之间的关系定义:
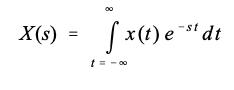
其中 x(t) 和 X(s) 是时域和 s 域表示。该方程根据振幅呈指数变化的正弦波和余弦波来分析时域信号。这可以通过复变量 s 替换成其等价表达式, σ + j ω \sigma+j\omega σ+jω,则公式变成:
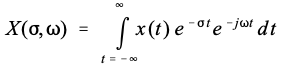
如果只关注实数时域信号(通常的情况),那么 s 平面的上半部分和下半部分是彼此的镜像,并且项简化为简单的余弦波和正弦波。这个等式标识了每个在 s 平面中的位置,即两个参数 σ \sigma σ 和 ω \omega ω。每个位置的值都是一个复数,由一个实部和一个虚部组成。为了找到实部,将时域信号乘以频率为 ω \omega ω 的余弦波,振幅根据衰减参数 σ \sigma σ 呈指数变化。然后, X ( σ , ω ) X(\sigma,\omega) X(σ,ω)的实部的值等于所得波形的积分。虚部的值以类似的方式找到,只是使用正弦波。
拉普拉斯变换可以通过三个步骤转换为 z 变换:
1)第一步是最明显的:从连续信号变为离散信号。这是通过将时间变量 t 替换为样本号 n 并将积分更改为求和来完成的:
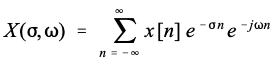
注意,使用括号,表示它是连续的,而不是离散的。尽管现在处理的是离散时域信号 x[n] 。参数 σ , ω \sigma,\omega σ,ω仍然可以采用连续的值范围。
2)第二步是重写指数项。指数信号可以通过以下两种方式之一在数学上表示:

如图 33-1 所示,这两个方程都生成了一条指数曲线。第一个表达式通过参数 σ \sigma σ 控制信号的衰减。如果为正,则随着样本数 n 变形值将减小。同样,如果为负数,曲线将逐渐增加。如果正好为零,则信号的常数值为 1。
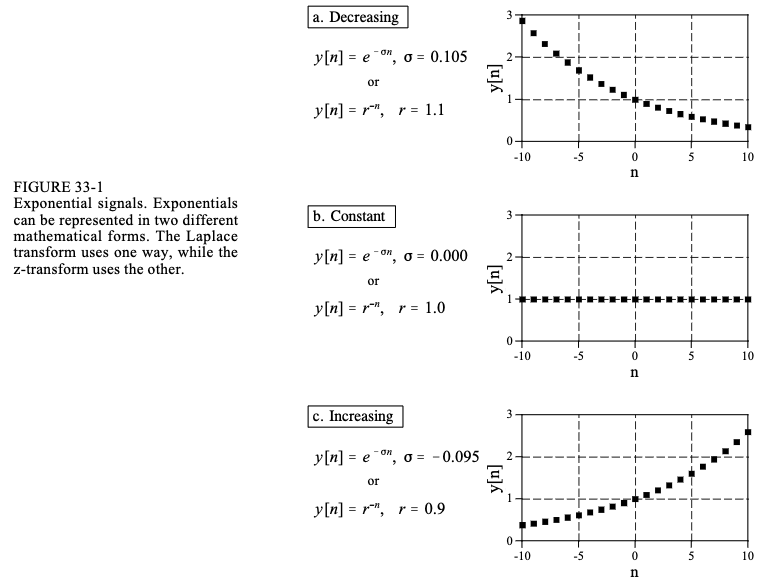
第二个表达式使用参数 r 来控制波形的衰减。如果 r>1 ,则波形将减小,如果 r<1,波形将增加。当 r=1 时,信号将有一个常数值。这两个方程只是表达同一事物的不同方式。可以使用以下关系将一种方法交换为另一种方法:

将拉普拉斯变换转换为 z 变换的第二步是使用其他指数形式完成的:

虽然这是 z 变换的完全正确的表达式,但对于复杂符号来说,它不是最紧凑的形式。这个问题在拉普拉斯变换中通过引入一个新的复变量 s被克服了,其定义为: s = σ + j ω s=\sigma+j\omega s=σ+jω。以同样的方式,将为 z-transform 定义一个新变量:

这是将复变量 z 定义为两个实变量 r 和 ω \omega ω 的极坐标符号组合。
3)推导 z 变换的第三步是将 r 和 ω \omega ω 替换为 z。这将产生 z-transform 的标准形式:

为什么 z 变换使用 r n r^n rn 而不是 e − σ n e^{-\sigma n} e−σn,以及 z 而不是 s?递归滤波器由一组递归系数实现。为了在 z 域中分析这些系统,必须能够将这些递归系数转换为 z 域传递函数,然后再转换回来。
图 33-2 说明了拉普拉斯变换的 s 平面和 z 变换的 z 平面之间的差异。s 平面中的位置由两个参数标识: σ \sigma σ(沿水平轴的指数衰减变量)和 ω \omega ω(沿纵轴的频率变量)。换句话说,这两个实数参数排列在一个直角坐标系中。这种几何结构是通过以下关系定义 s 而产生的,s 是表示平面中位置的复变量,其关系如下: s = σ + j ω s=\sigma+j\omega s=σ+jω 。

相比之下,z 域使用变量:r 和 ω \omega ω,按极坐标排列。与原点的距离 r 是指数衰减的值。从正水平轴测量的角距离 ω \omega ω 就是频率。此几何形状的结果是将 z 定义为: z = r e − j ω z=re^{-j\omega} z=re−jω 。在其他方面,表示 z 平面中位置的复变量是通过将两个实参数以极性形式组合而成的。
这些差异导致 s 平面中的垂直线与 z 平面中的圆相匹配。例如,图 33-2 中的 s 平面显示了极点-零点模式,其中所有极点和零点都位于垂直线上。z平面中的等效极点和零点位于与原点同心的圆上。这可以通过检查前面介绍的关系来理解: σ = − ln ( r ) \sigma=-\ln(r) σ=−ln(r)。
实例中,s 平面的垂直轴(即 σ = 0 \sigma=0 σ=0)对应于 z 平面的单位圆(即 r=1 )。s 平面左半部分的垂直线对应于 z 平面的单位圆内的圆。同样,s 平面右半部分的垂直线与 z 平面单位圆外侧的圆相匹配。换句话说,s平面的左右两侧分别对应于单位圆的内部和外部。例如,当极点占据 s 平面的右半部分时,连续系统是不稳定的。同样,当极点在 z 平面的单位圆之外时,离散系统是不稳定的。当时域信号完全真实时(最常见的情况),z 平面的上半部分和下半部分是彼此的镜像,就像时域一样。
请特别注意频率变量 ω \omega ω 在两个变换中的使用方式。连续正弦波可以具有介于 DC 和无穷大之间的任何频率。这意味着 s 平面必须允许从负无穷大到正无穷大。相比之下,离散正弦波的频率只能介于 DC 和采样率的一半之间。也就是说,当表示为采样率的分数时,频率必须介于 0 和 0.5 之间,当表示为固有频率时,频率必须介于 0 和 π \pi π 之间(即 ω = 2 π f \omega=2\pi f ω=2πf )。这与 z 平面的几何形状相匹配是以弧度表示的角度。也就是说,正频率对应于 0 到 π \pi π 弧度的角度,而负频率对应于 0 到 − π -\pi −π 弧度。由于 z 平面以与 s 平面不同的方式表示频率,因此一些作者使用不同的符号来区分两者。一种常见的表示法是使用 Ω \Omega Ω 表示 z 域中的频率,并使用 ω \omega ω 表示 s 域中的频率。
在 s 平面上,沿垂直轴的值等于系统的频率响应。也就是说,拉普拉斯变换在 σ = 0 \sigma=0 σ=0 处的值等于傅里叶变换。类似地,在 z 域中,频率响应是在单位圆上找到的。这可以通过在z变换(方程33-1)中 r=1 处看到,这导致方程简化为离散时间傅里叶变换(DTFT)。这将零频率(DC)放在s平面水平轴上值为 1 的位置。谱的正频率从该DC位置以逆时针模式排列,占据上半圆。同样,负频率从DC位置沿顺时针路径排列,形成下半圆。谱中的正频率和负频率在 ω = π \omega=\pi ω=π和 ω = − π \omega=-\pi ω=−π 处相遇。这种圆形几何形状也对应于离散信号的频率谱是周期性的。也就是说,当频率角增加到 π \pi π 以上时,会遇到与 0 到 π \pi π 之间相同的值。
2 递归系统分析
递归滤波器由微分方程定义:
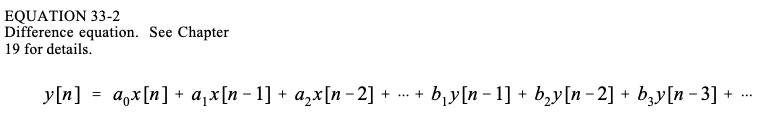
式中x[]、y[]是输入和输出信号。a 和 b 是递归系数。它代表了输入和输出之间的数学关系,必须不断满足。正如连续系统由微分方程控制一样,递归离散系统也按照这个微分方程运行。从这种关系中,可以推导出系统的关键特征:脉冲响应、阶跃响应、频率响应、零极点图等。
通过取方程 33-2 两侧的 z 变换(方程 33-1)开始分析。 想看看这种控制关系在 z 域中是什么样子的。使用相当多的代数,可以将关系分为:Y[z]/X[z] ,即 z 域表示输出信号除以输入信号。就像拉普拉斯变换,这称为系统的传递函数(system’s transfer function),并用 H(z) 来指定。以下是发现:
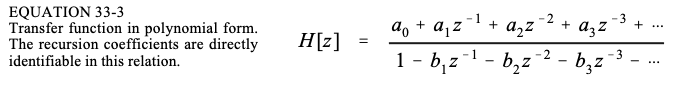
这是编写传递函数的两种方法之一。这种形式很重要,因为它直接包含递归系数。例如,假设知道数字滤波器的递归系数,例如从设计表中提供的递归系数:

直接写下系统的传递函数:

注意,“b”系数进入传递函数时,它们前面有一个负号。 或者,一些作者使用加法来写这个方程,但改变所有“b”系数的符号。这就是问题所在。如果给定一组递归系数(例如来自表格或滤波器设计程序),则“b”系数有 50-50 的几率与预期相反。如果没有发现这种差异,过滤器将非常不稳定。
方程33-3使用 z 的负幂次来表示传递函数,例如: z − 1 , z − 2 , z − 3 z^-1, z^-2, z^-3 z−1,z−2,z−3 等等。当将实际的一组递归系数代入后,可以将传递函数转换为使用正幂次的更传统形式,即: z , z 2 , z 3 z, z^2, z^3 z,z2,z3 。通过将示例的分子和分母都乘以 z 4 z^4 z4,得到:
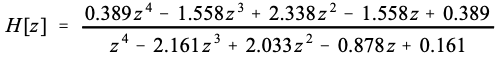
正幂通常更容易使用,并且某些 z-domain 技术需要它们。为什么不直接用正幂重写方程33-3,而完全忘记负幂呢?不能!将分子和分母乘以 z 的最高幂的技巧只能在递归系数数已知的情况下使用。等式 33-3 是针对任意数量的系数编写的。关键是,DSP中经常使用正功率和负功率,需要知道如何在两种形式之间进行转换。
递归系统的传递函数很有用,因为它可以以递归系数无法操作的方式进行操作。这包括以下任务:将级联和并联级组合到一个系统中,通过指定极点和零点位置来设计滤波器,将模拟滤波器转换为数字滤波器等。这些运算由在 z-domain 中执行的代数执行,例如:乘法、加法和因式分解。完成这些运算后,传递函数以方程 33-3 的形式放置,从而可以识别新的递归系数。
与 s 域一样,z 域的一个重要特征是传递函数可以表示为极点和零点。这提供了 z 域的第二种一般形式:

每一个极点(p1, p2, p3等)和零点(z1, z2, z3等)都是一个复数。从方程33-4到33-3的过程中,需要扩展表达式并合并同类项。尽管这涉及大量的代数运算,但原则上很简单,并且很容易编写成计算机程序。然而,从方程33-3到33-4的转换更为困难,因为它需要对多项式进行因式分解。如果传递函数的阶数不超过二阶(即z的幂次不超过 z 2 z^2 z2),则可以使用二次方程进行因式分解。对于高于二阶的系统,通常无法使用代数方法进行因式分解,而必须采用数值方法。
与所有复数一样,极点和零点位置可以用极坐标或矩形形式表示。极坐标表示法的优点是与 z 平面的自然组织更加一致。相比之下,矩形形式通常更适合数学工作,也就是说,它通常更容易操作: σ + j ω \sigma+j\omega σ+jω,与: r e i w re^{iw} reiw相比。
作为使用这些方程的示例,将通过以下步骤设计notch滤波器:
- 1)指定 z 平面中的极点零位置
- 2)以方程 33-4 的形式写下传递函数
- 3)将传递函数重新排列为方程 33-3 的形式
- 4)确定实现滤波器所需的递归系数。
图 33-3 显示了使用的示例:由两个极点和两个零点组成的notch滤波器,位于:


要了解为什么这是一个陷波滤波器,请将此零极点图与图 32-6(s 平面中的notch滤波器)进行比较。唯一的区别是,沿着单位圆移动以找到来自 z 平面的频率响应,而不是沿垂直轴移动以找到来自 s 平面的频率响应。从极点和零点的极性形式可以看出,notch将出现在固有频率 π / 4 \pi/4 π/4 ,对应于 0.125 的采样率。
由于极点和零点位置是已知的,因此传递函数可以以方程 33-4 的形式编写,只需插入以下值:
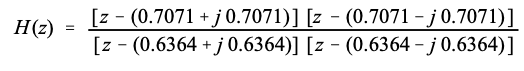
为了找到实现此滤波器的递归系数,必须将传递函数重新排列为方程 33-3 的形式。首先,通过将项相乘来扩展表达式:
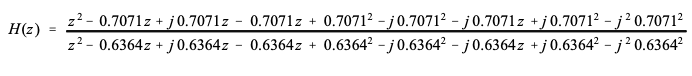
接下来,收集相似的项并减少。只要 z-plane 的上半部分是下半部分的镜像(如果处理的是真正的脉冲响应,情况总是如此),所有包含 j j j 的项将被消除:

虽然这是以一个多项式除以另一个多项式的形式,但它没有像方程 33-3 所要求的那样使用 z 的负指数。这可以通过将分子和分母除以表达式中 z 的最高幂来改变,在本例中为 z 2 z^2 z2:

由于传递函数现在采用方程 33-3 的形式,因此可以通过检查直接提取递归系数:

此示例提供了从极点零图获取递归系数的一般策略。在特定情况下,可以推导更简单的方程,将极点-零点位置与递归系数直接相关。例如,包含两个极点和两个零点的系统(称为双二阶 biquad)具有以下关系:

一旦指定了传递函数,如何找到频率响应呢?有三种方法:一种是数学方法,另外两种是计算(编程)方法。
1)数学方法基于在 z 平面上找到单位圆上的值。这是通过评估传递函数 H(z)(r=1)来完成的。具体来说:
- 首先将 H(z) 转移函数写为等式33-3或33-4的形式。
- 然后,将每个z替换为 e − j w e^{-jw} e−jw(即 r e i w , r = 1 re^{iw},r=1 reiw,r=1)。这为频率响应提供了一个数学方程 H ( ω ) H(\omega) H(ω)。然而,得到的表达式 H ( ω ) H(\omega) H(ω) 非常不方便。通常需要大量的代数运算才能获得可识别的内容,如幅度和相位。虽然这种方法为频率响应提供了精确的方程,但很难在计算机程序中自动化。
2)求频率响应的第二种方法也使用在单位圆上计算 z 平面。不同之处在于,只计算频率响应的样本,而不是整个曲线的数学解。一个计算机程序可能在 ω = 0 \omega=0 ω=0 和 ω = π \omega=\pi ω=π 之间循环 1000 个等距的频率。
这种方法效果很好,经常用于滤波器设计包中。其主要局限性在于,它没有考虑影响系统特性的舍入噪声。即使这种方法发现的频率响应看起来很完美,实现的系统也可能完全不稳定!
3)这就引出了第三种方法:从实际用于实现滤波器的递归系数中找到频率响应。首先,通过将脉冲传递到系统中来找到滤波器的脉冲响应。在第二步中,采用脉冲响应的DFT(当然使用FFT)来求出系统的频率响应。此过程唯一要记住的关键项目是,必须从脉冲响应中获取足够的样本,以便丢弃的样本无关紧要。
3 级联和并联级
复杂的递归滤波器通常分阶段设计,以简化 z 域的繁琐代数。图 33-4 说明了可以安排单个阶段的两种常见方式:级联级和具有附加输出的并行级。例如,低通和高通级可以级联以形成带通滤波器。同样,低通级和高通级的并联组合可以形成带阻滤波器。将这两个阶段称为系统 1 和系统 2 的组合,它们的递归系数分别称为: a 0 , a 1 , a 2 , b 1 , b 2 a_0,a_1,a_2,b_1,b_2 a0,a1,a2,b1,b2 和 A 0 , A 1 , A 2 , B 1 , B 2 A_0,A_1,A_2,B_1,B_2 A0,A1,A2,B1,B2 。目标是将这些阶段(级联或并行)组合成一个递归滤波器,称之为系统 3(system 3),递归系数为: a 0 , a 1 , a 2 , a 3 , a 4 , b 1 , b 2 , b 3 , b 4 a_0,a_1,a_2,a_3,a_4,b_1,b_2,b_3,b_4 a0,a1,a2,a3,a4,b1,b2,b3,b4。

级联中系统的频率响应是通过乘法组合的。此外,并联系统的频率响应通过加法进行组合。z 域传递函数遵循这些相同的规则。这允许通过将问题移动到 z 域,执行所需的乘法或加法,然后返回到最终系统的递归系数来组合递归系统。
作为这种方法的一个例子,将计算出在级联中组合两个双二阶阶段的代数。每个阶段的传递函数通过使用适当的递归系数写出方程 33-3 来求得。然后通过乘以传递来找到整个系统的传递函数 H[z],然后将传递函数的两个阶段相乘找到:

将多项式相乘并收集相似项:

由于这是方程 33-3 的形式,可以直接提取实现级联系统的递归系数:

这种技术的明显问题是需要大量的代数来乘法和重新排列多项式项。幸运的是,整个算法可以用一个简短的计算机程序来表达,如表33-1所示。尽管级联和并行组合需要不同的数学运算,但它们使用几乎相同的程序。特别是,两种算法之间只有一行代码不同,允许将两者组合成一个程序。

该程序的运行方式是将每个阶段的递归系数更改为传递函数,其形式为方程 33-3(第 220270 行)。在以适当的方式组合这些传递函数(第 290-380 行)后,信息将移回递归系数(第 400 行至第 430 行)。
这个程序的核心在于如何表示和组合传递函数的多项式。例如,正在组合的第一阶段的分子是: a 0 + a 1 z − 1 + a 2 z − 2 + a 3 z − 3 a_0+a_1z^{-1}+a_2z^{-2}+a_3z^{-3} a0+a1z−1+a2z−2+a3z−3。 这个多项式在程序中通过存储系数: a 0 , a 1 , a 2 , a 3 , . . . a_0, a_1, a_2, a_3,... a0,a1,a2,a3,... 来表示。同样地,第二阶段的分子由 A 1 [ 0 ] , A 1 [ 1 ] , A 1 [ 2 ] , A 1 [ 3 ] . . . A1[0], A1[1], A1[2], A1[3]... A1[0],A1[1],A1[2],A1[3]... 表示,这些值存储在数组中,而组合系统的分子由 A 3 [ 0 ] , A 3 [ 1 ] , A 3 [ 2 ] , A 3 [ 3 ] . . . A3[0], A3[1], A3[2], A3[3]... A3[0],A3[1],A3[2],A3[3]... 表示。这个程序的目的是只通过引用多项式的系数来表示和操作多项式。
问题是,已知 A1[] 和 A2[],如何计算 A3[]?答案是,当两个多项式相乘时,它们的系数是通过卷积得到的。用数学方程表示就是:A1[]*A2[]=A3[]. 这允许使用标准的卷积算法来找到级联阶段的传递函数,通过对两个分子数组和两个分母数组进行卷积来实现。
组合并行阶段的过程稍微复杂一些。在代数中,分数是根据以下公式相加的:
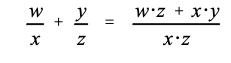
由于每个传递函数都是分数(一个多项式除以另一个多项式),通过将分母相乘并在分子中添加叉积来并行组合阶段。这意味着分母的计算方式与级联阶段的计算方式相同,但分子计算更为复杂。在第 340 行中,对级联阶段的分子进行卷积以找到组合传递函数的分子。在第 350 行中,平行阶段组合的分子计算为两个分子与两个分母的卷积之和。第 360 行处理这两种情况的分母计算。
4 光谱反演
如图33-5所示,频谱反转是通过从原始信号中减去系统的输出来实现的。此过程可以被视为并行组合两个阶段,其中一个阶段恰好是恒定系统(identity system,输出与输入相同)。使用这种方法,可以证明“b”系数保持不变,修改后的“a”系数由下式给出:

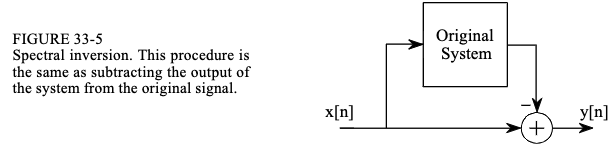
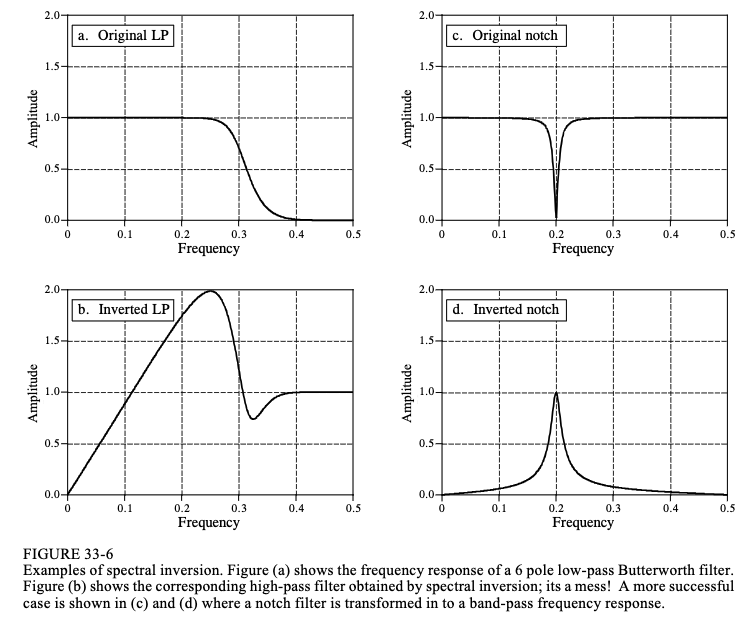
图33-6显示了两种常见频率响应的频谱反转:低通滤波器(a)和notch滤波器(c)。这分别产生一个高通滤波器(b)和一个带通滤波器(d)。
5 增益变化
假设有一个递归滤波器,需要修改递归系数,使输出信号的幅度发生变化。例如,可能需要这样做,以确保滤波器在通带中具有单位增益。实现这一点的方法非常简单:将“a”系数乘以希望增益变化的任何系数,而不理会“b”系数。
在调整增益之前,可能想知道它的当前值。由于增益必须在通带中的某个频率下指定,因此该过程取决于所使用的滤波器类型。低通滤波器的增益测量频率为零,而高通滤波器使用允许的最大频率 0.5。推导这两个特殊频率下增益的表达式非常简单。这是如何完成的。
首先,推导一个零频率增益的方程。这个想法是强制每个输入样本的值为 1,导致每个输出样本的值为 G,即试图找到的系统的增益。从编写递归方程开始,即输入和输出信号之间的数学关系:

接下来,为每个输入样本插入一个1,为每个输出样本插入 G。换句话说,强制系统以零频率运行。等式变为:
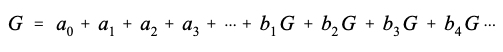
求解 G 时,根据系统的递归系数,提供系统在零频率下的增益:

要使滤波器在直流时具有 1 的增益,请使用此关系式计算现有增益,然后将所有“a”系数除以 G。
0.5 频率下的增益以类似的方式找到:强制输入和输出信号以该频率工作,并观察系统如何响应。当频率为 0.5 时,输入信号中的样本在 -1 和 1 之间交替,即连续样本为:1、-1、1、-1、1、-1、1等。相应的输出信号也以符号交替出现,幅度等于系统的增益:G、-G、G、-G、G、-G 等。将这些信号代入递归方程:

求解 G 时,系统增益频率为 0.5,使用其递归系数:
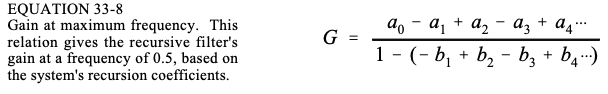
和以前一样,可以通过将所有“a”系数除以 G 的计算值来归一化滤波器以获得单位增益。 在计算机程序中计算方程 33-8 需要一种方法来生成奇数系数的负号和偶数系数的正号。最常见的方法是将每个系数乘以 ( − 1 ) k (-1)^k (−1)k,其中 k 是系数索引。即当 k 遍历以下值:0、1、2、3、4、5、6 等时,表达式取值:1,-1、1、-1、1、-1、1 等。