机器学习流程—数据预处理下篇
我们在机器学习项目开发过程中遇到的大多数现实数据集都具有混合数据类型的列。这些数据集由分类列和数字列组成。然而,各种机器学习模型不适用于分类数据,为了使这些数据适合机器学习模型,需要将其转换为数值数据。例如,假设数据集有一个Gender列,其中包含Male 和 Female等分类元素。这些标签没有特定的偏好顺序,而且由于数据是字符串标签,机器学习模型会误解其中存在某种层次结构。
解决此问题的一种方法是标签编码,我们将为这些标签分配一个数值,例如将Male和Female映射到0和1。但这可能会在我们的模型中增加偏差,因为它将开始对女性参数给予更高的偏好,即 1>0,但理想情况下,两个标签在数据集中同样重要。为了解决这个问题,我们将使用 One Hot Encoding 技术。
One Hot Encoding
优点
它允许在需要数字输入的模型中使用分类变量。
它可以通过向模型提供有关分类变量的更多信息来提高模型性能。
它可以帮助避免序数问题,当分类变量具有自然排序(例如“小”、“中”、“大”)时可能会出现序数问题。
缺点
它可能会导致维度增加,因为为变量中的每个类别创建一个单独的列。这会使模型变得更加复杂并且训练速度变慢。
它可能会导致数据稀疏,因为大多数观测值在大多数 one-hot 编码列中的值为 0。
它可能会导致过度拟合,特别是当变量中有很多类别且样本量相对较小时。
One Hot Encoding 是一种处理分类数据的强大技术,但它可能导致维度增加、稀疏性和过度拟合。谨慎使用它并考虑其他方法(例如序数编码或二进制编码)非常重要。
示例
在One Hot Encoding中,分类参数将男性和女性标签分别设置成单独的列。因此,只要有男性,男性列中的值为 1,女性列中的值为 0,反之亦然。让我们通过一个例子来理解:考虑给出水果及其相应的分类值和价格的数据。
| 水果 | 水果的分类价值 | 价格 |
|---|---|---|
| 苹果 | 1 | 5 |
| 芒果 | 2 | 10 |
| 苹果 | 1 | 15 |
| 橙子 | 3 | 20 |
对数据应用 one-hot 编码后的输出如下:
| 苹果 | 芒果 | 橙子 | 价格 |
|---|---|---|---|
| 1 | 0 | 0 | 5 |
| 0 | 1 | 0 | 10 |
| 1 | 0 | 0 | 15 |
| 0 | 0 | 1 | 20 |
使用 Python 进行 One-Hot 编码
创建一个数据集以从 CSV 文件实现One-Hot编码。
# Program for demonstration of one hot encoding # import libraries
import numpy as np
import pandas as pd # import the data required
data = pd.read_csv('employee_data.csv')
print(data.head()) 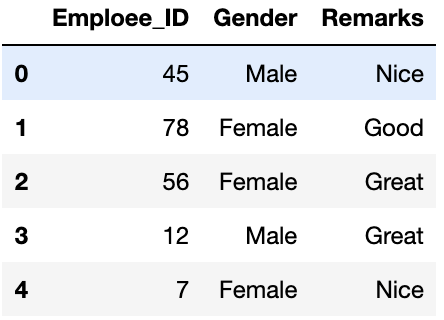
分类列中的唯一值
我们可以使用[pandas库中的unique函数从数据帧的列中获取唯一元素。
print(data['Gender'].unique())
print(data['Remarks'].unique())
输出
array(['Male', 'Female'], dtype=object)
array(['Nice', 'Good', 'Great'], dtype=object)
列中元素的计数
data['Gender'].value_counts()
data['Remarks'].value_counts()
输出
Female 7
Male 5
Name: Gender, dtype: int64Nice 5
Great 4
Good 3
Name: Remarks, dtype: int64
使用pandas
使用pandas 的get_dummies 方法实现
one_hot_encoded_data = pd.get_dummies(data, columns = ['Remarks', 'Gender'])
print(one_hot_encoded_data)

我们可以观察到数据中有3 个“Remarks”列和2 个“Gender”列。
但是,如果有n 个唯一标签,则可以仅使用n-1列来定义参数。例如,如果我们只保留Gender_Female列并删除Gender_Male列,那么我们也可以传达整个信息,当标签为 1 时,表示女性,当标签为 0 时表示男性。这样我们就可以对分类数据进行编码并减少参数的数量。
使用 Sci-kit Learn
Scikit-learn(sklearn) 是 Python 中流行的机器学习库,提供了大量用于数据预处理的工具。它提供了一个OneHotEncoder函数,我们可以在实现该算法之前将分类变量和数值变量编码为二进制向量。确保必须对分类值进行标记和编码,因为 one-hot 编码仅采用数字分类值。
# importing libraries
import pandas as pd
import numpy as np
from sklearn.preprocessing import OneHotEncoder # Retrieving data
data = pd.read_csv('Employee_data.csv') # Converting type of columns to category
data['Gender'] = data['Gender'].astype('category')
data['Remarks'] = data['Remarks'].astype('category') # Assigning numerical values and storing it in another columns
data['Gen_new'] = data['Gender'].cat.codes
data['Rem_new'] = data['Remarks'].cat.codes # Create an instance of One-hot-encoder
enc = OneHotEncoder() # Passing encoded columns enc_data = pd.DataFrame(enc.fit_transform( data[['Gen_new', 'Rem_new']]).toarray()) # Merge with main
New_df = data.join(enc_data) print(New_df) 输出
Employee_Id Gender Remarks Gen_new Rem_new 0 1 2 3 4
0 45 Male Nice 1 2 0.0 1.0 0.0 0.0 1.0
1 78 Female Good 0 0 1.0 0.0 1.0 0.0 0.0
2 56 Female Great 0 1 1.0 0.0 0.0 1.0 0.0
3 12 Male Great 1 1 0.0 1.0 0.0 1.0 0.0
4 7 Female Nice 0 2 1.0 0.0 0.0 0.0 1.0
5 68 Female Great 0 1 1.0 0.0 0.0 1.0 0.0
6 23 Male Good 1 0 0.0 1.0 1.0 0.0 0.0
7 45 Female Nice 0 2 1.0 0.0 0.0 0.0 1.0
8 89 Male Great 1 1 0.0 1.0 0.0 1.0 0.0
9 75 Female Nice 0 2 1.0 0.0 0.0 0.0 1.0
10 47 Female Good 0 0 1.0 0.0 1.0 0.0 0.0
11 62 Male Nice 1 2 0.0 1.0 0.0 0.0 1.0
这里我们将 enc.fit_transform() 方法转换为数组,因为 OneHotEncoder 的 fit_transform 方法返回 SpiPy 稀疏矩阵,因此当我们有大量分类变量时,首先转换为数组可以节省空间。
虚拟变量陷阱
前面我们使用One Hot Encoding 生成的变量就可称之为虚拟变量
在统计学中,特别是在回归模型中,我们处理各种类型的数据。数据可以是定量(数字)或定性(分类)的。数值数据可以在回归模型中轻松处理,但我们不能直接使用分类数据,它需要以某种方式进行转换。
为了将类别属性转换为数值属性,我们可以使用标签编码过程(标签编码为每个数据类别分配一个唯一的整数)。但这个过程并不是唯一合适的,因此,在标签编码之后的回归模型中使用了One Hot Encoding ,这使我们能够根据分类属性中存在的类别数量创建新属性,即如果分类属性中有n个类别,则将创建n 个新属性。创建的这些属性称为虚拟变量。因此,虚拟变量是回归模型中分类数据的“代理”变量。 这些虚拟变量将使用 one-hot编码
创建,每个属性的值为 0 或 1,表示该属性是否存在。
虚拟变量陷阱: 虚拟变量陷阱是一种场景,其中属性高度相关(多重共线性),并且一个变量可以预测其他变量的值。当我们使用one-hot 编码来处理分类数据时,可以借助其他虚拟变量来预测一个虚拟变量(属性)。因此,一个虚拟变量与其他虚拟变量高度相关。在回归模型中使用所有虚拟变量会导致虚拟变量陷阱。因此,回归模型的设计应排除一个虚拟变量。 例如 –让我们考虑性别有两个值男性(0 或 1)和女性(1 或 0) 的情况。包括两个虚拟变量可能会导致冗余,因为如果一个人不是男性,在这种情况下该人是女性,因此,我们不需要在回归模型中使用这两个变量。这将保护我们免受虚拟变量陷阱的影响。