leetcode 15. 三数之和 - 点击直达
- leetcode 15. 三数之和 中等难度 双指针
- 1. 题目详情
- 1. 原题链接
- 2. 基础框架
- 2. 解题思路
- 1. 题目分析
- 2. 算法原理
- 3. 时间复杂度
- 3. 代码实现
- 4. 知识与收获

leetcode 15. 三数之和 中等难度 双指针
1. 题目详情
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000
-105 <= nums[i] <= 105
1. 原题链接
leetcode 15. 三数之和
2. 基础框架
● Cpp代码框架
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {}
};
2. 解题思路
1. 题目分析
( 1 ) (1) (1) 本题要求找出数组 n u m s nums nums中满足条件:三个位置都不同数 n u m s [ i ] + n u m s [ j ] + n u m s [ k ] = = t a r g e t nums[i]+nums[j]+nums[k]==target nums[i]+nums[j]+nums[k]==target的所有结果。
2. 算法原理
( 1 ) (1) (1) 首先想到暴力解法:先进行三层for循环遍历数组 n u m s nums nums,然后使用C++中set容器对结果进行去重处理,时间复杂度是 O ( n 3 ) O(n^3) O(n3)。
( 2 ) (2) (2) 在分析三数之和之前,我们先来看看两数之和为target时,如何在nums中寻找这两个数:
首先还是想到暴力解法:进行两层for循环,时间复杂度 O ( n 2 ) O(n^2) O(n2),如何优化呢?
使用对撞双指针算法:
先看张图吧:
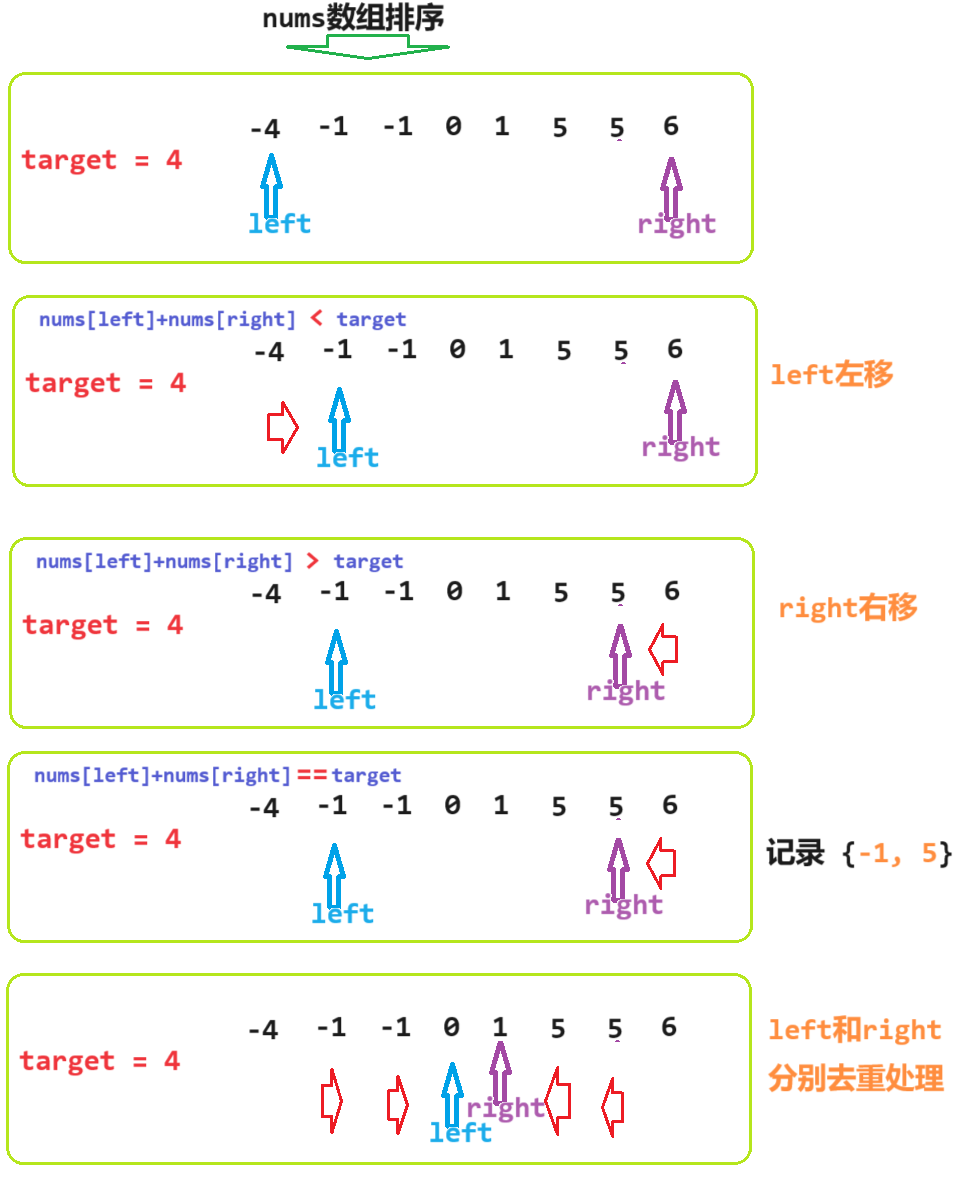
先对数组 n u m s nums nums进行快速排序, n u m s nums nums中就得到非递减的序列;
有序数组好就好在有序上,我们就可以找规律了:
左指针left指向第一个元素,右指针right指向最后一个元素。此时两个数的和 s u m = n u m s [ l e f t ] + n u m s [ r i g h t ] sum = nums[left] + nums[right] sum=nums[left]+nums[right] 注意这是一个有序数组,left指向的元素是[left, right]范围内最小的元素,right指向的元素是[left, right]中最大的元素。
sum的变化情况是:left向右移动时,sum不变或增大;right向左移动时sum不变或减小;
所以我们可以通过比较sum与target(本题target是0)的大小来确定移动的情况:
1.sum > target,想要趋近target则sum需要减小,所以移动右指针right;
2.sum < target,想要趋近target则sum需要增大,所以移动左指针left;
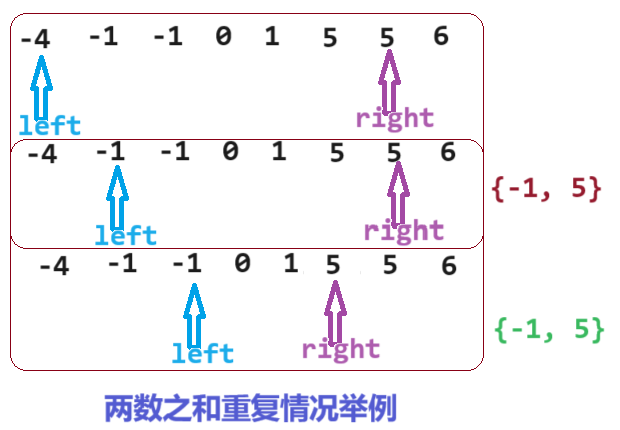
3.sum == target,得到了一个结果nums[left]和nums[right]。但是题目要求得到所有的结果,所以还需要继续,此时为了保证结果不重复,需要依据当前得到的结果进行去重处理(即当前已经有了结果nums[left],之后的出现的所有与nums[left]相同的元素都直接略过不在考虑,因为一定是结果中有的。right同理)
本题去重就是控制left和right跳过所有与自身重复的元素,这里需要注意的是控制left++或right--时需要先判断left或right是否越界,因为在极端情况下所有元素都相同,指针一直移动导致越界(细节细节)。
( 3 ) (3) (3) 好了,现在我们来看三数之和,其实就是上文两数之和的变形。三数之和的题目要求 n u m s [ i ] + n u m s [ l e f t ] + n u m s [ r i g h t ] = = t a r g e t nums[i]+nums[left]+nums[right]==target nums[i]+nums[left]+nums[right]==target(本题target为0),变形为 n u m s [ l e f t ] + n u m s [ r i g h t ] = = t a r g e t − n u m s [ k ] nums[left]+nums[right]==target-nums[k] nums[left]+nums[right]==target−nums[k],把target-nums[i]整体当做新的target,记为newtarget,所以得到 n u m s [ l e f t ] + n u m s [ r i g h t ] = = n e w t a r g e t nums[left]+nums[right] == newtarget nums[left]+nums[right]==newtarget。

( 4 ) (4) (4) 具体做法就是在两数之和的基础上在加上一层循环,遍历数组nums,每次确定一个nums[i],即确定一个newtarget。内层双指针left和right在范围[i+1, n-1]内以newtarget为目标进行寻找。
在本次循环结束时需要额外在做的一点是对nums[i]也要进行进行去重处理,同时也需要进行是否越界访问的判断(细节细节),至于为什么要进行去重,原理和两数之和做法类似。
( 5 ) (5) (5)
3. 时间复杂度
O ( n 2 ) O(n^2) O(n2)
外层循环每次确定一个目标值,内层循环在目标值之后的区间内寻找满足两数之和条件的结果。
3. 代码实现
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> vvi;// 排序sort(nums.begin(), nums.end());int n = nums.size();for(int i = 0; i < n;){// 两数之和int l = i + 1, r = n - 1;while(l < r){int sum = nums[l] + nums[r];int target = -nums[i];if(sum > target) r--;else if(sum < target) l++;else{vvi.push_back({nums[i], nums[l], nums[r]});l++;r--;//去重while(l < r && nums[l] == nums[l - 1]) l++;while(l < r && nums[r] == nums[r + 1]) r--;} }// 去重i++;while(i < n && nums[i] == nums[i - 1]) i++;}return vvi;}
};
4. 知识与收获
( 1 ) (1) (1) 三数之和是两数之和的变形,理解了两数之和的核心思想,三数之和也就能够顺理成章的解决。
( 2 ) (2) (2) 理解为什么需要去重处理:
对于两数之和(a+b=target):一个组合(a, b)满足了条件,数组又是有序的,对于a来说,以后的所有与其相同的数如果也满足了条件,那么一定会与(a,b)组合相同;对于b来说与a同理。
对于三数之和(a+b+c=target):变形为(a+b=target-c),target确定,本次循环内c也确定
T h e The The E n d End End