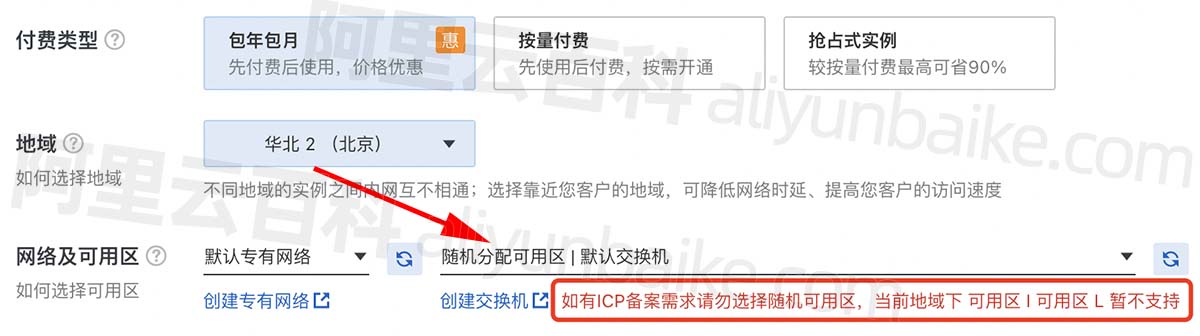
这篇博客将介绍堆的概念以及堆的实现。
1. 堆的定义:
首先堆的元素按照是完全二叉树的顺序存储的。
且堆中的某个节点总是不大于或不小于其父节点的值。
根节点最大的堆叫做大堆,根节点最小的堆叫小堆。逻辑结构如下图所示:
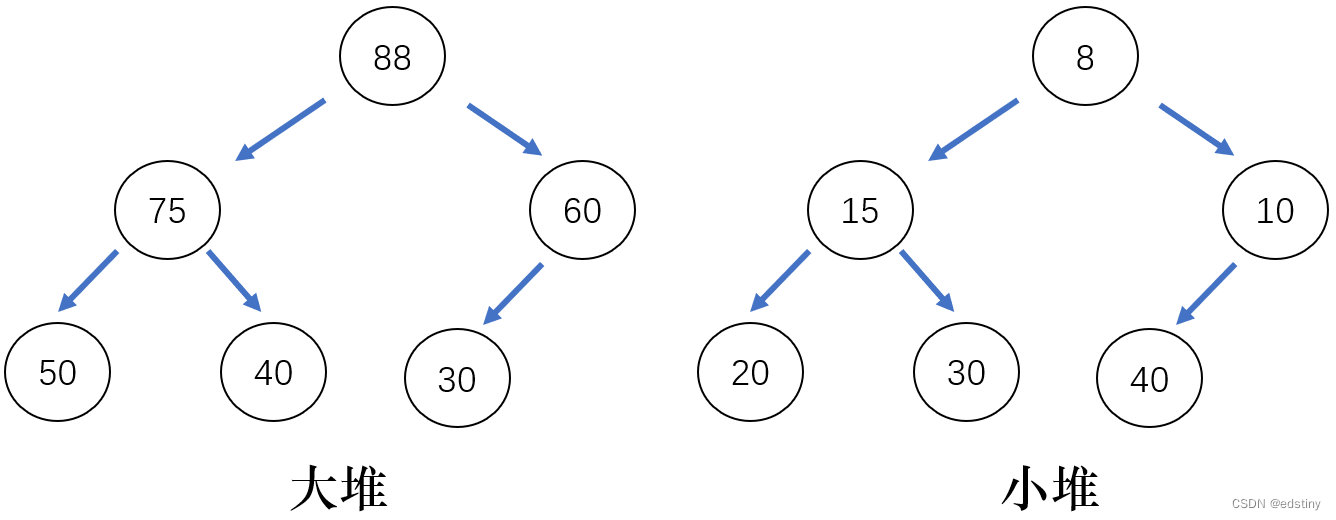
大堆和小堆的存储方式是利用一个一维数组进行存储的,其物理存储结构如下:
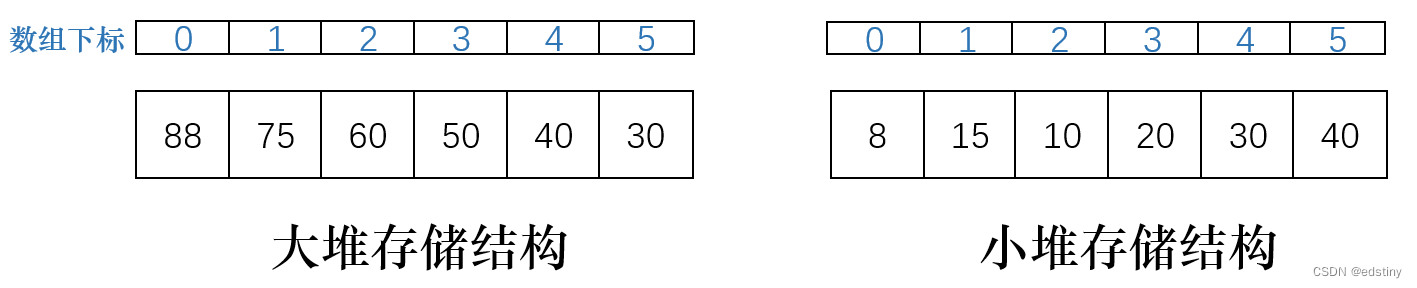
因此我们可以利用数组的下标,通过子节点找到父节点,或通过父节点找到子节点,其关系如下:
parent = ( child - 1 ) / 2; child = parent * 2 + 1;
2. 堆的创建
那么,现在我们有一个数组 a[] = {8, 1, 4, 5, 3, 2}; 在逻辑上可以看成一个完全二叉树,但是它还不是一个堆,我们要如何将其构建成一个堆呢?这里我们以构建一个小堆为例,我们从倒数第一个非叶子节点的子树开始调整,一直调整到根节点的树,就可以调整成堆,示意图如下:
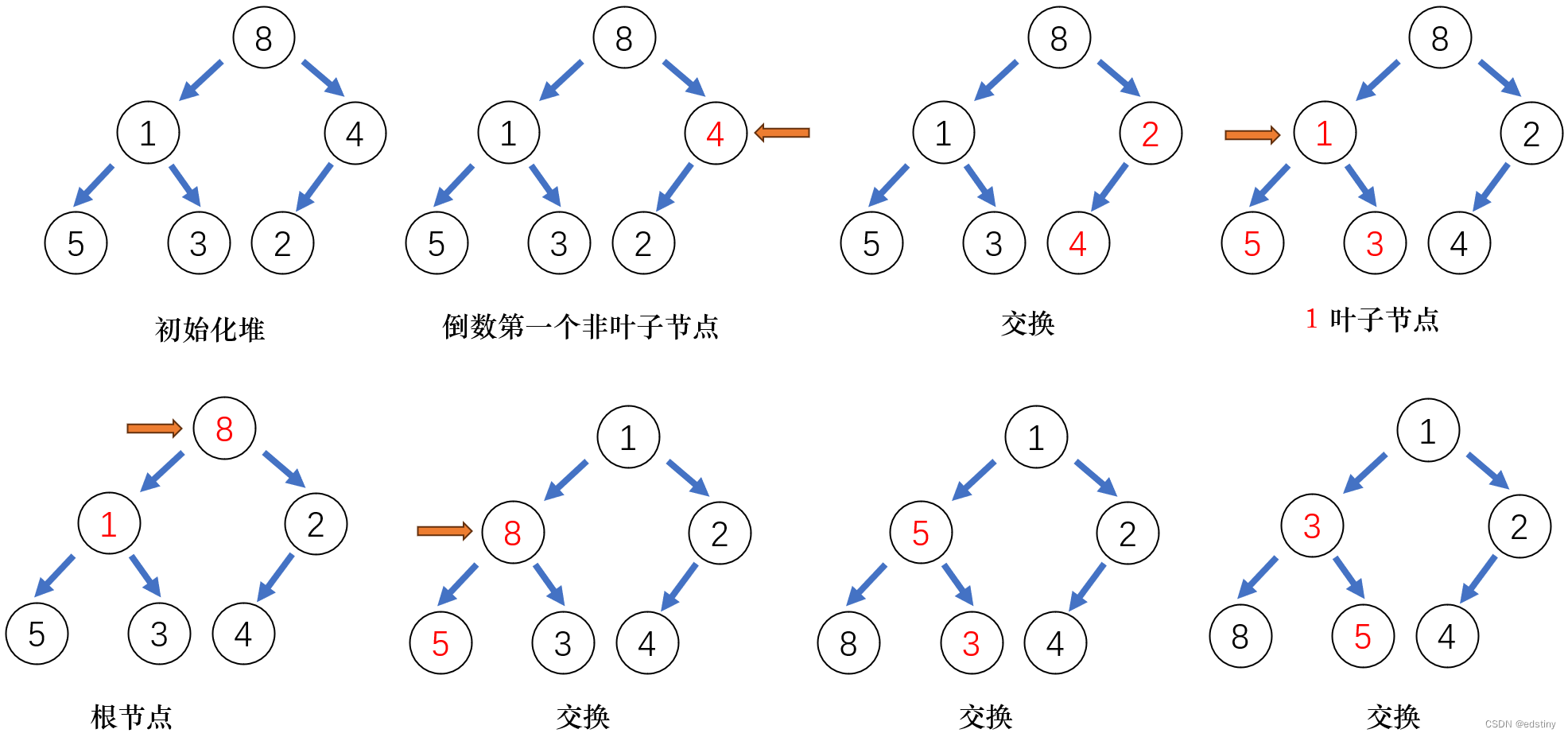 3. 堆的插入
3. 堆的插入
堆的插入一般插入到数组尾部,在进行向上调整算法,直到满足堆的定义 ,示意图如下:
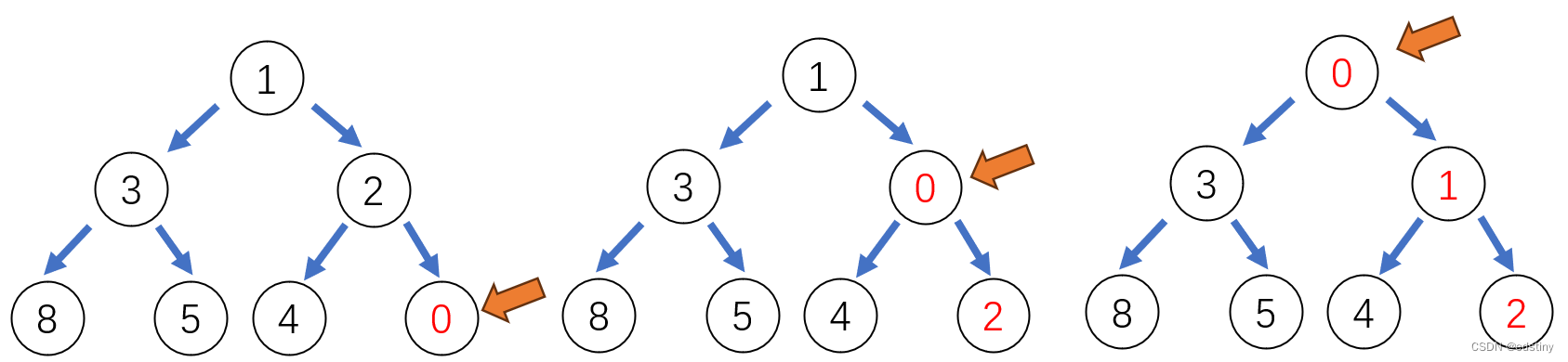
4. 堆的删除
堆的删除是删除堆顶的数据,将堆顶的根数据与最后一个数据交换,在删除数组的最后一个元素,在进行向下调整堆。示意图如下:
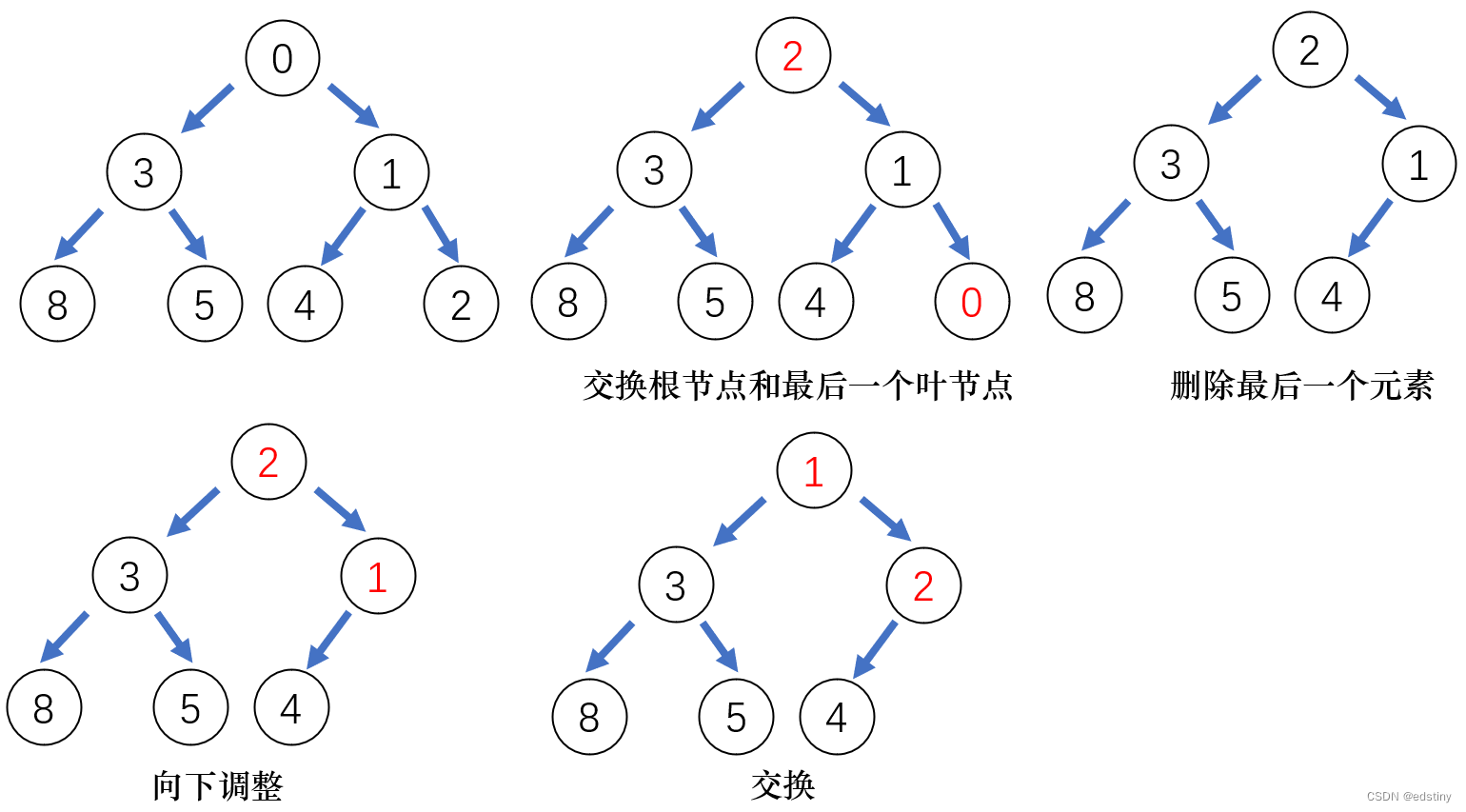
5. 代码实现
typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;void HeapInit(HP* php);//堆的初始化
void HeapDestroy(HP* php);//内存释放
void HeapPush(HP* php, HPDataType x);//堆的创建
void HeapPop(HP* php);//删除根节点
HPDataType HeapTop(HP* php);//返回根节点
bool HeapEmpty(HP* php);//判空
int HeapSize(HP* php);//堆大小
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->capacity = 0;php->size = 0;
}void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = 0;php->capacity = 0;
}void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}void Adjustup(HPDataType* a, int child)//小堆调整
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void HeapPush(HP* php, HPDataType x)
{if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail");return;}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;Adjustup(php->a, php->size-1);
}void AdjustDown(int* a, int n, int parent)//前提:左子树和右子树是大/小堆
{int child = parent * 2 + 1;while (child < n){//选出左右孩子中 小/大 的那个if (child+1 < n && a[child + 1] < a[child])//右孩子可能不存在{child++;}if (a[parent] > a[child]){Swap(&a[parent],&a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapPop(HP* php)//删除堆顶的数据
//首尾数据交换,再删除,再调堆
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->size-1]);php->size--;AdjustDown(php->a,php->size,0);
}HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}int HeapSize(HP* php)
{assert(php);return php->size;
}
6. 结果
完全二叉树:
int a[] = { 8,1,4,5,3,2 };
建堆:
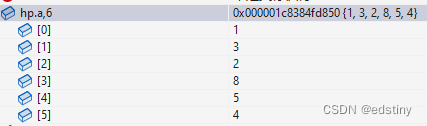
打印根节点,删除根节点,内存释放:
while (!HeapEmpty(&hp))
{int top = HeapTop(&hp);printf("%d\n", top);HeapPop(&hp);
}HeapDestroy(&hp);



 3. 堆的插入
3. 堆的插入