一.题目描述
小明冒充 X 星球的骑士,进入了一个奇怪的城堡。
城堡里边什么都没有,只有方形石头铺成的地面。
假设城堡地面是 n×n 个方格。如下图所示。
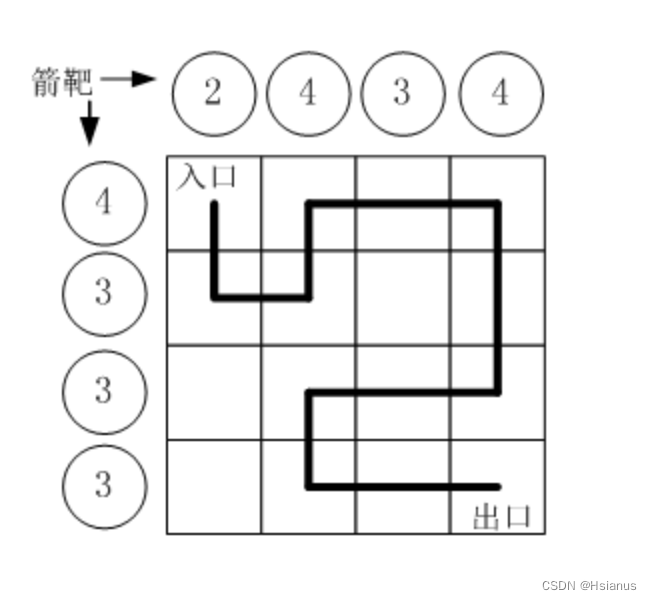
按习俗,骑士要从西北角走到东南角。可以横向或纵向移动,但不能斜着走,也不能跳跃。每走到一个新方格,就要向正北方和正西方各射一箭。(城堡的西墙和北墙内各有 n个靶子)同一个方格只允许经过一次。但不必走完所有的方格。如果只给出靶子上箭的数目,你能推断出骑士的行走路线吗?有时是可以的,比如上图中的例子。
本题的要求就是已知箭靶数字,求骑士的行走路径(测试数据保证路径唯一)
二.输入描述
第一行一个整数 N (0≤N≤20),表示地面有 N ×N 个方格。
第二行 N 个整数,空格分开,表示北边的箭靶上的数字(自西向东)
第三行 N 个整数,空格分开,表示西边的箭靶上的数字(自北向南)
三.输出描述
输出一行若干个整数,表示骑士路径。
为了方便表示,我们约定每个小格子用一个数字代表,从西北角开始编号: 0,1,2,3
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
四.问题分析
运用深度优先搜索,依次探测四个方向可以走的路径,注意回退问题。
//路径之谜
#include <iostream>
#include <stack>
using namespace std;const int N=22;
int n,row[N],col[N];
int map[N][N]={0};
bool flag=false;
stack <int> s;struct di{int x;int y;
};struct di d[4]={{1,0},{0,1},{-1,0},{0,-1}};void dfs(int x,int y){map[x][y]=1;row[y]--;col[x]--;if(x==n&&y==n){int cnt=0;for(int i=1;i<=n;i++)cnt=cnt+row[i]+col[i];if(cnt==0){flag=true;s.push(n*(x-1)+y-1);return;}}for(int i=0;i<4;i++){//试探方向if(map[x+d[i].x][y+d[i].y]==0&&row[y+d[i].y]>=1&&col[x+d[i].x]>=1&&!flag){dfs(x+d[i].x,y+d[i].y);}}if(!flag){map[x][y]=0;row[y]++;col[x]++;}else{s.push(n*(x-1)+y-1);}
}int main(int argc, const char * argv[]) {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;for(int i=0;i<N;i++)map[0][i]=map[i][0]=map[N-1][i]=map[i][N-1]=-1;for(int i=1;i<=n;i++)cin>>row[i];for(int i=1;i<=n;i++)cin>>col[i];dfs(1,1);while(!s.empty()){cout<<s.top()<<' ';s.pop();}return 0;
}