目录
介绍:
模板:
题目一(合根植物):
代码:
题目二(蓝桥幼儿园):
代码:
题目三(小猪存钱罐):
代码:
题目四(星球大战):
代码:
介绍:
并查集(Disjoint-set Data Structure),也称为不相交集合数据结构,用于解决集合的合并与查询问题。
并查集主要支持两个操作:
1. 合并(Union):将两个不相交的集合合并成一个集合。
2. 查询(Find):查询元素所在的集合。并查集可以用于解决一些集合相关的问题,例如判断两个元素是否属于同一个集合,求集合中的元素个数等。
并查集的实现通常使用数组和树结构。数组表示每个元素的父节点,树结构表示集合的层次结构。在进行查找操作时,通过递归或迭代找到根节点;在进行合并操作时,将一个集合的根节点连接到另一个集合的根节点上。
并查集的时间复杂度主要取决于合并和查询操作的路径长度,通常可以达到近似常数时间复杂度。
例如,假设有5个元素分别为1、2、3、4、5,初始时每个元素都是一个单独的集合:
[1, 2, 3, 4, 5]执行合并操作:将元素1和元素2合并
[2, 2, 3, 4, 5]执行合并操作:将元素2和元素3合并
[2, 2, 2, 4, 5]执行查询操作:查询元素1所在的集合
2执行查询操作:查询元素4所在的集合
4并查集是一种简单且高效的数据结构,可以在解决某些集合问题时提供方便和效率。
模板:
int find(int x)//查找
{if (f[x] == x) return x;return f[x] = find(f[x]);
}
void merge(int x, int y) //合并
{x = find(x), y = find(y);if (x != y)f[x] = f[y];
}题目一(合根植物):

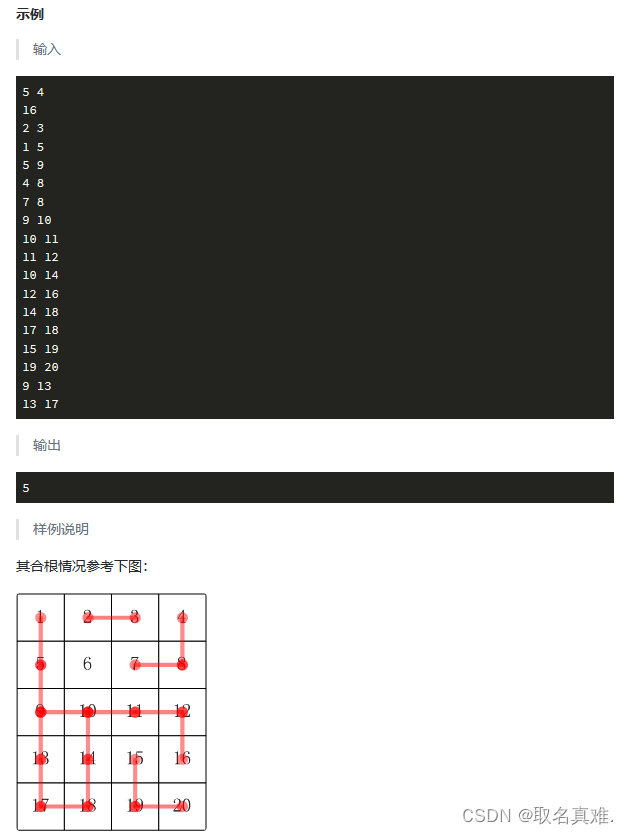
代码:
#include<iostream>
using namespace std;
int f[1000010];
int find(int k)//查询父亲
{if (f[k] == k)return k;else{f[k] = find(f[k]);return f[k];}
}
void merge(int a, int b)//合并
int main()
{int n, m;cin >> n >> m;for (int i = 1; i <= n * m; i++)//初始化{f[i] = i;}int k;cin >> k;while (k--){int a, b;cin >> a >> b;merge(a, b);//合并}long long ans=0;for (int i = 1; i <= n * m; i++){if (f[i] == i)//父亲为自己则为一个集合的代表ans++;}cout << ans;
}题目二(蓝桥幼儿园):

代码:
#include<iostream>
using namespace std;
int n,m;
int f[200100];
int find(int x)//查找
{if(f[x]==x)return x;return f[x]=find(f[x]);
}
void merge(int x,int y)//合并
{x=find(x),y=find(y);if(x!=y)f[x]=f[y];
}
int main()
{cin>>n>>m;for(int i=1;i<=n;i++)//初始为自己f[i]=i;while(m--){int x,y,z;cin>>z>>x>>y;if(z==1)//操作一合并{merge(x,y);}else//操作二{if(find(x)==find(y))cout<<"YES"<<endl;elsecout<<"NO"<<endl;}}
}题目三(小猪存钱罐):
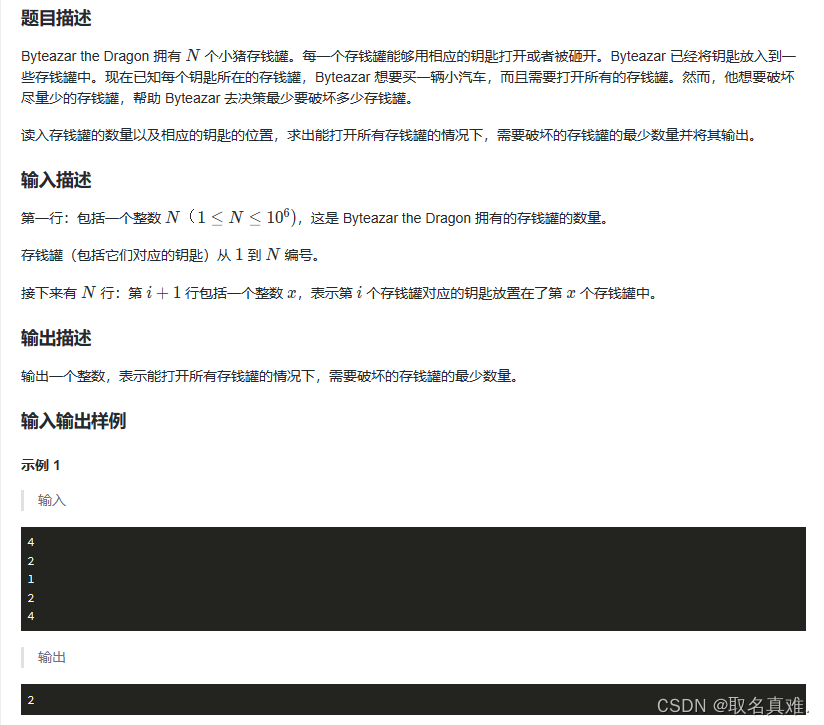
代码:
#include <iostream>//实际上就是几个连通分支
using namespace std;
int n,ans=0;
int f[1001000];
int find(int x)//查找
{if (f[x] == x) return x;return f[x] = find(f[x]);
}
void merge(int x, int y) //合并
{x = find(x),y = find(y);if (x != y) f[x] = f[y];
}
int main()
{cin>>n;for(int i=1;i<=n;i++)f[i]=i;for(int i=1;i<=n;i++){int x;cin>>x;merge(x,i);}for(int i=1;i<=n;i++){if(f[i]==i)//有一样的则为一个集合里的ans++;}cout<<ans;
}题目四(星球大战):


代码:
#include<iostream>
#include<vector>
using namespace std;
int n, f[500100], ans[500100], m, k,cnt=0;
vector<int> e[500100];
int destroys[500100];
int broken[500100];
int find(int x)//查找
{if (f[x] == x) return x;return f[x] = find(f[x]);
}
void merge(int x, int y) //合并
{x = find(x),y = find(y);if (x != y) f[x] = f[y];
}
int main()
{cin >> n >> m;while (m--){int x, y;cin >> x >> y;e[x].push_back(y), e[y].push_back(x);}cin >> k;for (int i = 0; i < k; i++){cin >> destroys[i];broken[destroys[i]] = 1;//标记为摧毁}for (int i = 0; i < n; i++)//初始化父亲点为自身f[i] = i;for (int i = 0; i < n; i++){if (broken[i])//被摧毁则跳过continue;for (int j = 0; j < e[i].size(); j++)//遍历i点相连的边{int tmp = e[i][j];//相邻的点if (broken[tmp])//被摧毁跳过continue;merge(i, tmp);//合并两点为同一连通块}}for (int i = 0; i < n; i++)//遍历所有城市,先找到所有摧毁完后的连通块数if (!broken[i] && find(i) == i)//该城市没被摧毁且不是自身为父亲节点cnt++;for (int i = k - 1; i >= 0; i--)//从后往前修复道路{ans[i] = cnt;//记录该城市还没被修复时的连通块数量broken[destroys[i]] = 0;//修复该点cnt++;//修复该点,可以成为一个独立的连通分支for (int j = 0; j < e[destroys[i]].size();j++)//遍历该摧毁点的相连边{int v = e[destroys[i]][j];//相邻的点if (!broken[v] && find(v) != find(destroys[i]))//该城市没被摧毁且二者之前不属于同一连通块{merge(v, destroys[i]), cnt--;//因为原本相连,其实二者为同一连通块,合并二者且连通数减一}}}cout << cnt << endl;//完整时的连通块数量for (int i=0;i<k;i++)cout << ans[i] << endl;}