一.作用
强连通分量可以判断环和进行缩点。还有一系列作用....
这篇文章介绍缩点
二.题目
https://www.luogu.com.cn/problem/P2341
三.思路
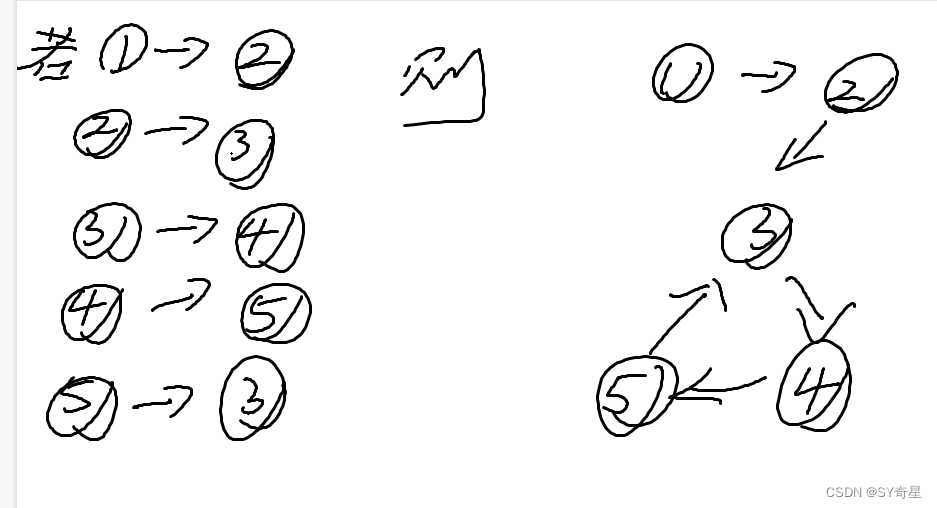
我们分析可以知道当一个点没有出度时,则为最受欢迎的牛。但如果有多个出度,则没有最受欢迎的牛。
这是只有一个出度的情况:
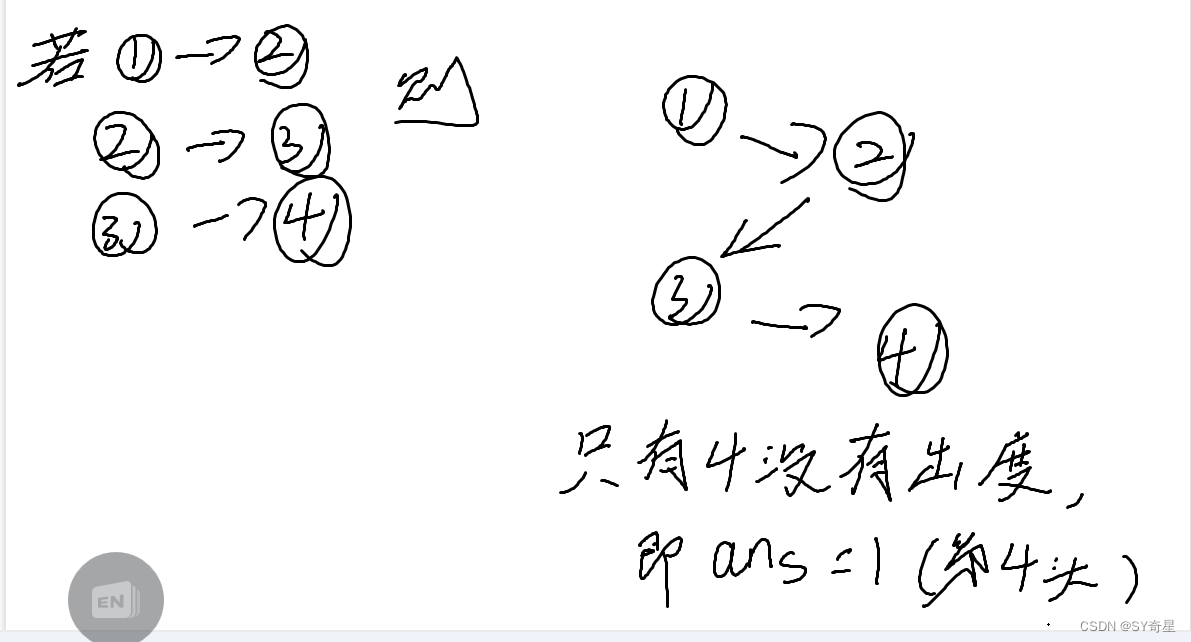
这是多个出度的情况:
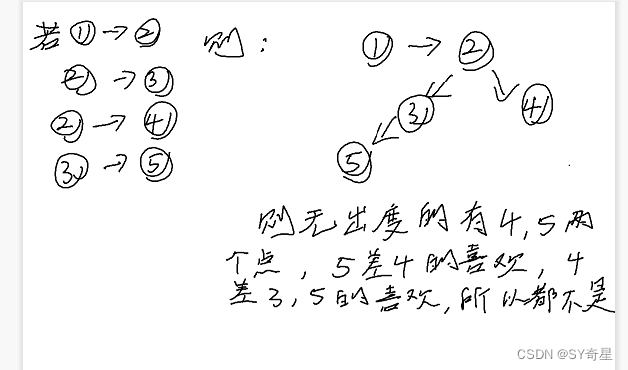
但为什么要判断环&&对环缩点呢?
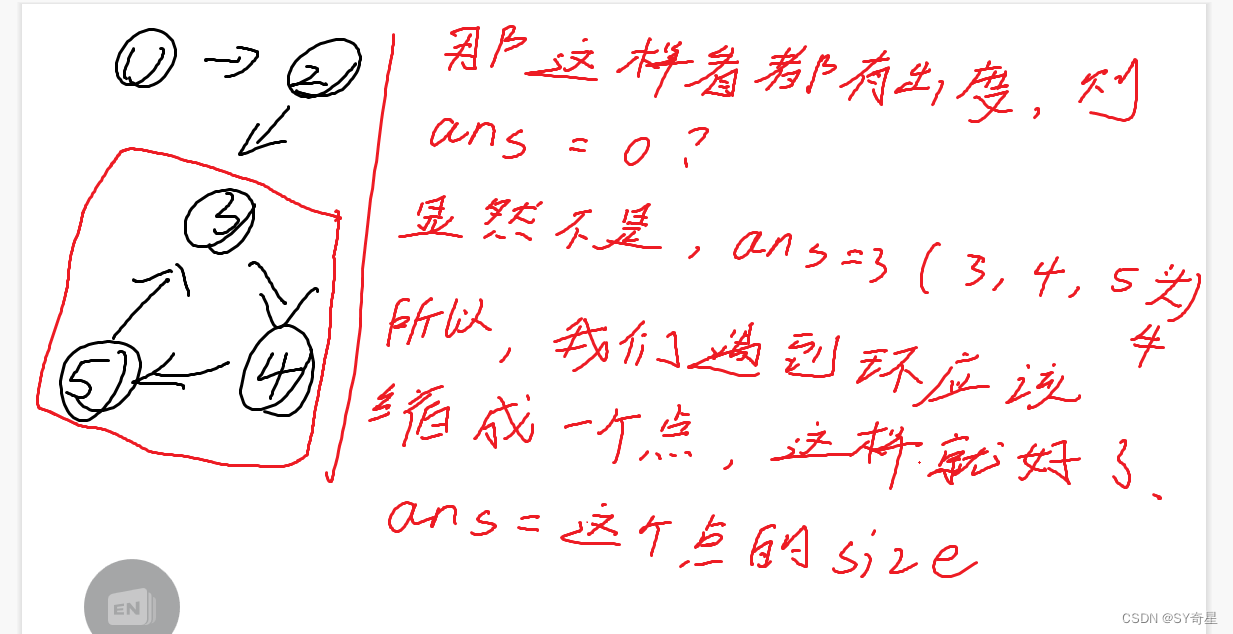
四.代码实现
只是微改,基础是
【图论】强连通分量_SY奇星的博客-CSDN博客
#include<bits/stdc++.h>
#define maxn 50005
using namespace std;
int n,m;
int head[maxn],cnt;
struct Edge{int u,v,next;
}edge[maxn];
void add(int u,int v){edge[++cnt]=(Edge){u,v,head[u]}; head[u]=cnt;
}
vector<int> it[maxn];
int ls,l[maxn],out[maxn];//有多少环 ,这个数属于哪个环,点的出度
int dfn[maxn],low[maxn],tot;
int sta[maxn],ins[maxn],top;
void tarjan(int u){dfn[u]=low[u]=++tot;sta[top++]=u;ins[u]=1;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(dfn[v]==0){tarjan(v);low[u]=min(low[u],low[v]);}else if(ins[v]){low[u]=min(low[u],dfn[v]);}}int j=0;if(dfn[u]==low[u]){ls++;while(1){j=sta[--top];ins[j]=0;it[ls].push_back(j);l[j]=ls; //缩点, 即一个点属于哪个环,或者说是哪个缩点。 if(u==j) break;}}
}
int main(){scanf("%d%d",&n,&m);int u,v;for(int i=1;i<=m;i++){scanf("%d%d",&u,&v);add(u,v);}for(int i=1;i<=n;i++){if(dfn[i]==0) tarjan(i);}for(int i=1;i<=n;i++){for(int j=head[i];j;j=edge[j].next){int v=edge[j].v;if(l[i]!=l[v]){out[l[i]]++; //出度 }}}int ans=0;for(int i=1;i<=ls;i++){if(out[i]==0){if(ans==0) ans=i;else{cout<<0; return 0;} }}cout<<it[ans].size();return 0;
}