总言

  主要内容：编程题举例，理解滑动窗口的思想。（是什么？什么时候用？为什么能用？时间复杂度？如何写代码？）
  
  

  
  
  
  

1、滑动窗口

  1）、总述
  滑动窗口算法是一种在数组或链表上解决问题的常见策略，它的核心思想是通过维护一个固定大小或大小变动的窗口来高效地解决问题。滑动窗口本身是一种抽象概念，在应用中可以有不同的表现形式和实现方法，但其核心都围绕着在数据序列上维护一个滑动的“窗口”来展开。
  
  2）、基本思想
  简单来讲可概括为入窗口、判断何时出窗口、更新结果。

  初始化窗口： 通常，窗口的初始位置和大小是根据问题的要求来设定的。窗口的大小可以是固定的，也可以是变化的，但在这个讨论中，我们主要关注固定大小的窗口。
  窗口滑动： 窗口在数据序列上从左到右滑动，每次滑动时，窗口内的元素会发生变化。这通常涉及到移除窗口最左边的元素和添加窗口最右边的元素。
  计算或更新： 在窗口滑动的过程中，根据问题的要求，计算或更新与窗口相关的某些值或状态。
  结果输出： 在滑动过程中，可能会在某些特定位置（如窗口的起始位置或结束位置）记录结果或进行某种判断，也可能在整个滑动过程结束后输出结果。
  
  3）、实现方法
  双指针法： 这是实现滑动窗口的常见方法。使用两个指针（通常称为“左指针”和“右指针”）来定义窗口的边界。左指针和右指针可以在数据序列上同向移动，从而改变窗口的大小和位置。
  数据结构辅助： 根据问题的需要，可能会使用额外的数据结构（如哈希表、队列等）来辅助实现滑动窗口算法。
  
  
  4）、优点和注意事项
  优点： 滑动窗口算法通常能在O(n)的时间复杂度内解决一些问题，因为它避免了不必要的重复计算。通过滑动窗口的思想，我们可以在处理数据序列问题时获得更高的效率，特别是在需要处理连续子序列或固定大小子序列的问题时。
  注意事项： 在实现滑动窗口算法时，需要注意窗口的边界条件和数据的更新逻辑，以确保算法的正确性。此外，对于特定问题，可能需要根据问题的特性来设计和优化滑动窗口算法。

  
  
  通常：在OJ题中，可以通过对暴力解法进行优化，从而确定是否使用滑动窗口，以及如何使用。
  
  

2、长度最小的子数组（medium）

  题源：链接。

  
  

2.1、暴力求解

  1）、思路说明
  暴力求解即遍历数组，穷举所有满足条件的情况，比较获取长度最小的子数组。
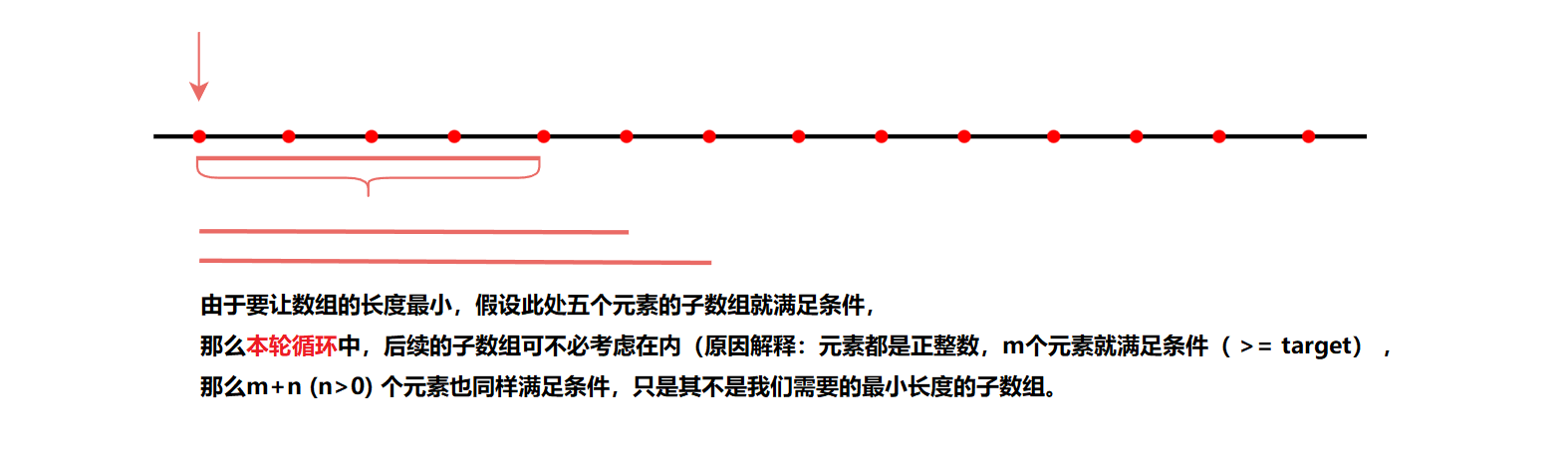
  具体说明：对任意一元素，固定其为起始位置，从该位置开始往后找一段最短的区间，使该段区间的和>=target。从左到右，获取所有元素作为起始位置所得的结果，从中找出最小值。

  
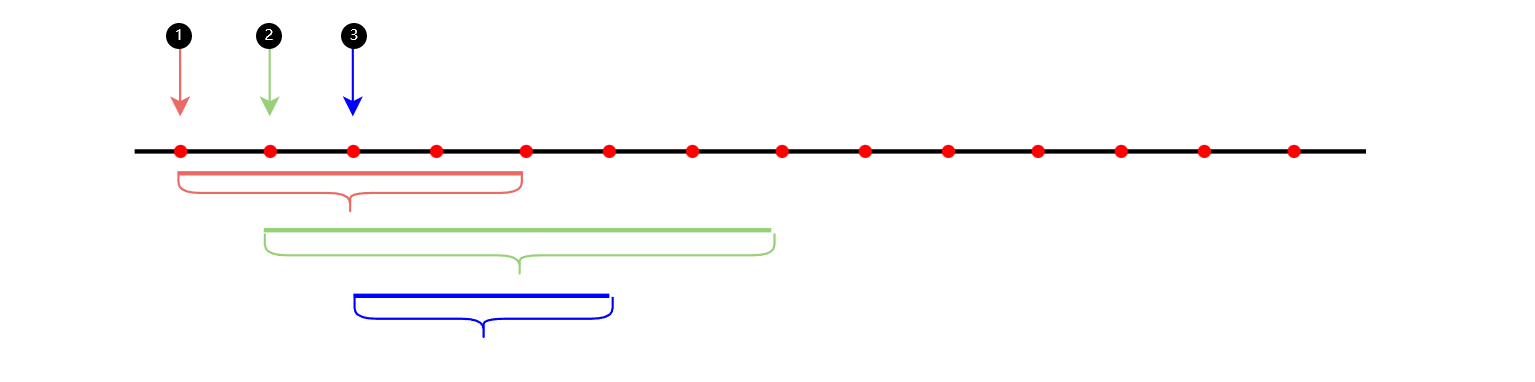
  其它：注意这里对最下长度的理解。

  
  
  2）、题解
  时间复杂度：$O(n^2)$

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int ret = INT_MAX;//保存最终结果int n = nums.size();for (int start = 0; start < n; start++)// 枚举出所有满⾜和⼤于等于 target 的⼦数组[start, end]，这里只需要长度最小的情况{int sum = 0; // 记录从这个位置开始的连续数组的和for (int end = start; end < n; end++)// 寻找结束位置{sum += nums[end]; // 将当前位置加上if (sum >= target) // 当这段区间内的和满⾜条件时{ret = min(ret, end - start + 1);// 更新结果，以当前start元素开头的最短区间已经找到break;}}}// 返回最后结果：判断是否找到return ret == INT_MAX ? 0 : ret;}
};

  
  
  
  

2.2、滑动窗口

  滑动窗口是对暴力解法的优化处理。理解如何从暴力解法到滑动窗口的解法（为什么能用），相比于直接使用滑动窗口（如何用）更重要。
  此外，滑动窗口的解法过程（入窗口、出窗口、判断、更新数值等等）正是依赖于对暴力解法的分析。若对其过程写不出来，可回到暴力解法重新推导。
  
  
  1）、优化过程分析：

  回顾上述暴力解法，初始时，left、right的位置，固定left，向右挪动right，找[left,right]该区间内满足和>=target的最小区间。

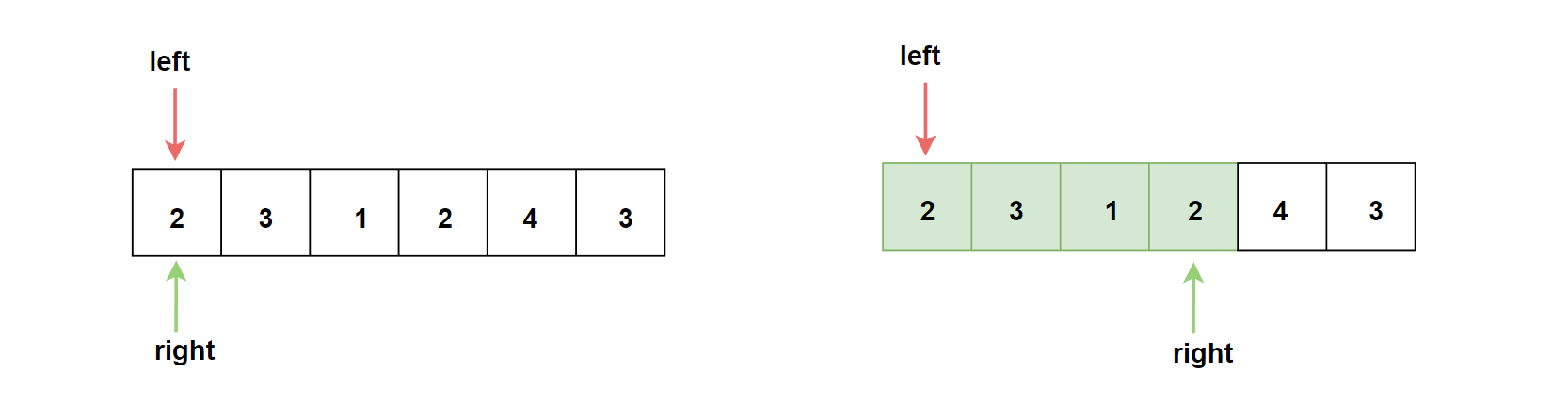
  这样一回合结束后，以元素2为left的最短区间结果已经出来。让left++，right回到left起始位置处，继续新一轮遍历寻找（下图左）。
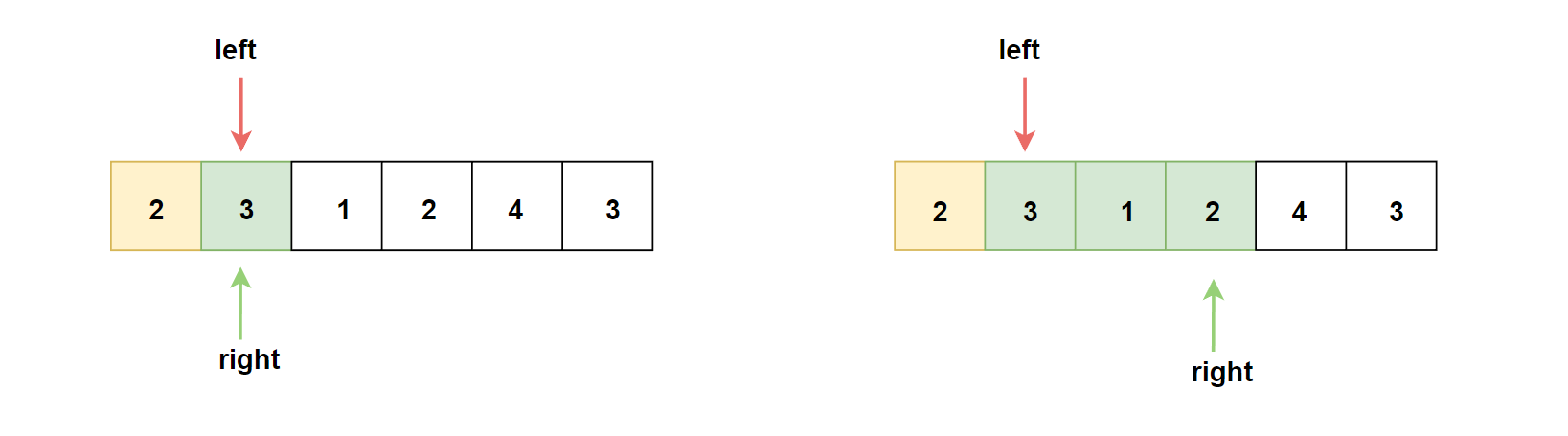  我们可在此步骤优化（上图右），实际right没有返回到left指向位置处重新遍历的必要。在经过上一回合后，left++到下一元素位置，此时[left,right]区间内的值之和只有两种情况：①仍旧满足条件（>=target），这意味着新回合中的最小区间已经找到；②不满足条件（<target），说明元素不够，可以让right++扩大区间范围，即重复寻找操作。

  如此，既能同暴力解法一致，找到每回合的最小区间值，又能省去一定数量上重复无效遍历的操作（以上图为例，right从3位置处往后遍历，此过程中[left,right]达不到条件，最终right仍旧回到原先指向的2位置处），达到了优化的目的。像此类做法，使用了滑动窗口的思想。
  
  
  2）、总结：
  使用滑动窗口的思想再叙述总结一遍：

  1、初始化： left = 0 ，right = 0，初始化双指针，让其充当窗口的左端点和右端点。sum=0，用于统计窗口内的元素之和，进行后续条件判断。
  2、何时入窗： right指向的元素添加进入sum中，意味着当前元素入窗。
  3、根据条件进行判断（是否出窗or继续入窗）： 比较sum和target进行条件判断。① 若sum < target不满足条件， right++，让下⼀个元素进入窗 ；②若sum >= target 满足条件，更新结果，并且将左端元素划出窗口（此时，对应的sum元素和要一并同步）。此时，需要继续判断是否满足条件，并更新结果（根据上述分析可知，left++到下一元素位置时仍旧可能满足条件）
  4、何时更新输出结果： 在出窗前进行更新。
  
  
  
  3）、题解：

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int ret = INT_MAX;//用于记录最小长度，赋值是为了判断输出结果int sum = 0;//用于统计子区间元素和for(int left =0, right = 0; right < nums.size(); ++right){sum += nums[right];//入窗while(sum >= target) //满足条件，更新结果，结束本回合。（使用while是因为left++后情况有二，可能仍旧满足条件，故要循环判断）{ret = min(ret, right - left + 1);//注意这里下标与长度的关系sum -= nums[left++];//先将left指向的元素从sum中移除，再让left右移继续新回合}//来到此处，说明不满足条件，此时继续入窗（这里是for循环，++right的操作写在了末尾循环体中）}return ret == INT_MAX ? 0 : ret;}
};

  
  
  
  
  
  
  

3、无重复字符的最长子串(medium)

  题源：链接。

  
  

3.1、暴力求解+哈希表

  1）、思路说明
  总述： 方法类似，从某一字符位置为起始，往后寻找无重复字符的子串，记录其长度。遍历字符串，枚举出所有满足条件的子串，比较得出最长子串。

  补充说明：
  1、如何判断某一字符是否重复？ 由于s 由英文字母、数字、符号和空格组成。在往后寻找无重复子串能到达的位置时，可以利用哈希表统计出字符出现的频次，从而判断子串是否出现重复元素。int hash[128] = { 0 };

  2、 ASCII码可以表示的字符个数是128个字符。（后128个称为扩展ASCII码）。 前128个为常用的字符如运算符，字母，数字等。32～126（共95个）是字符（32是空格），其中48～57为0到9十个阿拉伯数字；65～90为26个大写英文字母，97～122号为26个小写英文字母，其余为一些标点符号、运算符号等。
  
  
  2）、题解

class Solution {
public:int lengthOfLongestSubstring(string s) {int ret = 0; // 记录当前长度for (int left = 0; left < s.size(); ++left) // 枚举从不同位置开始的最⻓重复⼦串{int hash[128] = {0}; // 创建⼀个哈希表，统计频次for (int right = left; right < s.size(); ++right){hash[s[right]]++;       // 统计该字符出现的频次if (hash[s[right]] > 1) // 说明表中元素重复{break;//当前回合的最长无重复子串已找到，可以开始下一回合。}ret = max(ret, right - left + 1); // 如果没有重复，就更新 ret}}return ret; // 返回结果}
};

  
  
  

3.2、滑动窗口

  1）、过程分析：
  滑动窗口的方法建立在暴力求解之上。

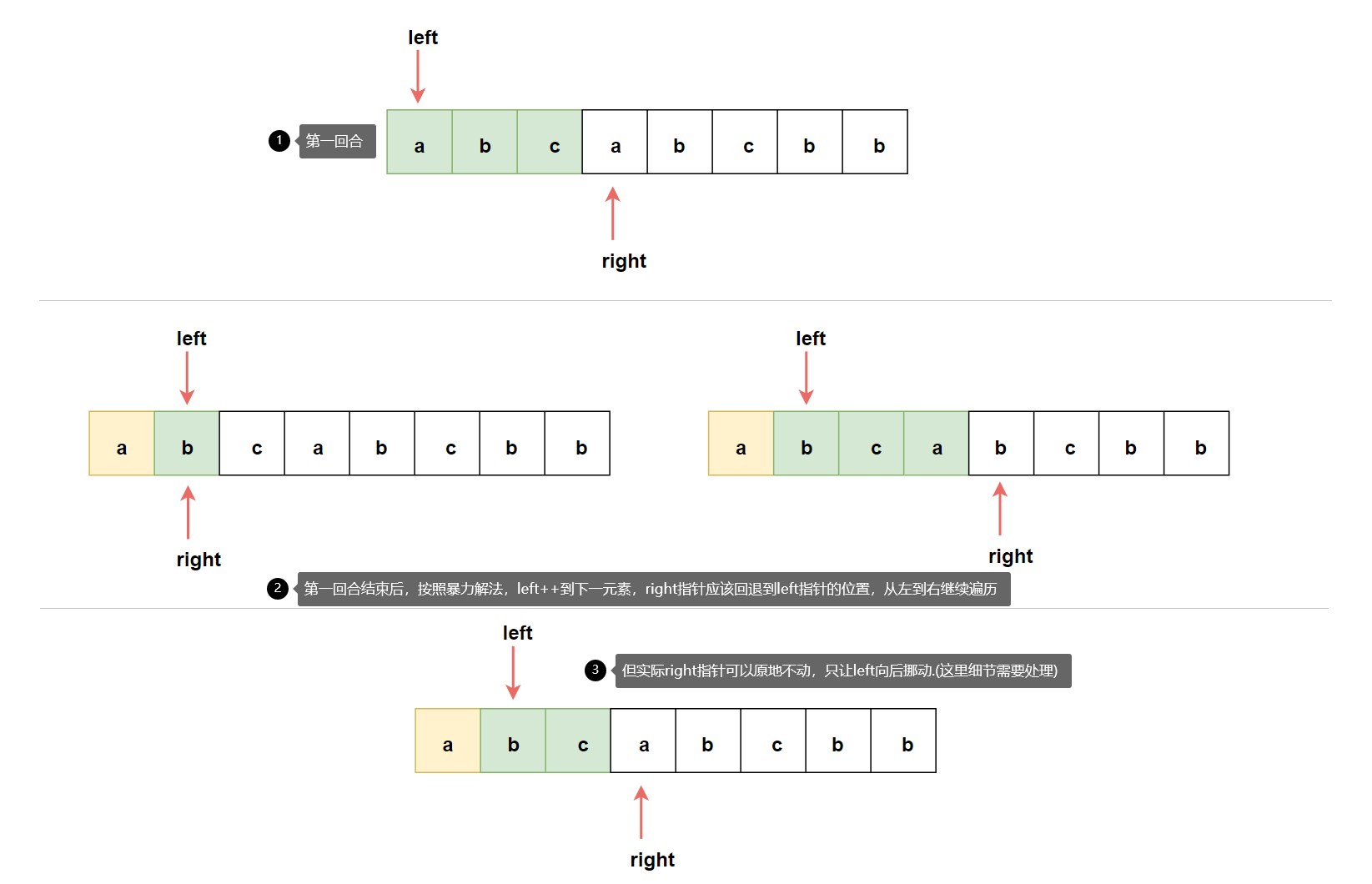
  细节说明： left向右移动时，并非一次只跨越一步。我们是根据hash表来进行判断的。实际需要让hash表中重复字符的频率下降到1以下才行。

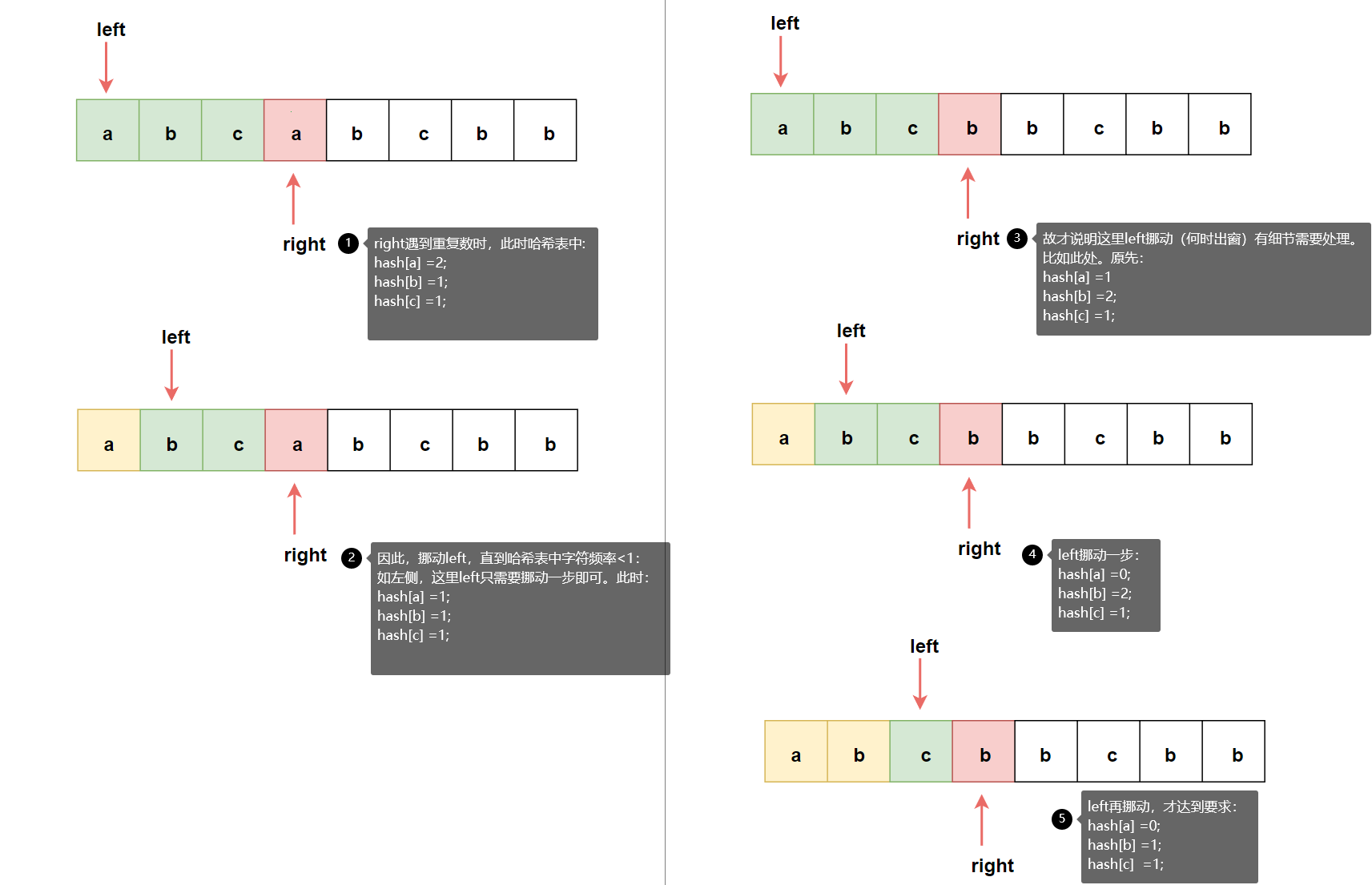
  在暴力解法中，设n为s中某一字符，right指向字符n的位置，hash[n]可能出现三种情况：
  1、hash[n] == 0，说明[left,right]该区间内没有字符n的存在，此时将该字符统计入哈希表中，right向右。hash[n] == 1。
  2、hash[n] == 1，说明[left,right]该区间内出现字符n的存在。此时再遇到字符n，将有hash[n] > 1。则在此之前的=区间为当前回合的最长不重复区间。
  3、hash[n] > 1 / hash[n] ==2，说明left,right]该区间内有重复元素，此时应该让left指针向右挪动，从而使得移动过程中哈希表在做减操作（hash[left]--），直到 n 这个元素的频次变为 1。

  
  

  2）、总结：
  使用滑动窗口的思想再叙述该过程：
  1、初始化： left = 0 ，right = 0，初始化双指针，让其充当窗口的左端点和右端点。ret=0，用于记录每回合的输出结果。
  2、何时入窗： right指向的元素ch添加进入哈希表中，意味着当前元素入窗。
  3、根据条件进行判断（是否出窗or继续入窗）： 比较哈希表中字符ch的频次。① 如果没有超过 1 ，说明当前窗口没有重复元素，可以直接更新输出结果；②如果这个字符出现的频次超过 1 ，说明窗口内有重复元素，那么就从左侧开始划出窗口，直到 ch 这个元素的频次变为 1 ，然后再更新输出结果。
  4、何时更新输出结果： 在条件判断后就可以进行更新。
  
  
  
  3）、题解：
   时间复杂度：$O(n)$

class Solution {
public:int lengthOfLongestSubstring(string s) {int ret =0;//用于记录最终输出结果int hash[128] = {0};for(int left = 0, right = 0; right < s.size(); ++right){hash[s[right]]++;//入窗口while(hash[s[right]] > 1)//判断是否有重复数{--hash[s[left++]];//先减去哈希表中left指向的元素，再让left后移（出窗⼝）}ret = max(ret, right - left +1);//更新输出结果//让下⼀个元素进⼊窗⼝（for循环，这里写在了末尾循环体中）}return ret;}
};

  使用while循环的写法：

class Solution {
public:int lengthOfLongestSubstring(string s) {int hash[128] = {0}; // 使⽤数组来模拟哈希表int left = 0, right = 0, n = s.size();int ret = 0;while (right < n) {hash[s[right]]++;                 // 进⼊窗⼝while (hash[s[right]] > 1)        // 判断hash[s[left++]]--;            // 出窗⼝ret = max(ret, right - left + 1); // 更新结果right++;                          // 让下⼀个元素进⼊窗⼝}return ret;}
};

  
  
  
  
  
  

4、最大连续 1 的个数Ⅲ(medium)

  题源：链接。

  
  

4.1、暴力求解+计数器

  1）、思路说明
  同理，先用暴力解法对此题进行分析。 虽然题目要求翻转为0，但实际并不用真实翻转，这样做后续反倒要恢复数组原状，徒增麻烦。我们可以使用一点“虚”的操作，题目只要求返回一个长度，那么完全可以用一个计数器来统计遍历过程中 0 出现的次数，模拟翻转过程即可。 换句话说，可以对题目做一个转换：给你一个数组，要求找出一个最长子数组，该子数组满足最多只含有k个0的条件。

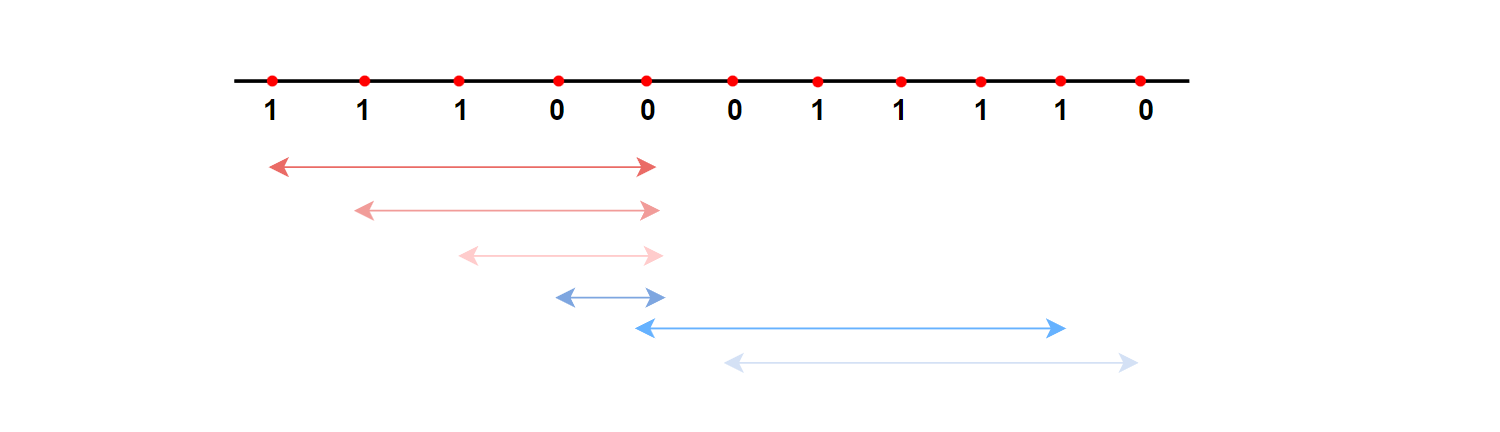
  细节点：注意分析此题，题目说最多可翻转 k 个 0，即翻转次数在k以内均满足要求，并不一定要每回合都翻转k个0 （这一点关系到[left, right]的长度统计，每次 right 向右挪动时，只要满足计数器<=k，就是一次有效挪动，需要更新此段区间长度）。
  
  
  2）、题解

class Solution {
public:
int longestOnes(vector<int>& nums, int k) {int len = 0; //用于记录最终长度int size=nums.size();for (int left = 0; left < size; ++left) {if (k >=size) { len = size; break; }//优化操作1：若是翻转0的个数大于总数组，那就没必要继续进行查找了，直接返回数组总长度即可if(size-left <= len){break;}//优化操作2：当前回合中，剩余的元素数量小于len，就不用再遍历了，因为不可能找到大于len的长度。int count = 0;  //统计0个数的计数器,每次外循环开始时重新计算int right =left;while(right < size && count <=k){if(nums[right]== 0)count ++;if(count <= k) //这里需要注意，count只要<=K就满足要求，不一定必须填充k个0{len = max(len , right - left +1);//更新当前区间长度right ++;//后移继续}}}return len;
}
};

  
  
  

4.2、滑动窗口

  1）、思路说明
  同理进行优化。right指针不必每次都返回到left处，实际当[left、right]区间内0的个数超标时，right是不会向后挪动的，而left一直向左挪动，所得到的这段区间只会越来越小，直到0的个数不超过 k 个。

  
  
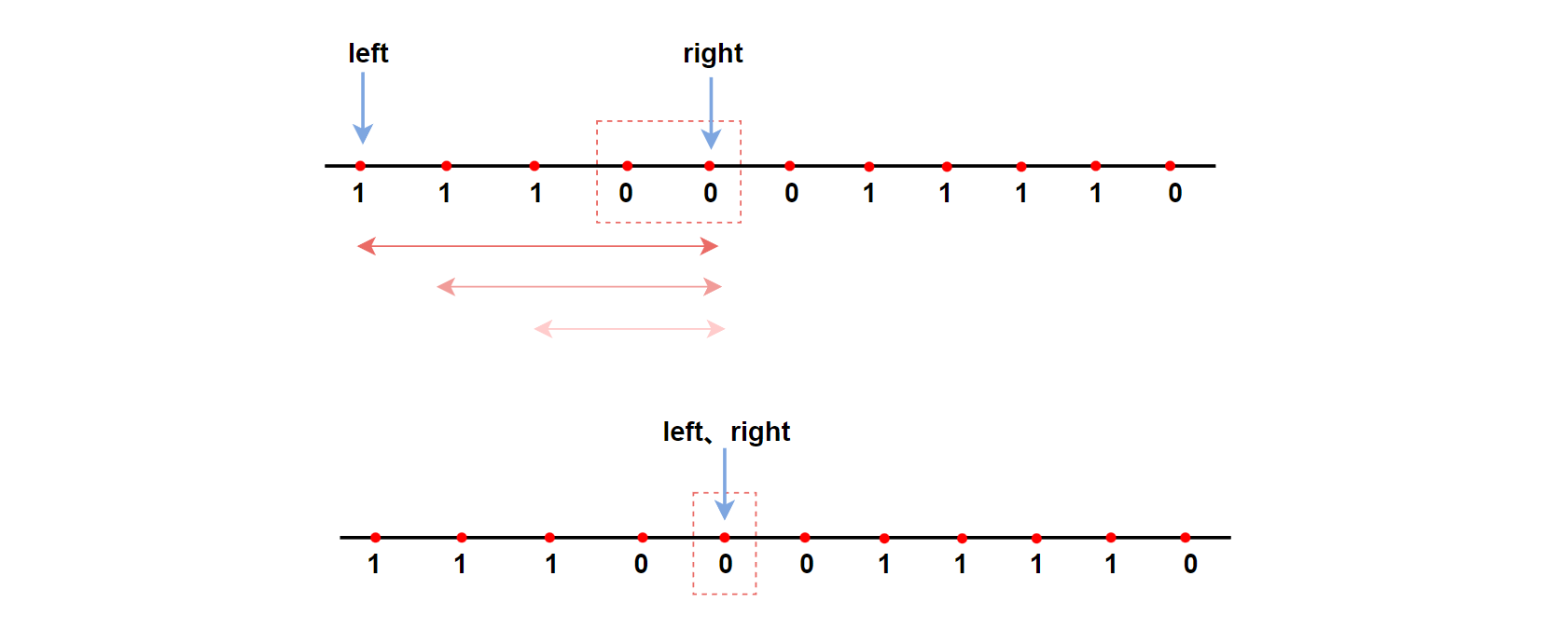
  1、初始化： left = 0 ，right = 0，初始化双指针，让其充当窗口的左端点和右端点。count=0，用于记录0元素的个数。ret = 0，用于记录输出结果。
  2、何时入窗： 让right指针指向的元素入窗，判断此处入窗元素是否为0。若是，则count++，否，则count计数器不变。
  3、根据条件进行判断（是否出窗or继续入窗）： 判断计数器count中0是否超标。如果超标，依次让左侧元素滑出窗口，恢复count中的计数，直到 0 的个数不超标为止；
  4、何时更新输出结果： 新元素入窗后，若满足count的条件，可以进行ret的更新。
  
  
  2）、题解
  时间复杂度：$O(n)$

class Solution {
public:int longestOnes(vector<int>& nums, int k) {int ret = 0;// 用于记录输出结果int count =0;// 用于统计0的次数for(int left =0, right = 0; right < nums.size(); ++right){//入窗：判断right指向是否为0，若为0则count计数，不为0则不用处理if(nums[right] == 0) count++;while(count > k)// 条件判断。先判断left指向的是否为0，再出窗。{if(nums[left]==0)count--;left++;}ret = max(ret,right - left +1);//更新输出结果}return ret;}
};

  
  
  
  
  

5、将x减到0的最小操作数(medium)

  题源：链接。

  
  

5.1、暴力求解（正难则反）

  1）、思路说明
  分析本题，若直接枚举数组左端、右端两段连续的、和为 x 的最短数组，稍微有些不易理清。解题学中有一个重要的思维方法：“正难则反”，当从问题的正面去思考问题，遇到阻力难以下手时，可以通过逆向思维，从问题的反面出发，逆向地应用某些知识去解决问题。

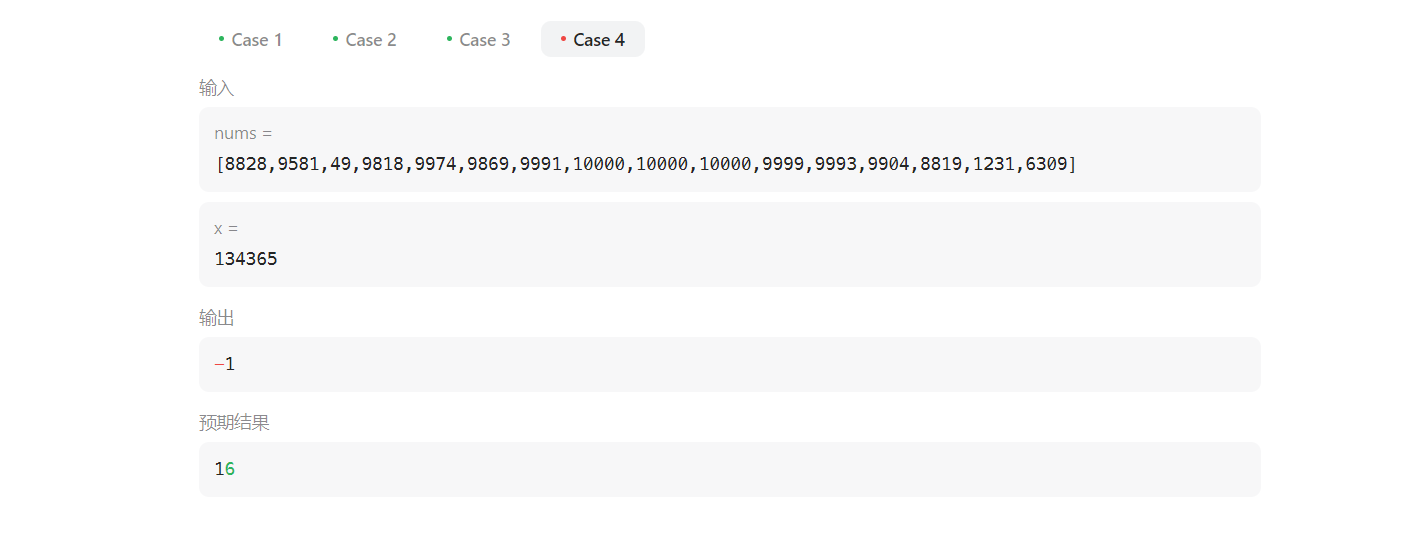
  此题我们可以转换一下，既然两端分别的区间不易枚举，那么夹在中间的这段连续的区间呢？

  如下图，若数组总元素之和是 $sum$，题目要求不断移除数组最左边或最右边的元素，使之和为 $x$，也就意味着A + C 段的元素和为 $x$ ，即中间B段的元素和为$sum-x$ 。因要最小操作数， A + C 段要尽可能小，即B段尽可能大。

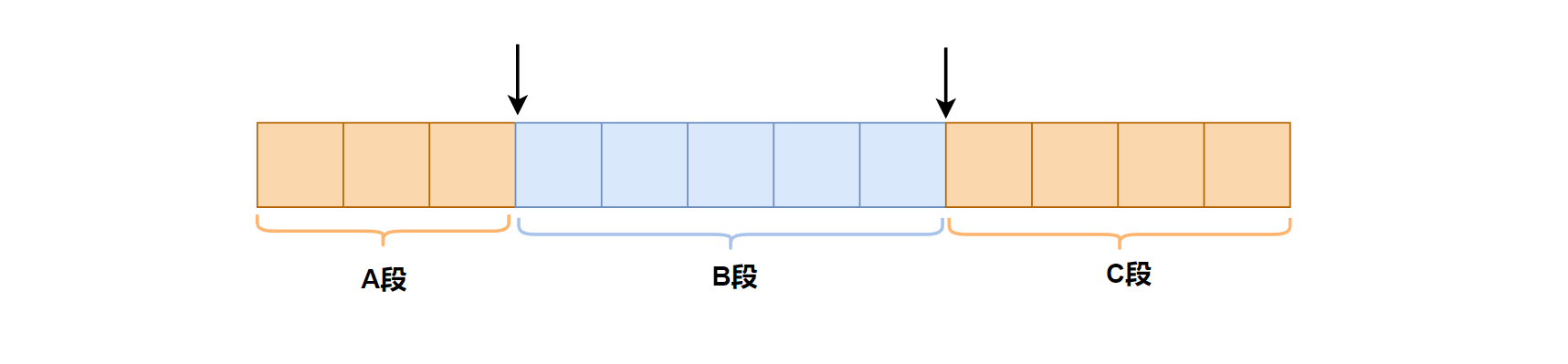
  因此，此题就能转换为：求数组内一段连续的、和为 $sum-x$ 的最长子数组。如此就可以使用滑动窗口来求解，只不过这里我们仍旧先举例暴力解法。
  
  
  
  2）、题解
  效果与题一相同，故此处不做赘述。

class Solution {
public:int minOperations(vector<int>& nums, int x) {int ret = -1;//用于每回合输出结果//遍历：统计数组总和int sum = 0;for(auto e: nums){sum+=e;}if(x == sum) return nums.size();//处理1：所有元素之和加起来才满足x，此时target=0, ret = -1，与操作数不存在的情况无法区别，故这里做特殊处理。int target = sum - x;//中间区间的目标值if(target < 0 )  return -1;//处理2：存在所有数值和sum < x，此时target为负数，而数组均为整数，再怎么遍历都不可能为负。for(int i = 0; i < nums.size(); ++i){int total = 0;//用于统计当前回合中的总和for(int j = i; j < nums.size(); ++j){total+=nums[j];if(total == target){ret = max(ret, j - i + 1);break;}}}return ret == -1 ? ret : nums.size() - ret;}
};

  处理1的示例如下：$sum-x=0$，此时 $target=0$，而提示中 $1<=nums[i]<=10^4$ ，故这里if(total == target)条件进不去，导致最终ret = -1。

  
  
  

5.2、滑动窗口

  1）、思路说明
  这里从暴力求解到滑动窗口的优化逻辑与 「 题一：长度最小的子数组」相同，只是判断条件部分变为了sum == target，需要注意判断条件和输出结果是两个独立的部分，不要将二者混淆。
  
  1、初始化： left = 0 ，right = 0，初始化双指针，让其充当窗口的左端点和右端点，滑动窗口区间表示为[left,right)。 sum = 0，用于记录当前区间内元素之和。ret = 0，用于记录输出结果。
  2、何时入窗： sum+=nums[right]，表示该元素入窗。
  3、根据条件进行判断（是否出窗or继续入窗）： 判断sum和target，情况有三。①若sum < target，让right++继续入窗，直至变量和大于等于 target ，或右指针right已经移至头；②若sum > target，让左指针left--出窗，此时sum也要一并减去出窗元素，直至变量和小于等于target ，或左指针已经移至头；③ 若满足sum == target ，获取到当前最大长度，更新输出结果。

  4、何时更新输出结果： 满足sum == target 条件时才更新结果。
  
  
  2）、题解

class Solution {
public:int minOperations(vector<int>& nums, int x) {//获取数组总元素和int sum = 0;for(auto e: nums){sum+=e;}//计算目标值int target = sum - x;if(target < 0) return -1;int ret = -1;//记录每次输出结果int total = 0;//记录区间内元素总和for(int left = 0, right = 0; right < nums.size(); ++right){total += nums[right];//入窗while(total > target)//判断:出窗。当前left++后，total的值仍旧可能>target，因此这里要使用while循环判断total -= nums[left++];if(total == target)ret = max(ret, right -left +1);}return ret == -1 ? -1 : nums.size() - ret;//返回的是x的操作数，非target的操作数}
};

  
  
  
  
  

6、水果成篮（medium）

  题源：链接。

  
  

6.1、暴力求解+哈希表

  1）、思路说明
  本题题目有点阅读理解的意味，理解题目后可将题目要求转化为如下形式：从数组中寻找一个长度最长的连续区间(子数组)，使其中元素至多不超过两种。
  暴力求解同之前一样，以一侧为起始，往后寻找一段区间，使其中元素种类不超过2。遍历整个元素，枚举出符合要求的情况，比较获取最长区间。

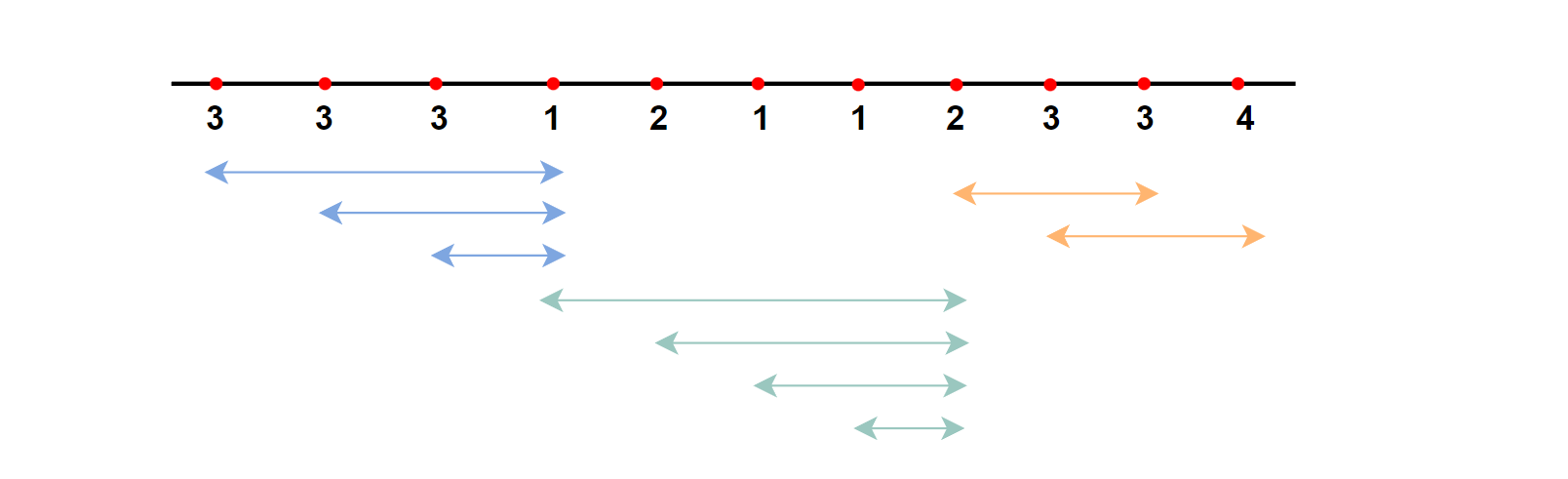
  这里有一个问题，如何判断当前子区间中的元素种类？
  回答：①可以借助哈希，诸如unordered_map此类容器（length > 2 ）。②当然，结合提示可知，$0<=fruits[i]<fruits.length=10^5$，这里也可以直接使用数组来提高速率（hash[100001] = {0}）。
  
  
  
  2）、题解
  这里演示了用unordered_map<int,int>做哈希的暴力解法：

class Solution {
public:int totalFruit(vector<int>& fruits) {int ret = 0;// 记录每回合输出结果for(int left = 0; left < fruits.size(); ++left){unordered_map<int,int> hash;// 统计出现了多少种⽔果for(int right = left; right < fruits.size(); ++right){hash[fruits[right]]++;if(hash.size() <= 2)// 符合条件时，每次都更新输出结果ret = max(ret, right - left +1);else break; //水果种类大于2时，不符合要求，不用再往后遍历}}return ret;}
};

  
  
  

6.2、滑动窗口

  1）、思路说明
  在暴力解法中，一回合结束后 left 右移，right 每次都要回退到 left 位置处。

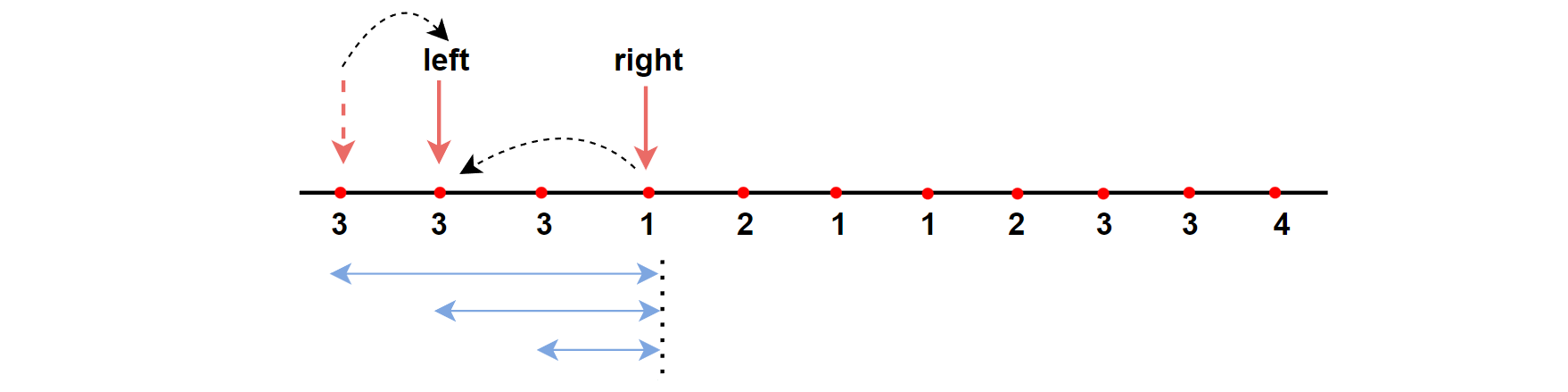
  我们可以在此处优化，当left右移时，[left, right]区间内元素种类kind可能存在两种情况：
  1、kind不变，此时right指针从left处重新遍历，仍旧会回到原先位置。此段[left, right]区间范围一直在缩小。

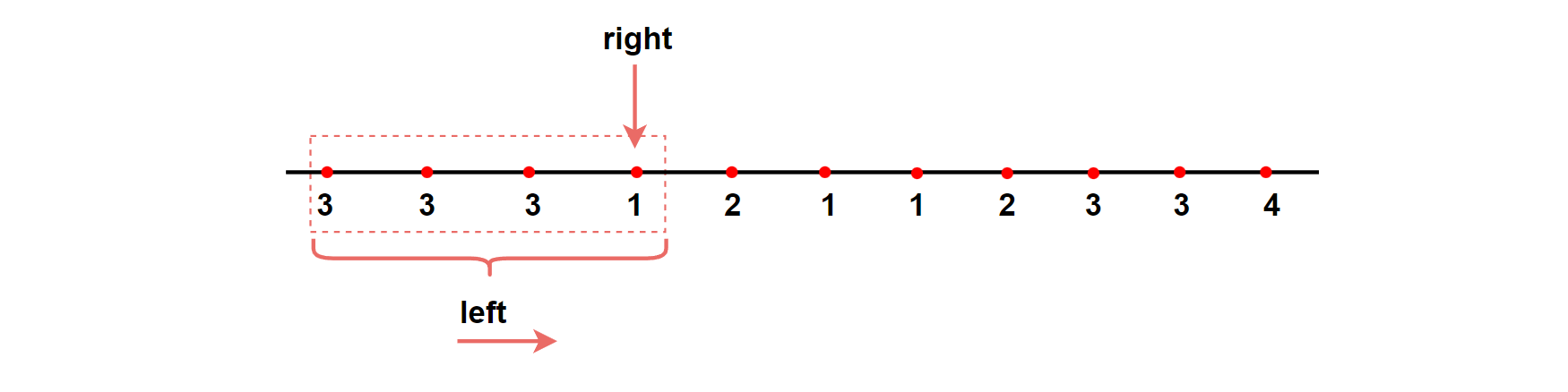
  2、kind减小，此时[left, right]区间内又可以容纳新的kind（right指针可右移）

  故可以使用「滑动窗口」思想来解决问题。
  1、初始化： left = 0 ，right = 0，初始化双指针，让其充当窗口的左端点和右端点。ret = 0，用于记录输出结果。初始化哈希表hash来统计窗口内水果的种类和数量（可以有两种写法）。
  2、何时入窗： 将当前水果放入哈希表中;，表示该元素入窗。
  3、根据条件进行判断（是否出窗or继续入窗）： 判断哈希表元素大小。①如果大小超过2，说明窗口内水果种类超过了两种。那么就从左侧开始依次将水果划出窗口，直到哈希表的大小（水果种类）小于等于2，然后更新结果ret；②如果没有超过2，说明当前窗口内水果的种类不超过两种，直接更新结果ret，right++，让下一个元素进入窗口。
  4、何时更新输出结果： 进行条件判断后，说明当前入窗元素合法，此时才更新结果。
  
  
  
  2）、题解
  使⽤容器做哈希表：

class Solution {
public:int totalFruit(vector<int>& fruits) {int ret = 0;unordered_map<int, int> hash; // 统计窗⼝内出现了多少种⽔果for (int left = 0, right = 0; right < fruits.size(); ++right) {hash[fruits[right]]++;  // 进窗⼝while (hash.size() > 2) // 判断{                       // 出窗⼝hash[fruits[left]]--;if (hash[fruits[left]] == 0)hash.erase(fruits[left]);left++;}ret = max(ret, right - left + 1); // 更新输出结果}return ret;}
};

  
  使用数组做哈希表：

class Solution {
public:int totalFruit(vector<int>& f) {int hash[100001] = {0}; // 统计窗⼝内出现了多少种⽔果int ret = 0;for (int left = 0, right = 0, kinds = 0; right < f.size(); right++) {if (hash[f[right]] == 0)kinds++;      // 维护⽔果的种类hash[f[right]]++; // 进窗⼝while (kinds > 2) // 判断{// 出窗⼝hash[f[left]]--;if (hash[f[left]] == 0)kinds--;left++;}ret = max(ret, right - left + 1);}return ret;}
};

  
  
  
  
  

7、找到字符串中所有字母异位词（medium）

  题源：链接。

  
  

7.1、暴力求解

  1）、思路说明
  1、如何理解这里的异位词？ 实则是给定字符串p中所有字符的排列情况。例如：若p="abc"，则它的异位词可以是$A_3^1=6种$ ：abc、acb、bac、bca、cab、cba。

  2、如何判断字符串s中找出的一组子串为p的异位词？
  ①可以先对两组字符串进行排序，然而逐一比较即可。（此方法下排序相对耗时：$n\ast logn$）
  ②一种方法是使用哈希表来判断。将s中取出的字符串放入hash1中，p中字符串放入hash2中。比较hash1、hash2中的字符个数是否相等。
  ③由于s 和 p 仅包含小写字母，因此可以用两个大小为26的数组来模拟哈希表，再引入一个变量count用于统计s中出现的有效字符（这里统计的是与p中字符种类、个数一一对应的字符。）
  
  
  3、暴力解法：根据上述，遍历s，每次取长度为p.size()的子串，比较是否为异位词，若是则记录下标，否则继续遍历寻找，直到s中长度为p.size()的所有子串都被遍历过为止。

  
  
  

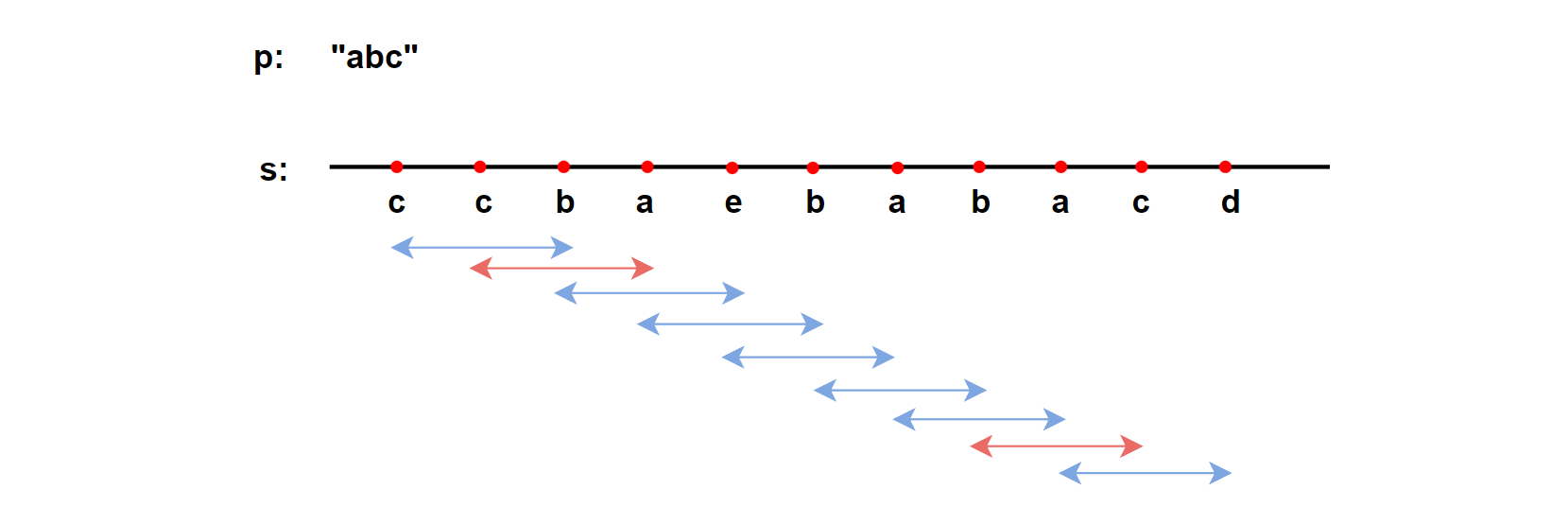
7.2、滑动窗口（固定长度的滑动窗口）

  1）、思路说明
  滑动窗口在暴力解法上进行了优化。一回合结束后，left++进入下一回合的遍历，因为[left,right]区间内有一断重复区域，right不用回退重新遍历。

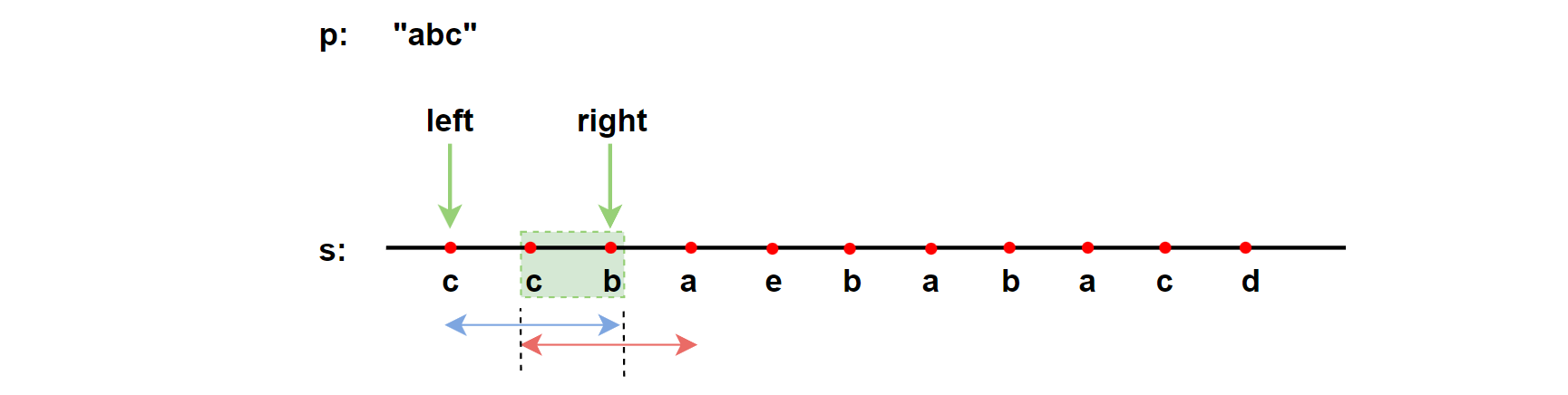
  因为字符串p的异位词的长度一定与字符串 p的长度相同，所以只用在字符串s中构造一个长度与字符串p的长度相同的滑动窗口，并在滑动中维护窗口中每种字母的数量即可。

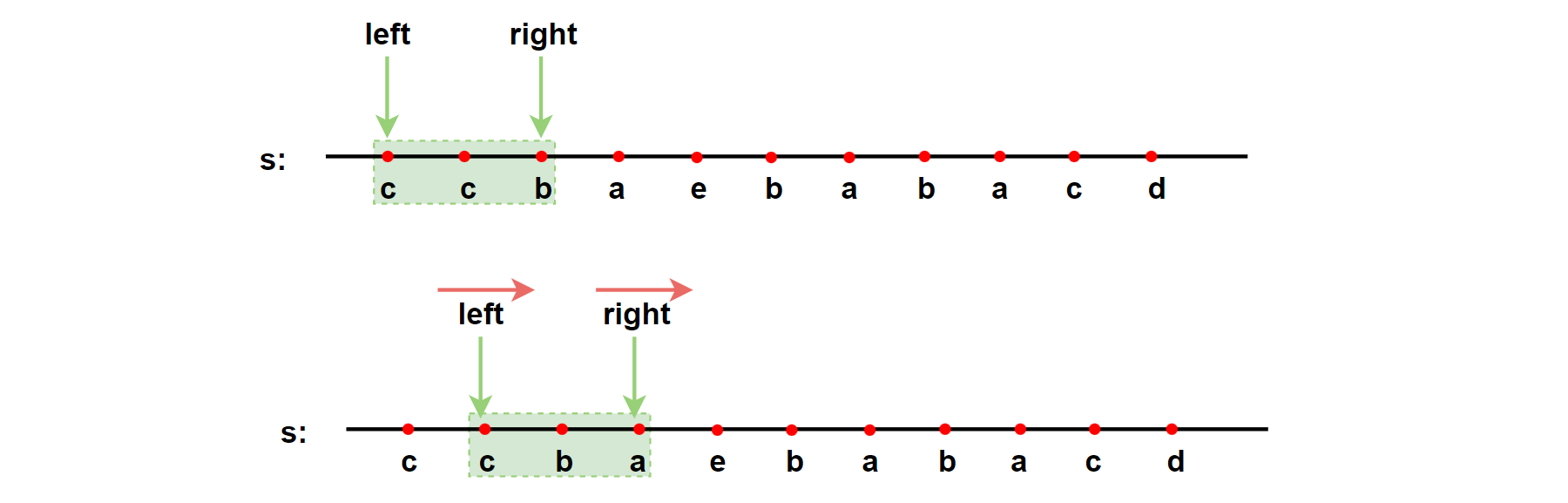
  剩余问题就是如何判断是否为异位词。（上述提到的三种，或者其余优化方法）
  
  
  2）、题解一
  使用hash1、hash2，对异位词的判断即比较两哈希表中的字符及其数目是否相同。（PS：这里也可以直接用数组替代容器）

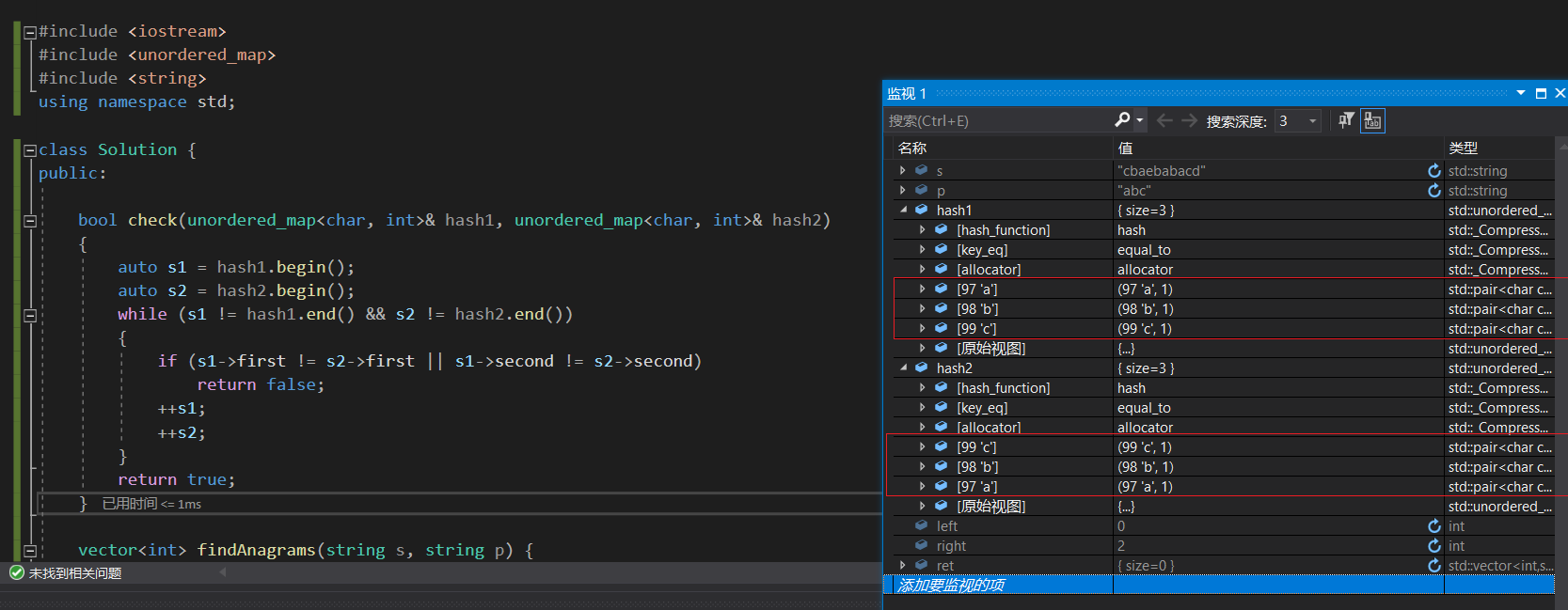
class Solution {
public:bool check(map<char,int>& hash1,map<char,int>& hash2){auto s1 = hash1.begin();auto s2 = hash2.begin();while(s1!=hash1.end() && s2 !=hash2.end()){if(s1->first != s2->first || s1->second != s2->second)return false;++s1;++s2;}return true;}vector<int> findAnagrams(string s, string p) {map<char,int> hash1,hash2;for(auto& e: p){hash1[e]++;}vector<int> ret;//用于记录输出结果for(int left = 0, right = 0; right < s.size(); ++right){hash2[s[right]]++;if( right - left + 1 > p.size()){hash2[s[left]]--;if(hash2[s[left]] == 0)hash2.erase(s[left]);left++;}if(right - left + 1 == p.size()){if(check(hash1,hash2))ret.push_back(left);}}return ret;}
};

  关于不使用unordered系列容器说明：该系列容器无序，如果要比较判断则check(hash1,hash2)需要换一种实现方式。

  
  
  
  3）、题解二
  使用上述第三种方法对异位词进行判断。维护一个变量count，用于记录hash2中，与hash1匹配的有效字符。

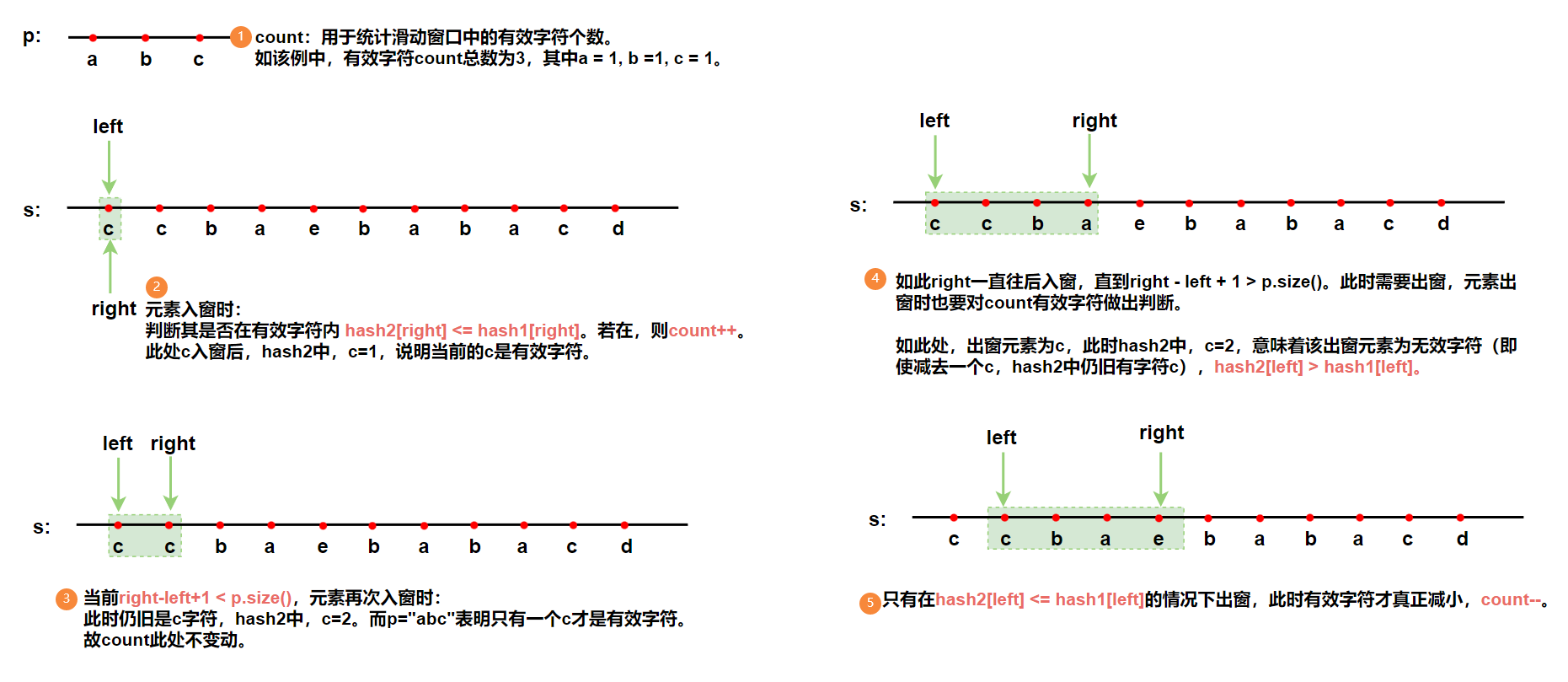
class Solution {
public:vector<int> findAnagrams(string s, string p) {int hash1[26] ={0};// 统计字符串 p 中每个字符出现的个数int hash2[26]= {0};// 统计窗⼝⾥⾯的每⼀个字符出现的个for(auto& e : p){hash1[e-'a']++;}int count = 0;vector<int> ret;for(int left =0,right =0; right < s.size();++right){//入窗hash2[s[right] -'a']++;if(hash2[s[right] -'a'] <= hash1[s[right]-'a']) count++;//判断入窗元素是否为有效数//判断是否出窗if(right - left + 1 > p.size()){if(hash2[s[left] -'a']-- <= hash1[s[left]-'a'])count --;//判断出窗元素是否为有效数。（无论是否为有效数，hash2中对应字符都要减去）left++;}//更新输出结果if(count == p.size())ret.push_back(left);}return ret;}
};

  
  
  
  
  
  

8、串联所有单词的子串(hard)

  题源：链接。

  
  

8.1、滑动窗口

  1）、思路说明
  此题可以视为上一题的升级版，在其基础上披了一层皮。
  题目信息告诉我们，words 中所有字符串长度相同，若把每个单词看成一个一个的字母，问题就变成了找到「字符串中所有的字母异位词」。 无非就是之前处理的对象是单个的字符，这里处理的对象是一个一个的字符串。

  虽然如此，但还是有些细节上的区别:
  1、left、right指针挪动： 移动的步长应该是words中单词的长度。设len = words[0].size()
  2、滑动窗口执行的次数： 因为是视单词为单个字母，这里划分的情况有多种，bar可以是一个组合，同理arf也可以是一个组合。那么滑动窗口的总执行次数应该为len（超过len就回到原先的情况了）

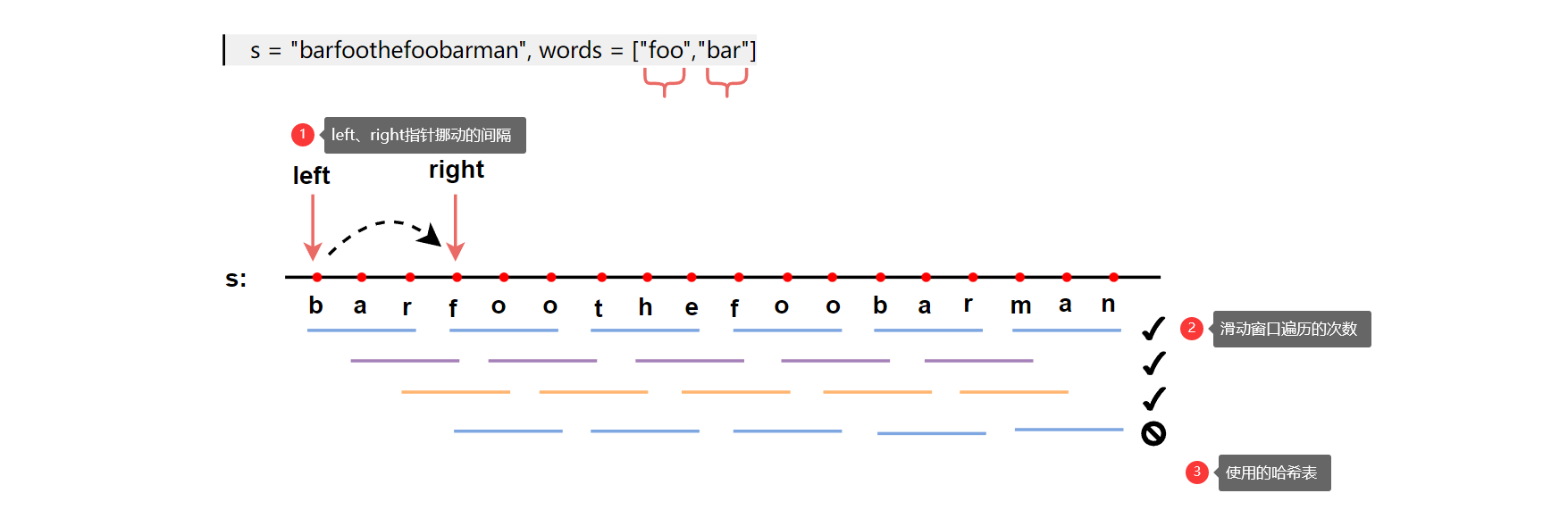
  3、用于记录的哈希表：unordered_map<string,int>，前者指代字符串，后者指代该字符串出现的次数。
  
  
  写法如下：这里直接用维护变量count的写法。

class Solution {
public:vector<int> findSubstring(string s, vector<string>& words) {unordered_map<string,int> hash1;//记录words中的字符串for(auto& e:words) hash1[e]++;int len = words[0].size();//单个单词的长度int size = words.size();//记录words中的字符串个数vector<int> ret;//记录输出结果//滑动窗口要执行的次数for(int i = 0; i < len; ++i ){int count = 0;//用于统计本回合中有效字符串unordered_map<string,int> hash2;//记录s中的字符串for(int left = i, right = i; right + len <= s.size(); right+=len){//入窗：将字符串放入哈希表中，注意维护count(有效字符串)string in = s.substr(right,len);//要入窗的字符串 // string substr (size_t pos = 0, size_t len = npos) const;hash2[in]++;if(hash1.count(in) && hash2[in] <= hash1[in]) count++;//这里使用unordered_map::count是因为[]操作符会有查找+插入两步骤。//判断是否出窗if(right - left + 1 > len * size){//出窗：将字符串挪出哈希表，注意维护count(有效字符串)string out = s.substr(left,len);if(hash1.count(out) && hash2[out] <= hash1[out]) count--;hash2[out]--;left += len;}//更新输出结果if(count == size)ret.push_back(left);}}return ret;}
};

  
  
  
  
  
  

9、最小覆盖子串(hard)

  题源：链接。

  
  

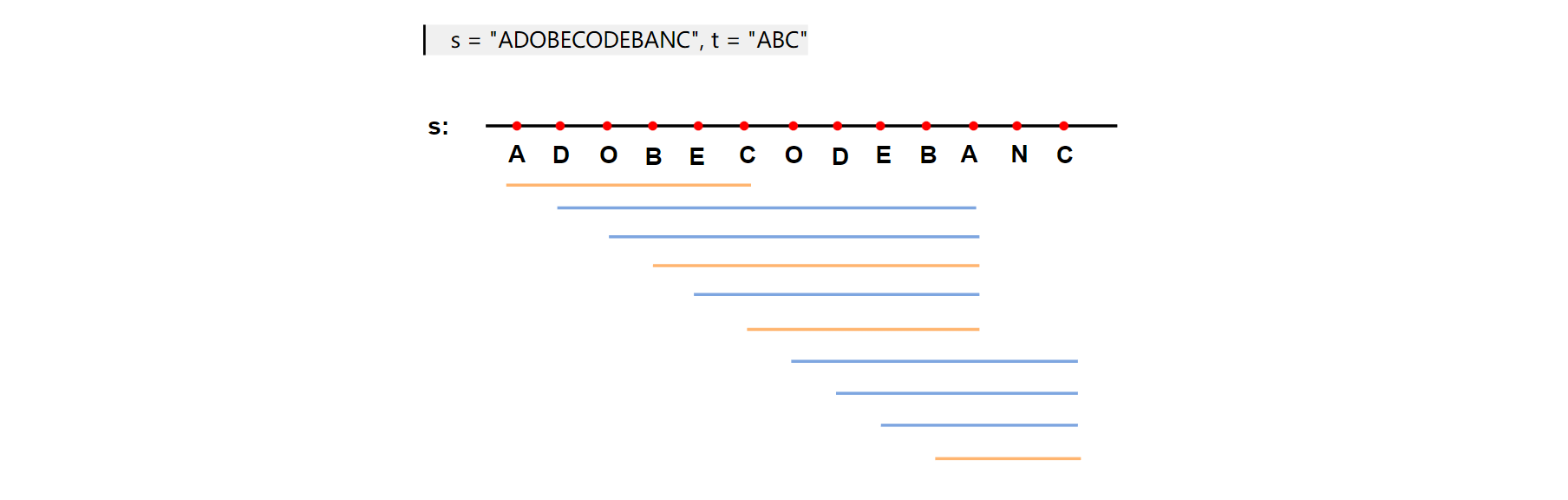
9.1、暴力求解

  暴力解法下， 分别用两个哈希表记录t、滑动窗口中的字符，遍历s找到有效长度，对比获取最小结果。

  
  

9.2、滑动窗口

  在暴力解法上优化，right指针不必回退。left指针向右移动过程中，[left,right]区间内可能出现两种情况：①该区间内的字符串不满足覆盖要求，此时让right++；②该区间的字符串仍旧满足覆盖要求，此时，right指针不动，更新记录本次结果，left++继续下一轮。

  
  如何判断字符覆盖情况：当动态哈希表中包含目标串中所有的字符，并且对应的个数都不小于目标串的哈希表中各个字符的个数，那么当前的窗口就是一种可行的方案。

  1、一种方法是建立两个哈希表，在入窗后，逐一对比两哈希表中的的元素。判断是否满足hash2[ch]>=hash1[ch]。（题目说明子字符串中ch字符数量必须不少于 t 中ch字符数量即可。）
  2、借助count标记有效字符的种类及个数。（这里不能直接统计个数，再用count==t.size()判断，有可能出现字符总数相同，但单字符数目匹配不上的情况）

对某一字符ch:
入窗时：若hash2[ch]== hash1[ch],count++;
出窗时：若hash2[ch]== hash1[ch],count--;
当count==hash1.size()，此时才需要更新窗口。

  

class Solution {
public:string minWindow(string s, string t) {int hash1[128] = {0};int kinds = 0;for (auto& e : t) {if (hash1[e]++ == 0) // 统计字符串 t 中每⼀个字符的频次kinds++;         // 统计 t 中元素种类}int len = INT_MAX; // 用于记录中满足条件的字符串长度int begin = -1;    // 用于记录符合条件的子串起始位置int hash2[128] = {0};int count = 0;for (int left = 0, right = 0; right < s.size(); ++right) {// 入窗+维护countchar in = s[right];if (++hash2[in] == hash1[in])count++;           while (count == kinds) // 判断{if (right - left + 1 < len)// 更新结果{len = right - left + 1;begin = left;}//出窗+维护countchar out = s[left++]; if (hash2[out]-- == hash1[out])count--;}}return begin < 0 ? "" : s.substr(begin, len);}
};

  
  
  
  
  
  
  
  
  
  
  
  

Fin、共勉。