题目列表
3069. 将元素分配到两个数组中 I
3070. 元素和小于等于 k 的子矩阵的数目
3071. 在矩阵上写出字母 Y 所需的最少操作次数
3072. 将元素分配到两个数组中 II
一、将元素分配到两个数组中I
 直接按照题目要求进行模拟即可,代码如下
直接按照题目要求进行模拟即可,代码如下
class Solution {
public:vector<int> resultArray(vector<int>& nums) {int n=nums.size();vector<int>arr1={nums[0]},arr2={nums[1]};for(int i=2;i<n;i++){if(arr1.back()>arr2.back()) arr1.push_back(nums[i]);else arr2.push_back(nums[i]);// (arr1.back() > arr2.back() ? arr1 : arr2).push_back(nums[i]);}arr1.insert(arr1.end(),arr2.begin(),arr2.end());return arr1;}
};二、元素和小于等于k的子矩阵的数目

这题就是求二维前缀和中小于等于k的个数,原理如下

代码如下
class Solution {
public:int countSubmatrices(vector<vector<int>>& grid, int k) {int n=grid.size(),m=grid[0].size(),ans=0;vector<vector<int>>dp(n+1,vector<int>(m+1));for(int i=0;i<n;i++){for(int j=0;j<m;j++){dp[i+1][j+1]=dp[i][j+1]+dp[i+1][j]-dp[i][j]+grid[i][j];if(dp[i+1][j+1]<=k) ans++;}}return ans;}
};三、在矩阵上写出字母Y所需的最小操作次数
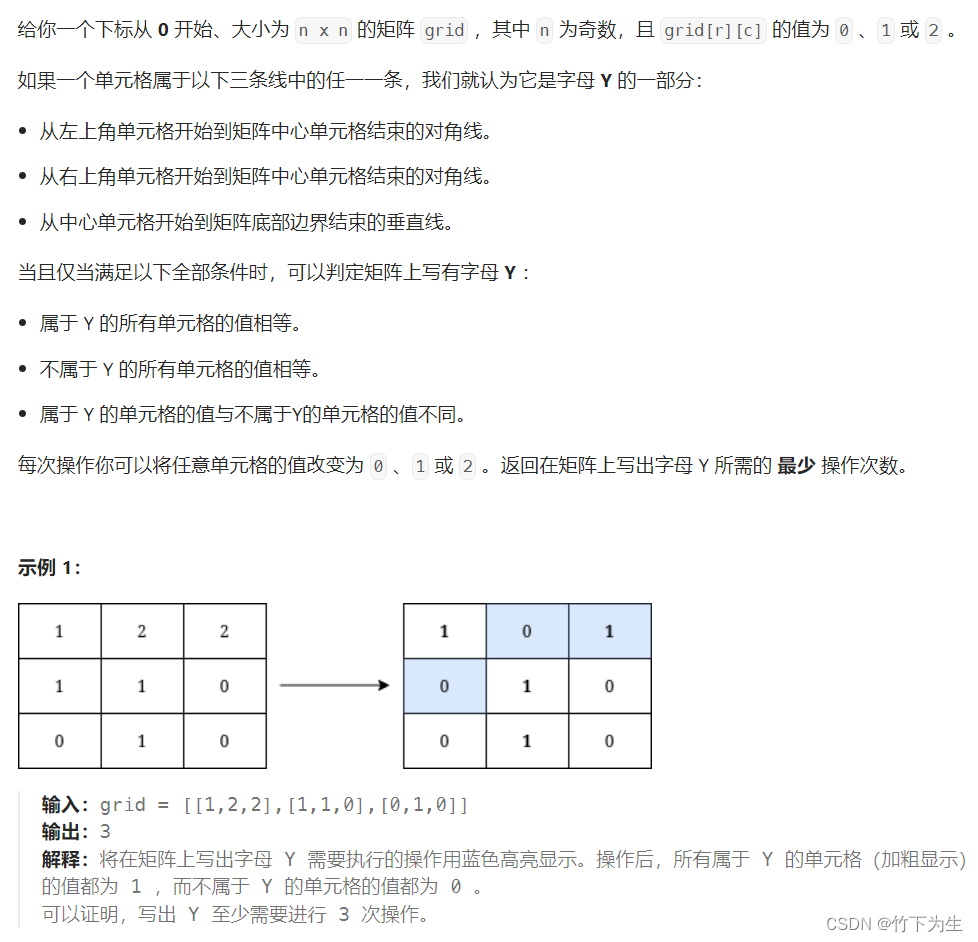
这题的思路其实就是模拟:由于这题的表格中的数字只有0,1,2,所以我们可以直接暴力枚举出所有的可能结果。我们首先要统计一下整个矩阵中0,1,2出现的次数,然后再统计一下组成Y的元素中0,1,2的个数(注意组成Y的元素的下标是有规律的),然后暴力枚举所有的可能结果就行。
代码如下
class Solution {
public:int minimumOperationsToWriteY(vector<vector<int>>& grid) {int n=grid.size(),m=grid[0].size();int sum[3]={0};for(auto& v:grid){for(auto& x:v){sum[x]++;}}int cnt[3]={0};for(int i=0;i<n/2;i++){cnt[grid[i][i]]++;cnt[grid[i][n-1-i]]++;}for(int i=n/2;i<n;i++){cnt[grid[i][n/2]]++;}for(int i=0;i<3;i++) sum[i]-=cnt[i];//在Y之外的数据中0,1,2的个数int ans = n*m;for(int i=0;i<3;i++){for(int j=0;j<3;j++){if(i==j) continue;ans=min(ans,n*m-sum[i]-cnt[j]);}}return ans;}
};扩展:如果grid[i][j]中的数据范围变大了怎么办?(比如变成了0~1e5) 暴力就会超时,如何做?
其实要想让操作次数变少,由于矩阵的大小是确定的,我们只要让保持不变的数据尽可能的多就行,本质就是统计组成Y的元素中出现次数最多和次多的元素个数,和不在Y上的出现次数最多和次多的元素个数,因为我们还要保证组成Y的元素和不在Y上的元素要不一样才行
四、将元素分配到两个数组中II

这题的难点在于greaterCount函数如何去实现,因为我们不仅要查询符合条件的元素个数还要增加元素,这需要用到树状数组(用于解决关于前缀和/前缀最值问题)。

(如果不了解的,可以去看五分钟丝滑动画讲解 | 树状数组_哔哩哔哩_bilibili,讲得简单易懂,这里就不做过多介绍了)
代码如下
class BIT{
private:vector<int> tree;// tree[i]表示<=tmp[i]的元素个数//注意树状数组的第一个元素要从下标1开始
public:BIT(int n):tree(n+1){}//所以要多开一个空间void update(int i,int val=1){while(i<tree.size()){tree[i]+=val;i += (i & -i);}}int pre_sum(int i){int res = 0;while(i>0){res+=tree[i];i&=(i-1);//i -= (i&-i);}return res;}
};
class Solution {
public:vector<int> resultArray(vector<int>& nums) {int n=nums.size();//排序+去重+离散化//作用:将不连续的数字映射到一段连续的数字(即下标)中,并保持它们的大小关系vector<int>tmp(nums);sort(tmp.begin(),tmp.end());tmp.erase(unique(tmp.begin(),tmp.end()),tmp.end());//vector<int>arr1={nums[0]};BIT t1(n);auto idx = upper_bound(tmp.begin(),tmp.end(),nums[0]) - tmp.begin();t1.update(idx);vector<int>arr2={nums[1]};BIT t2(n);idx = upper_bound(tmp.begin(),tmp.end(),nums[1]) - tmp.begin();t2.update(idx);for(int i=2;i<n;i++){idx = upper_bound(tmp.begin(),tmp.end(),nums[i]) - tmp.begin();int cnt1 = arr1.size() - t1.pre_sum(idx);int cnt2 = arr2.size() - t2.pre_sum(idx);if(cnt1>cnt2){arr1.push_back(nums[i]);t1.update(idx);}else if(cnt1<cnt2){arr2.push_back(nums[i]);t2.update(idx);}else{if(arr1.size()>arr2.size()){arr2.push_back(nums[i]);t2.update(idx);}else{arr1.push_back(nums[i]);t1.update(idx);}}}arr1.insert(arr1.end(),arr2.begin(),arr2.end());return arr1;}
};