大模型的训练和推理需要高性能的算力支持。以ChatGPT为例,据估算,在训练方面,1746亿参数的GPT-3模型大约需要375-625台8卡DGX A100服务器训练10天左右,对应A100 GPU数量约3000-5000张。
在推理方面,如果以A100 GPU单卡单字输出需要350ms为基准计算,假设每日访问客户数量高达5,000万人时,按单客户每日发问ChatGPT应用10次,单次需要50字回答,则每日消耗GPU的计算时间将会高达243万个小时,对应的GPU需求数量将超过10万个。
大模型的训练和推理依赖通用GPU
算力即计算能力,具体指硬件对数据收集、传输、计算和存储的能力,算力的大小表明了对数字化信息处理能力的强弱,常用计量单位是FLOPS(Floating-point operations per second),表示每秒浮点运算次数。
当前大模型的训练和推理多采用GPGPU。GPGPU是一种由 GPU 去除图形处理和输出,仅保留科学计算、AI训练和推理功能的GPU。GPU芯片最初用于计算机系统图像显示的运算,但因其相比于擅长横向计算的CPU更擅长于并行计算,在涉及到大量的矩阵或向量计算的AI计算中很有优势,GPGPU应运而生。
在这波ChatGPT浪潮中长期押注AI的英伟达可以说受益最多,ChatGPT、包括各种大模型的训练和推理,基本都采用英伟达的GPU。目前国内多个厂商都在布局GPGPU,包括天数智芯、燧原科技、壁仞科技、登临科技等,不过当前还较少能够应用于大模型。
事实上业界认为,随着模型参数越来越大,GPU在提供算力支持上也存在瓶颈。在GPT-2之前的模型时代,GPU内存还能满足AI大模型的需求,近年来,随着Transformer模型的大规模发展和应用,模型大小每两年平均增长240倍,实际上GPT-3等大模型的参数增长已经超过了GPU内存的增长。传统的设计趋势已经不能适应当前的需求,芯片内部、芯片之间或AI加速器之间的通信成为了AI计算的瓶颈。
存算一体技术如何突破算力瓶颈
而存算一体作为一种新型架构形式受到关注,存算一体将存储和计算有机结合,直接在存储单元中处理数据,避免了在存储单元和计算单元之间频繁转移数据,减少了不必要的数据搬移造成的开销,不仅大幅降低了功耗,还可以利用存储单元进行逻辑计算提高算力,显著提升计算效率。
大模型的训练和部署不仅对算力提出了高要求,对能耗的要求也很高,从这个角度来看,存算一体降低功耗,提升计算效率等特性在大模型方面确实更具优势。
因为独具优势,过去几年已经有众多企业进入到存算一体领域,包括知存科技、千芯科技、苹芯科技、后摩智能、亿铸科技等。各企业的技术方向也有所不同,从介质层面来看,有的采用NOR Flash,有的采用SRAM,也有的采用RRAM。
从目前的情况来看,基于NOR Flash的存算一体产品,在算力上难以做大,应用场景主要是对算力要求不高,对功耗要求高的可穿戴设备等领域;基于SRAM的存算一体算力可以更大些,能够用于自动驾驶领域;而真正能够在算力上实现突破,可以称之为大算力AI芯片的,目前只有亿铸科技主推的基于RRAM的存算一体技术。
在大模型对大算力的需求背景下,亿铸科技近期更是提出了存算一体超异构计算。超异构计算能够把更多的异构计算整合重构,从而各类型处理器间充分地、灵活地进行数据交互而形成的计算。
简单来说,就是结合DSA、GPU、CPU、CIM等多个类型引擎的优势,实现性能的飞跃:DSA负责相对确定的大计算量的工作;GPU负责应用层有一些性能敏感的并且有一定弹性的工作;CPU啥都能干,负责兜底;CIM就是存内计算,超异构和普通异构的主要区别就是加入了CIM,由此可以实现同等算力,更低能耗,同等能耗,更高算力。另外,CIM由于器件的优势,能负担比DSA更大的算力。
亿铸科技创始人、董事长兼CEO熊大鹏博士表示,存算一体超异构计算的好处在于:一是在系统层,能够把整体的效率做到最优;二是在软件层,能够实现跨平台架构统一。
基于存算一体超异构概念,亿铸科技提出了自己的技术畅想:若能把新型忆阻器技术(RRAM)、存算一体架构、芯粒技术(Chiplet)、3D封装等技术结合,将会实现更大的有效算力、放置更多的参数、实现更高的能效比、更好的软件兼容性、从而突破性能瓶颈,抬高AI大算力芯片的发展天花板。
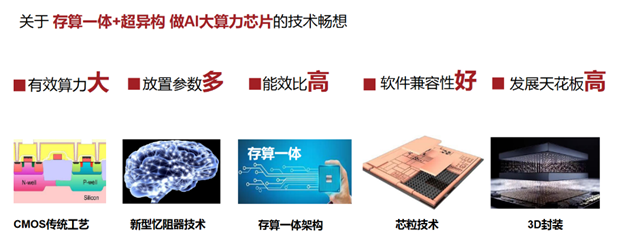
图源:亿铸科技
目前国内已公开的能够实现存算一体AI大算力的芯片公司仅有亿铸科技,其基于RRAM的存算一体AI大算力芯片将在今年回片。
小结
无论是大模型的训练还是部署,对大算力芯片的需求都很大,从目前的情况来看,大模型的训练在很长时间都将要依赖于英伟达的GPU芯片。
而在大模型的推理部署方面,除了GPU,存算一体将是非常合适的选择。未来大模型的部署规模会很大,从前不久英伟达专门推出适合大型语言模型部署的芯片平台也能看出来。据亿铸科技透露,公司规划的产品,在同等功耗下,性能将超越英伟达H100系列的推理芯片。