【leetcode热题】二叉树的后序遍历-编程知识

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

示例 1：

输入：root = [1,null,2,3]
输出：[3,2,1]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

解法一递归

和之前的中序遍历和先序遍历没什么大的改变，只需要改变一下 list.add 的位置。

public List<Integer> postorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();postorderTraversalHelper(root, list);return list;
}private void postorderTraversalHelper(TreeNode root, List<Integer> list) {if (root == null) {return;}postorderTraversalHelper(root.left, list);postorderTraversalHelper(root.right, list);list.add(root.val);
}

解法二栈

主要就是用栈要模拟递归的过程，区别于之前 94 题中序遍历和 144 题先序遍历，后序遍历的非递归形式会相对难一些。

原因就是，当遍历完某个根节点的左子树，回到根节点的时候，对于中序遍历和先序遍历可以把当前根节点从栈里弹出，然后转到右子树。举个例子，

     1/ \2   3/ \4   5

当遍历完 2,4,5 的时候，回到 1 之后我们就可以把 1 弹出，然后通过 1 到达右子树继续遍历。

而对于后序遍历，当我们到达 1 的时候并不能立刻把 1 弹出，因为遍历完右子树，我们还需要将这个根节点加入到 list 中。

所以我们就需要判断是从左子树到的根节点，还是右子树到的根节点。

如果是从左子树到的根节点，此时应该转到右子树。如果是从右子树到的根节点，那么就可以把当前节点弹出，并且加入到 list 中。

当然，如果是从左子树到的根节点，此时如果根节点的右子树为 null，此时也可以把当前节点弹出，并且加入到 list 中。

基于上边的思想，可以写出一些不同的代码。

1. 思想一

可以先看一下中序遍历的实现。

public List<Integer> inorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;while (cur != null || !stack.isEmpty()) {//节点不为空一直压栈while (cur != null) {stack.push(cur);cur = cur.left; //考虑左子树}//节点为空，就出栈cur = stack.pop();//当前值加入ans.add(cur.val);//考虑右子树cur = cur.right;}return ans;
}

这里后序遍历的话，和中序遍历有些像。

开始的话，也是不停的往左子树走，然后直到为 null 。不同之处是，之前直接把节点 pop 并且加入到 list 中，然后直接转到右子树。

这里的话，我们应该把节点 peek 出来，然后判断一下当前根节点的右子树是否为空或者是否是从右子树回到的根节点。

判断是否是从右子树回到的根节点，这里我用了一个 set ，当从左子树到根节点的时候，我把根节点加入到 set 中，之后我们就可以判断当前节点在不在 set 中，如果在的话就表明当前是第二次回来，也就意味着是从右子树到的根节点。

public List<Integer> postorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();Set<TreeNode> set = new HashSet<>();TreeNode cur = root;while (cur != null || !stack.isEmpty()) {while (cur != null && !set.contains(cur)) {stack.push(cur);cur = cur.left;}cur = stack.peek();//右子树为空或者第二次来到这里if (cur.right == null || set.contains(cur)) {list.add(cur.val);set.add(cur);stack.pop();//将当前节点弹出if (stack.isEmpty()) {return list;}//转到右子树，这种情况对应于右子树为空的情况cur = stack.peek();cur = cur.right;//从左子树过来，加到 set 中，转到右子树} else {set.add(cur);cur = cur.right;}}return list;
}

上边的代码把一些情况其实做了合并，并不是很好理解，下边分享一下 solution 里的一些简洁的解法。

2. 思想二

上边的解法在判断当前是从左子树到的根节点还是右子树到的根节点用了 set ，这里还有一个更直接的方法，通过记录上一次遍历的节点。

如果当前节点的右节点和上一次遍历的节点相同，那就表明当前是从右节点过来的了。

public List<Integer> postorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;TreeNode last = null;while (cur != null || !stack.isEmpty()) {if (cur != null) {stack.push(cur);cur = cur.left;} else {TreeNode temp = stack.peek();//是否变到右子树if (temp.right != null && temp.right != last) {cur = temp.right;} else {list.add(temp.val);last = temp;stack.pop();}}}return list;
}

3. 思想三

在这里看到另一种想法，还是基于上边分析的入口点，不过解决方案真的是太优雅了。

先看一下 144 题前序遍历的代码。

我们还可以将左右子树分别压栈，然后每次从栈里取元素。需要注意的是，因为我们应该先访问左子树，而栈的话是先进后出，所以我们压栈先压右子树。

public List<Integer> preorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();if (root == null) {return list;}Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()) {TreeNode cur = stack.pop();if (cur == null) {continue;}list.add(cur.val);stack.push(cur.right);stack.push(cur.left);}return list;
}

后序遍历遇到的问题就是到根节点的时候不能直接 pop ，因为后边还需要回来。

上边的作者，提出只需要把每个节点 push 两次，然后判断当前 pop 节点和栈顶节点是否相同。

相同的话，就意味着是从左子树到的根节点。

不同的话，就意味着是从右子树到的根节点，此时就可以把节点加入到 list 中。

public List<Integer> postorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();if (root == null) {return list;}Stack<TreeNode> stack = new Stack<>();stack.push(root);stack.push(root);while (!stack.isEmpty()) {TreeNode cur = stack.pop();if (cur == null) {continue;}if (!stack.isEmpty() && cur == stack.peek()) {stack.push(cur.right);stack.push(cur.right);stack.push(cur.left);stack.push(cur.left);} else {list.add(cur.val);}}return list;
}

解法三转换问题

首先我们知道前序遍历的非递归形式会比后序遍历好理解些，那么我们能实现后序遍历 -> 前序遍历的转换吗？

后序遍历的顺序是 左 -> 右 -> 根。

前序遍历的顺序是 根 -> 左 -> 右，左右其实是等价的，所以我们也可以轻松的写出 根 -> 右 -> 左 的代码。

然后把 根 -> 右 -> 左 逆序，就是 左 -> 右 -> 根，也就是后序遍历了。

让我们改一下之前 144 题先序遍历的代码。

改之前的代码。

public List<Integer> preorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;while (cur != null || !stack.isEmpty()) {if (cur != null) {list.add(cur.val);stack.push(cur);cur = cur.left; //考虑左子树}else {//节点为空，就出栈cur = stack.pop();//考虑右子树cur = cur.right;}}return list;
}

然后我们只需要把上边的 left 改成 right，right 改成 left 就可以了。最后倒置即可。

public List<Integer> postorderTraversal2(TreeNode root) {List<Integer> list = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;while (cur != null || !stack.isEmpty()) {if (cur != null) {list.add(cur.val);stack.push(cur);cur = cur.right; // 考虑左子树} else {// 节点为空，就出栈cur = stack.pop();// 考虑右子树cur = cur.left;}}Collections.reverse(list);return list;
}

同样的，之前先序遍历的 Morris Traversal ，不需要额外空间的解法。

public List<Integer> preorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();TreeNode cur = root;while (cur != null) {//情况 1if (cur.left == null) {list.add(cur.val);cur = cur.right;} else {//找左子树最右边的节点TreeNode pre = cur.left;while (pre.right != null && pre.right != cur) {pre = pre.right;}//情况 2.1if (pre.right == null) {list.add(cur.val);pre.right = cur;cur = cur.left;}//情况 2.2if (pre.right == cur) {pre.right = null; //这里可以恢复为 nullcur = cur.right;}}}return list;
}

同样的处理，把上边的 left 改成 right，right 改成 left 就可以了。最后倒置即可。

public List<Integer> postorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();TreeNode cur = root;while (cur != null) {if (cur.right == null) {list.add(cur.val);cur = cur.left;} else {TreeNode pre = cur.right;while (pre.left != null && pre.left != cur) {pre = pre.left;}if (pre.left == null) {list.add(cur.val);pre.left = cur;cur = cur.right;}if (pre.left == cur) {pre.left = null; // 这里可以恢复为 nullcur = cur.left;}}}Collections.reverse(list);return list;
}

上边的话由于我们用的是 ArrayList ，所以倒置的话其实是比较麻烦的，可能需要更多的时间或空间。

所以我们可以用 LinkedList ，这样倒置链表就只需要遍历一遍，也不需要额外的空间了。

更近一步，我们在调用 list.add 的时候，其实可以直接 list.addFirst ，每次都插入到链表头，这样做的话，最后也不需要逆转链表了。

解法四 Morris Traversal

上边已经成功改写 Morris Traversal 了，但是是一种取巧的方式，通过变形的前序遍历做的。同学介绍了另一种写法，这里也分享下。

94 题中序遍历中对 Morris 遍历有详细的介绍，我先贴过来。

我们知道，左子树最后遍历的节点一定是一个叶子节点，它的左右孩子都是 null，我们把它右孩子指向当前根节点，这样的话我们就不需要额外空间了。这样做，遍历完当前左子树，就可以回到根节点了。

当然如果当前根节点左子树为空，那么我们只需要保存根节点的值，然后考虑右子树即可。

所以总体思想就是：记当前遍历的节点为 cur。

1、cur.left 为 null，保存 cur 的值，更新 cur = cur.right

2、cur.left 不为 null，找到 cur.left 这颗子树最右边的节点记做 last

2.1 last.right 为 null，那么将 last.right = cur，更新 cur = cur.left

2.2 last.right 不为 null，说明之前已经访问过，第二次来到这里，表明当前子树遍历完成，保存 cur 的值，更新 cur = cur.right

结合图示：

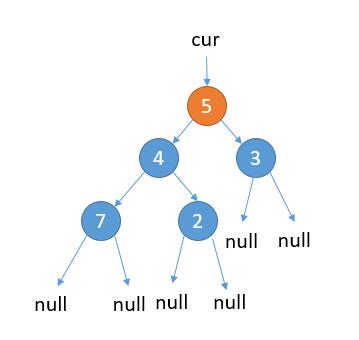
如上图，cur 指向根节点。当前属于 2.1 的情况，cur.left 不为 null，cur 的左子树最右边的节点的右孩子为 null，那么我们把最右边的节点的右孩子指向 cur。

接着，更新 cur = cur.left。

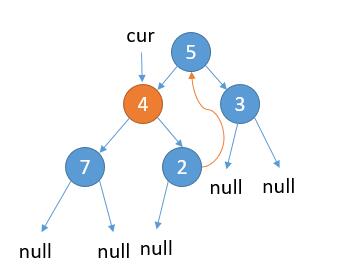
如上图，当前属于 2.1 的情况，cur.left 不为 null，cur 的左子树最右边的节点的右孩子为 null，那么我们把最右边的节点的右孩子指向 cur。

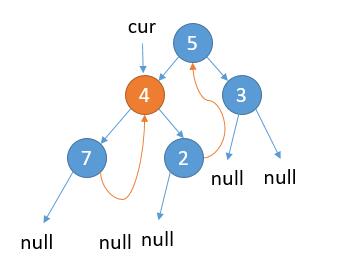
更新 cur = cur.left。

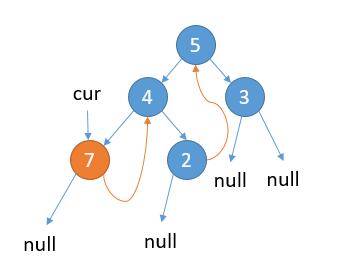
如上图，当前属于情况 1，cur.left 为 null，保存 cur 的值，更新 cur = cur.right。

如上图，当前属于 2.2 的情况，cur.left 不为 null，cur 的左子树最右边的节点的右孩子已经指向 cur，保存 cur 的值，更新 cur = cur.right。

如上图，当前属于情况 1，cur.left 为 null，保存 cur 的值，更新 cur = cur.right。

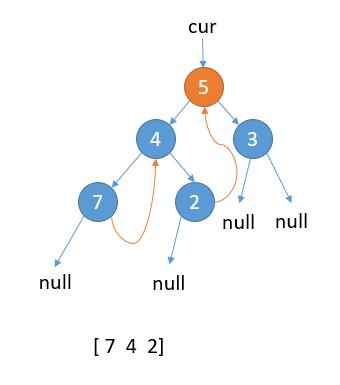
如上图，当前属于 2.2 的情况，cur.left 不为 null，cur 的左子树最右边的节点的右孩子已经指向 cur，保存 cur 的值，更新 cur = cur.right。

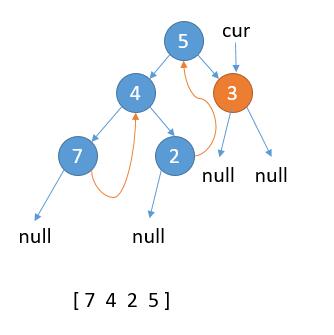
当前属于情况 1，cur.left 为 null，保存 cur 的值，更新 cur = cur.right。

cur 指向 null，结束遍历。

根据这个关系，写代码

记当前遍历的节点为 cur。

1、cur.left 为 null，保存 cur 的值，更新 cur = cur.right

2、cur.left 不为 null，找到 cur.left 这颗子树最右边的节点记做 last

2.1 last.right 为 null，那么将 last.right = cur，更新 cur = cur.left

2.2 last.right 不为 null，说明之前已经访问过，第二次来到这里，表明当前子树遍历完成，保存 cur 的值，更新 cur = cur.right

public List<Integer> inorderTraversal(TreeNode root) {List<Integer> ans = new ArrayList<>();TreeNode cur = root;while (cur != null) {//情况 1if (cur.left == null) {ans.add(cur.val);cur = cur.right;} else {//找左子树最右边的节点TreeNode pre = cur.left;while (pre.right != null && pre.right != cur) {pre = pre.right;}//情况 2.1if (pre.right == null) {pre.right = cur;cur = cur.left;}//情况 2.2if (pre.right == cur) {pre.right = null; //这里可以恢复为 nullans.add(cur.val);cur = cur.right;}}}return ans;
}

根据上边的关系，我们会发现除了叶子节点只访问一次，其他节点都会访问两次，结合下图。

当第二次访问某个节点的时候，我们只需要将它的左节点，以及左节点的右节点，左节点的右节点的右节点... 逆序添加到 list 中即可。比如上边的例子。

上边的遍历顺序其实就是按照深度优先的方式。

先访问 15, 7, 3, 1 然后往回走
3 第二次访问，将它的左节点逆序加入到 list 中
list = [1]继续访问 2, 然后往回走
7 第二次访问，将它的左节点，左节点的右节点逆序加入到 list 中
list = [1 2 3]继续访问 6 4, 然后往回走
6 第二次访问, 将它的左节点逆序加入到 list 中
list = [1 2 3 4]继续访问 5, 然后往回走
15 第二次访问, 将它的左节点, 左节点的右节点, 左节点的右节点的右节点逆序加入到 list 中
list = [1 2 3 4 5 6 7]然后访问 14 10 8, 然后往回走
10 第二次访问，将它的左节点逆序加入到 list 中
list = [1 2 3 4 5 6 7 8]继续访问 9, 然后往回走
14 第二次访问，将它的左节点，左节点的右节点逆序加入到 list 中
list = [1 2 3 4 5 6 7 8 9 10]继续访问 13 11, 然后往回走
13 第二次访问, 将它的左节点逆序加入到 list 中
list = [1 2 3 4 5 6 7 8 9 10 11]继续遍历 12，结束遍历然后单独把根节点，以及根节点的右节点，右节点的右节点，右节点的右节点的右节点逆序加入到 list 中
list = [1 2 3 4 5 6 7 8 9 10 11 12 13 14 15]得到 list 就刚好是后序遍历

如下图，问题就转换成了 9 组单链表的逆序问题。

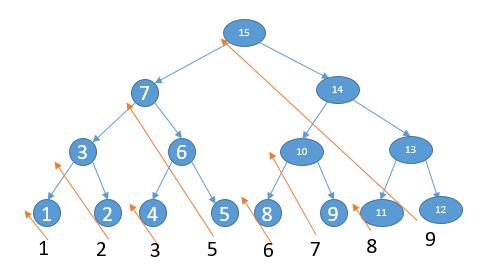
当遇到第二次访问的节点，我们将单链表逆序，然后加入到 list 并且还原即可。单链表逆序已经在第 2 题讨论过了，直接拿过来用，只需要把 node.next 改为 node.right 。

public List<Integer> postorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();TreeNode cur = root;while (cur != null) {// 情况 1if (cur.left == null) {cur = cur.right;} else {// 找左子树最右边的节点TreeNode pre = cur.left;while (pre.right != null && pre.right != cur) {pre = pre.right;}// 情况 2.1if (pre.right == null) {pre.right = cur;cur = cur.left;}// 情况 2.2,第二次遍历节点if (pre.right == cur) {pre.right = null; // 这里可以恢复为 null//逆序TreeNode head = reversList(cur.left);//加入到 list 中，并且把逆序还原reversList(head, list);cur = cur.right;}}}TreeNode head = reversList(root);reversList(head, list);return list;
}private TreeNode reversList(TreeNode head) {if (head == null) {return null;}TreeNode tail = head;head = head.right;tail.right = null;while (head != null) {TreeNode temp = head.right;head.right = tail;tail = head;head = temp;}return tail;
}private TreeNode reversList(TreeNode head, List<Integer> list) {if (head == null) {return null;}TreeNode tail = head;head = head.right;list.add(tail.val);tail.right = null;while (head != null) {TreeNode temp = head.right;head.right = tail;tail = head;list.add(tail.val);head = temp;}return tail;
}