宽度优先搜索算法（BFS）-编程知识

宽度优先搜索算法（BFS）是什么？

宽度优先搜索算法（BFS）（也称为广度优先搜索）主要运用于树、图和矩阵（这三种可以都归类在图中），用于在图中从起始顶点开始逐层地向外探索，直到找到目标顶点为止。

在本篇文章中，我们主要讨论其在树中的运用

树的宽度优先搜索

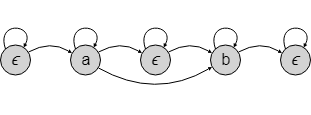
树的宽度优先搜索即树的层序遍历 ：逐层访问树的节点，并按照层级顺序输出节点的值。从树的根节点开始，逐层向下遍历，先访问当前层的所有节点，然后再访问下一层的节点，依次类推直到遍历完整棵树

其过程如下图所示：

如何实现树的层序遍历呢？

我们在遍历每一层节点时，都是从左向右依次遍历的，即先遍历上一层节点中的第一个节点的孩子节点，即优先遍历前面的节点，此时，满足 “先进先出”，因此，我们可以使用队列来帮助我们完成层序遍历

具体步骤如下：

1. 先将根节点放入队列中

2. 从队列中出队一个节点，并将该节点的所有孩子节点（如果有）依次放入队列中

3. 继续取出节点，指导队列为空

4. 当队列为空时，遍历完成

接下来，我们通过一些练习来进一步体会和掌握BFS

相关练习

练习1：N叉树的层序遍历

题目链接：

429. N 叉树的层序遍历 - 力扣（LeetCode）

题目描述：

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

示例 1：

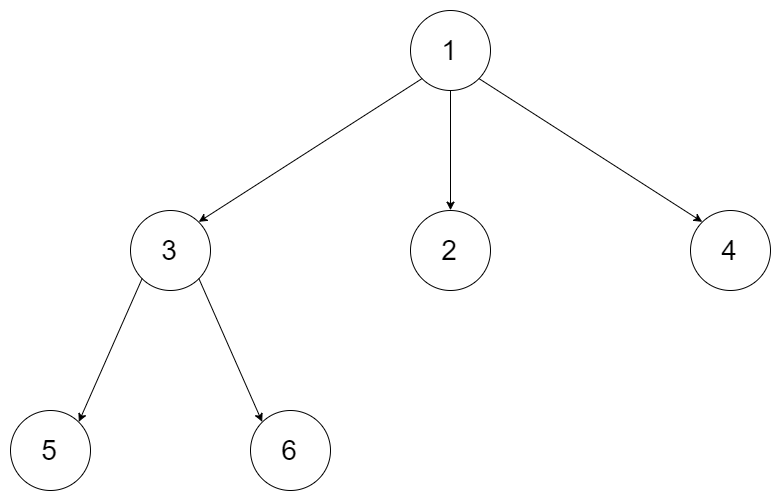
输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

示例 2：

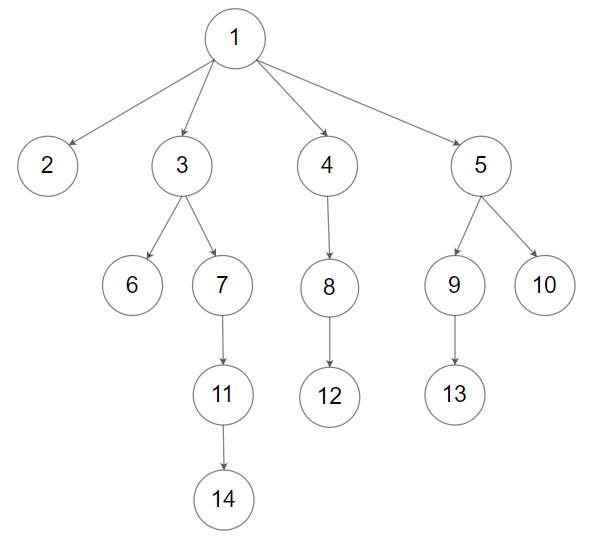
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

提示：

树的高度不会超过 1000
树的节点总数在 [0, 10^4] 之间

思路分析：

本题要求我们返回N叉树节点值的层序遍历，且以 List<List<Integer>>类型的结果返回，即每一层使用一个列表来存储本层的所有节点的值，然后将这些列表放到一个列表中返回

在这里，我们可以使用队列来帮助我们进行层序遍历，但在将节点出队时，也会将其孩子节点放入队列中，那么，我们如何区分每一层的节点呢？

我们可以使用一个变量 count 在节点出队之前，记录队列当前节点个数（即这一层节点个数），然后再将这 count 个节点依次出队列，将其节点值放入列表中，同时将其孩子节点放入队列中

具体步骤：

1. 先判断树是否为空，不为空将根节点放入队列中

2. 记录当前队列中包含的节点个数count

3. 将count个节点依次出队列，将其节点值放入一个临时列表中，同时将其孩子节点放入队列中

4. 遍历完count个节点后，临时列表中就存放了这一层所有节点的值，然后再将临时列表放入结果列表中

5. 继续遍历，直到队列为空

6. 返回结果

代码实现：

class Solution {public List<List<Integer>> levelOrder(Node root) {List<List<Integer>> ret = new ArrayList<>();Node cur = root;Queue<Node> queue = new ArrayDeque<>();//先将根节点放入队列中if(cur == null) return ret;queue.add(cur);int count = 0;while (!queue.isEmpty()){//先记录当前队列中节点个数count = queue.size();List<Integer> tmp = new ArrayList<>();//使用临时表存储这一层节点的值for (int i = 0; i < count; i++) {cur = queue.poll();//将队头元素出队tmp.add(cur.val);for (Node child: cur.children) {//将队头元素的孩子节点放入队列中queue.add(child);}}ret.add(tmp);//将临时表放入ret中}return ret;}
}

练习2：二叉树的锯齿形层序遍历

题目链接：

103. 二叉树的锯齿形层序遍历 - 力扣（LeetCode）

题目描述：

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-100 <= Node.val <= 100

思路分析：

本题要求我们返回二叉树的锯齿形层序遍历，

什么是锯齿形层序遍历？

先从左向右，再从右向左地对每一层节点进行遍历

以示例1为例：

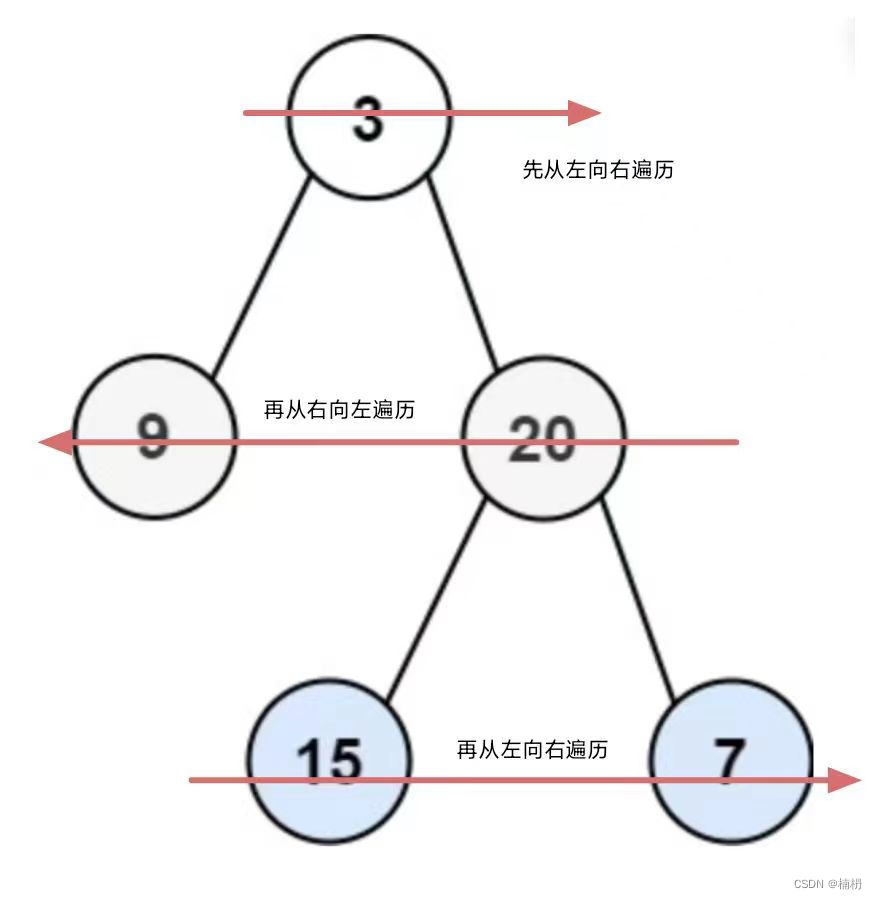
即当前层数为奇数时，从左向右遍历；当前层数为偶数时，从右向左遍历

因此，本题的解题思路与练习1类似，唯一不同的是：在偶数层时需要将所有节点的值进行逆序，我们可以使用一个int类型的变量（或boolean类型的变量）来标记这一层的节点是否需要逆序

代码实现：

class Solution {public List<List<Integer>> zigzagLevelOrder(TreeNode root) {List<List<Integer>> ret = new ArrayList<>();Queue<TreeNode> queue = new ArrayDeque<>();int flag = 1;//标识是否需要逆序TreeNode cur = root;//先将根节点放入队列中if(cur == null) return ret;queue.add(cur);int count = 0;while(!queue.isEmpty()){//先记录当前队列节点个数count = queue.size();//依次出队列List<Integer> tmp = new ArrayList<>();for(int i = 0; i < count; i++){cur = queue.poll();tmp.add(cur.val);//将其孩子节点入队列if(cur.left != null) queue.add(cur.left);if(cur.right != null) queue.add(cur.right);}//判断是否需要逆序if(flag == -1){Collections.reverse(tmp);}ret.add(tmp);flag = -flag;}return ret;}
}

练习3：在每个树行中找最大值

题目链接：

LCR 044. 在每个树行中找最大值 - 力扣（LeetCode）

题目描述：

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

示例1：

输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]
解释:1/ \3   2/ \   \  5   3   9

示例2：

输入: root = [1,2,3]
输出: [1,3]
解释:1/ \2   3

示例3：

输入: root = [1]
输出: [1]

示例4：

输入: root = [1,null,2]
输出: [1,2]
解释:      1 \2

示例5：

输入: root = []
输出: []

提示：

二叉树的节点个数的范围是 [0,104]
-231 <= Node.val <= 231 - 1

思路分析：

题目要求我们找到二叉树中每一层中的最大值，因此，我们只需要进行层序遍历，并在每一层中寻找最大值即可

代码实现：

class Solution {public List<Integer> largestValues(TreeNode root) {List<Integer> ret = new ArrayList<>();TreeNode cur = root;Queue<TreeNode> queue = new ArrayDeque<>();//先将根节点放入if(cur == null) return ret;queue.add(cur);int count = 0;while(!queue.isEmpty()){//先计算队列中有多少个元素count = queue.size();//将元素依次出队列int max = Integer.MIN_VALUE;for(int i = 0; i < count; i++){cur = queue.poll();if(max < cur.val){//寻找这一层的最大值max = cur.val;}//将其孩子节点放入队列中if(cur.left != null) queue.add(cur.left);if(cur.right != null) queue.add(cur.right);}ret.add(max);//将这一层的最大值添加到ret中}return ret;}
}

练习4：二叉树的最大宽度

题目链接：

662. 二叉树最大宽度 - 力扣（LeetCode）

题目描述：

给你一棵二叉树的根节点 root ，返回树的 最大宽度 。

树的 最大宽度 是所有层中最大的宽度。

每一层的宽度被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

题目数据保证答案将会在 32 位 带符号整数范围内。

示例 1：

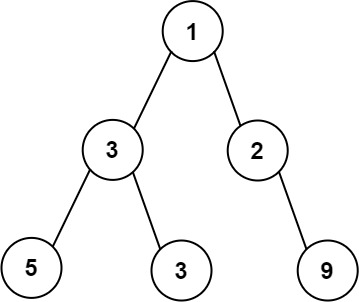
输入：root = [1,3,2,5,3,null,9]
输出：4
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。

示例 2：

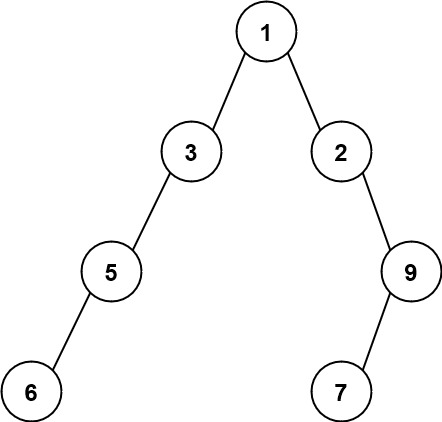
输入：root = [1,3,2,5,null,null,9,6,null,7]
输出：7
解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。

示例 3：

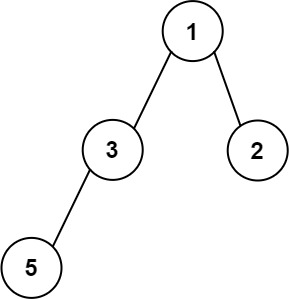
输入：root = [1,3,2,5]
输出：2
解释：最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。

提示：

树中节点的数目范围是 [1, 3000]
-100 <= Node.val <= 100

思路分析：

题目要求我们返回二叉树的最大宽度，需要注意的是：这里的宽度不是指这一层有多少个节点，而是指这一层最左端的非空节点left和最右端的非空节点right之间的长度，left和right之间为空或不存在的节点也需计入长度

我们以示例2为例：

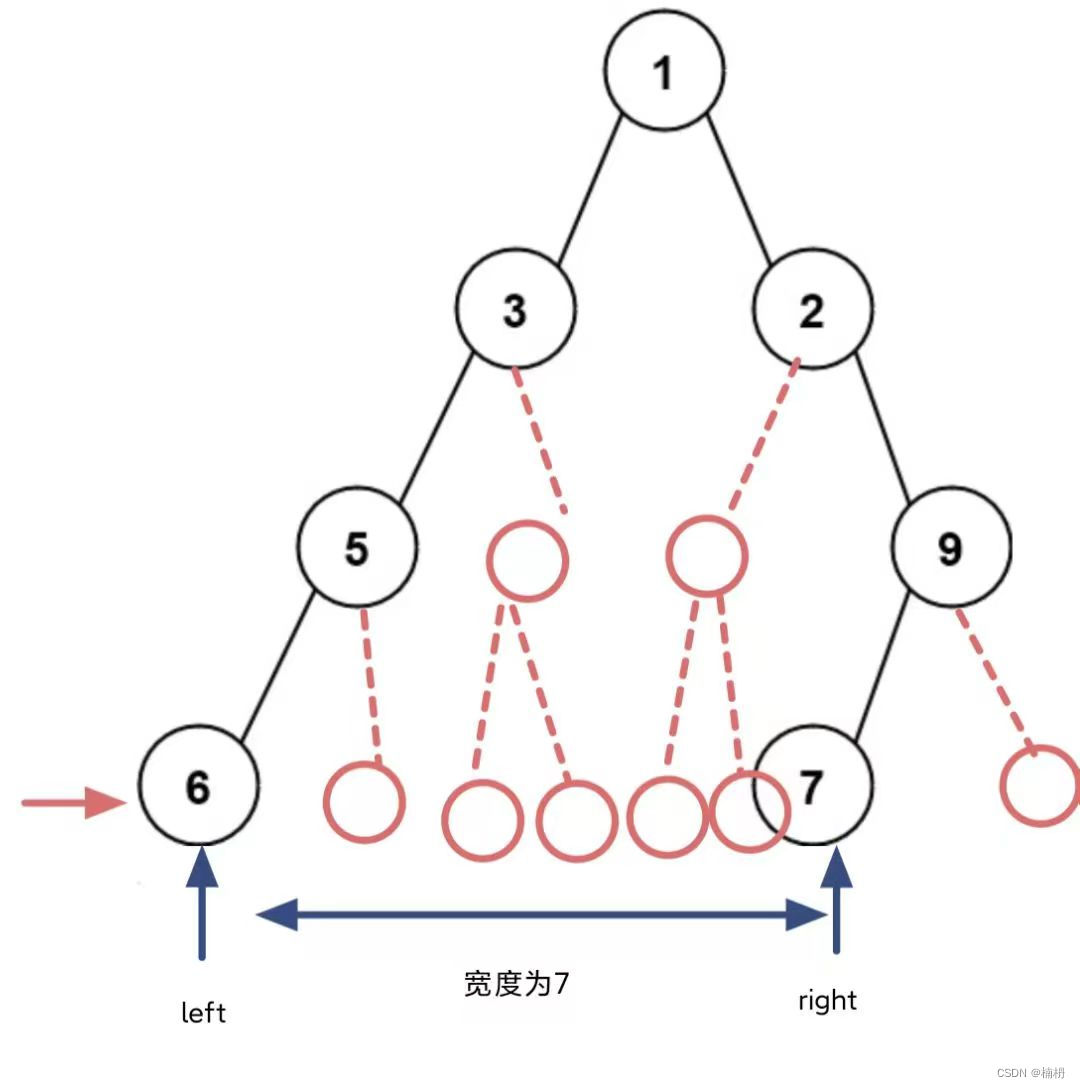
left和right之间的节点及其延伸到这一层的null节点都要计入，因此，我们首先可以想到：可以添加这些空节点，即若当前节点的右孩子为空，则将null入队列；若当前节点为null，则将null null两个节点入队列，这样，我们就补齐了这一层两端点之间的节点，因此可以直接使用 count 变量记录这一层的宽度，但是，虽然树中节点的数目范围为 1 - 3000，但若出现极端情况，即：

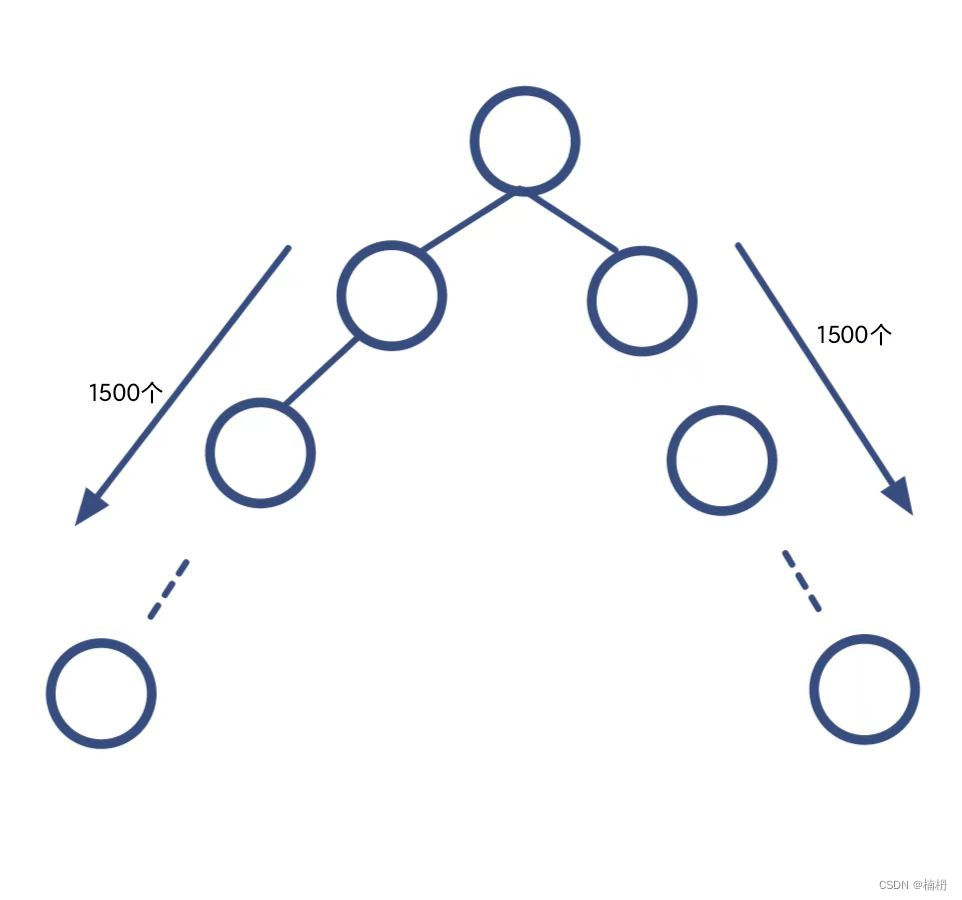
此时，需要补充的空节点数量非常多，超出时间限制，因此，该方法不能解决本题

本层宽度 = 最左端的非空节点left和最右端的非空节点right之间的长度，因此，我们可以直接寻找最左端非空节点left的位置和最右端非空节点right的位置，然后就可以直接求出这一层的宽度

如何找到最左端非空节点left的位置和最右端非空节点right的位置?

我们对节点进行编号，从1开始（即根节点为1），这样当前节点cur的编号为index，则其左孩子为2*index，右孩子为2*index + 1，通过编号，我们就能很容易的找到每一个节点，此时， 每一层的宽度 = 最右侧非空节点right的编号 - 最左侧非空节点left的编号 + 1，在这里，我们使用 Pair(配对) 来关联当前节点和其编号

具体步骤：

1. 将根节点及其编号1放入队列中，此时最大宽度为1

2. 先记录当前队列中元素个数count

3. 将count个元素依次出队列，记录第一个节点的编号和最后一个节点的编号，遍历过程中，将当前节点的孩子节点和编号放入队列中

4. 计算该层宽度 right - left + 1，并更新最大宽度

5. 继续遍历，直达队列为空

代码实现：

class Solution {public int widthOfBinaryTree(TreeNode root) {TreeNode cur = root;Queue<Pair<TreeNode, Integer>> queue = new ArrayDeque<>();queue.add(new Pair<TreeNode, Integer>(root, 1));//将根节点添加到队列中int ret = 1;//最大宽度int count = 0;while(!queue.isEmpty()){count = queue.size();int left = 0, right = 0;//记录最左端和最右端非空节点的编号for(int i = 0; i < count; i++){Pair<TreeNode, Integer> pair = queue.poll();int index = pair.getValue();if(i == 0) left = index;//第一个非空节点if(i == count - 1) right = index;//最后一个非空节点cur = pair.getKey();if(cur.left != null) queue.add(new Pair<TreeNode, Integer>(cur.left, index*2));if(cur.right != null) queue.add(new Pair<TreeNode, Integer>(cur.right, index*2 + 1));}ret = Math.max(ret, right - left + 1);//更新最大宽度}return ret;}
}