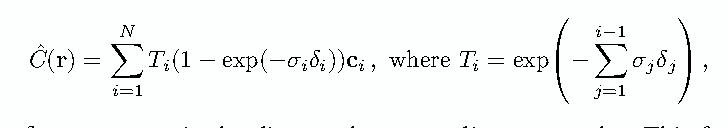参考视频:https://www.youtube.com/watch?v=HfJpQCBTqZs&ab_channel=Vision%26GraphicsSeminaratMIT
NeRF模型的输入输出:
输入:
- (x, y, z): 一个三维空间坐标,代表场景中的一个位置点
- (θ, φ): 视线方向,θ表示与y轴的夹角,φ表示与x轴的夹角,用两个角度可以唯一确定一条射线的方向
输出: NeRF模型的输出是一个由4个量组成的向量(r, g, b, σ):
- (r, g, b): RGB三个通道的颜色值,范围在[0, 1]
- σ: 密度值(density),范围在[0, +∞)
具体来说:
- (r, g, b)表示在输入的(x, y, z)位置处,沿(θ, φ)方向看去,这个位置出射的RGB颜色值
- σ表示在输入位置(x, y, z)处的体渲染密度(volumetric density)。体渲染密度可以理解为空间中的不透明度或者云雾的浓度
NeRF是通过体渲染积分(volumetric rendering integral)计算出最终的颜色C:
C = ∫(x,y,z)∈R r(x, y, z, θ, φ)σ(x, y, z, θ, φ)exp(-∫0tσ(r(s))ds)dt
其中r是射线方程,t是沿射线的距离。可以看出,最终的颜色C是网络预测的(r, g, b)与密度σ,以及体渲染积分的结合。

![]()
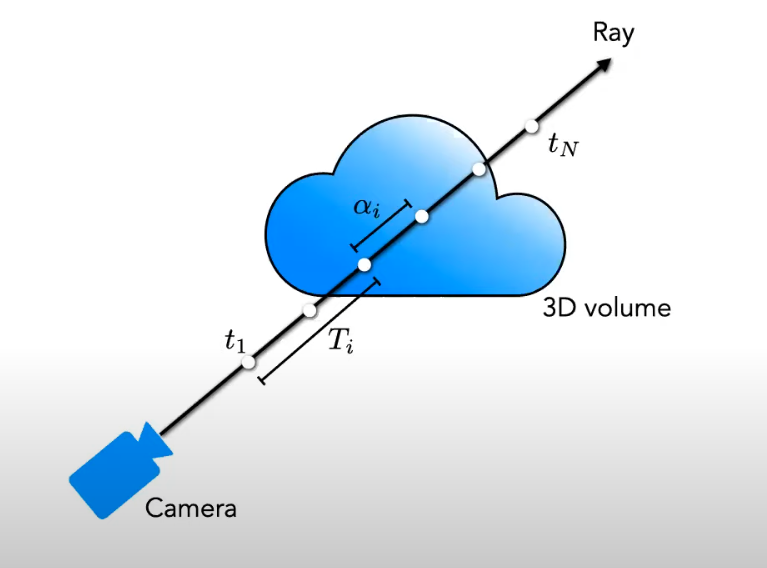
σ(x) 是点密度,可以解释为射线终止于位置 x 处的无穷小粒子的微分概率。
![]()

不透明度 ( \alpha_i )
( T_i ) 代表的是从光线起点到第 ( i ) 点之间的透射率 也就是这段路径上光线没有被吸收的量。因此,( T_i ) 实际上是一个衰减因子,它确保了只有未被前面的介质吸收的光线才能贡献到最终的颜色。

最终颜色 ( C ) 和不透明度 ( \alpha_i ) 成正比是因为不透明度决定了每一段路径对最终颜色的贡献。不透明度高的区域意味着光线在该区域被吸收得更多,因此这一区域对光线的颜色贡献也更大。