目录
一.引言:神经网络与偏微分方程
二.如何基于神经网络求解偏微分方程
1.简要概述
2.基于神经网络求解偏微分方程的三大方向
2.1数据驱动
基于CNN
基于其他网络
2.2物理约束
PINN
基于 PINN
可测量标签数据
2.3物理驱动(纯物理约束)
全连接神经网路(FC-NN)
CNN 求解偏微分方程
三.基于神经网络偏微分方程求解的新突破
一.引言:神经网络与偏微分方程
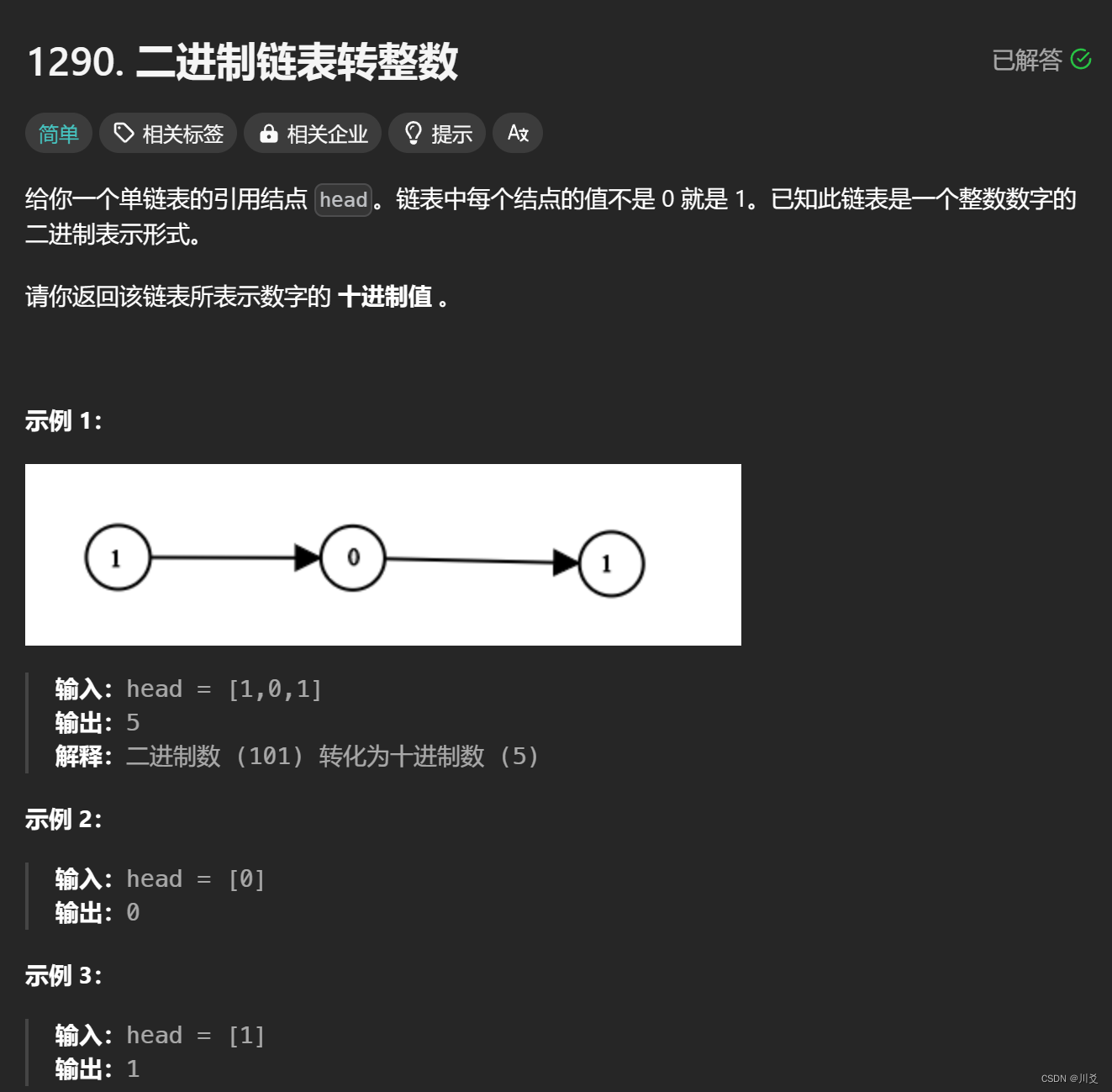
基于神经网络可以求解偏微分方程。通常情况下,神经网络将数据从一个有限维空间(例如,图像的像素值)映射或转换为另一个有限维空间(例如,将图像分类的数字,例如1代表猫,2代表狗)。求解偏微分方程的神经网络则是从无穷大的空间映射到无穷大的空间。
偏微分方程的用处和复杂性相伴而生,例如,想要观察空气在飞机机翼附近的流动二维透视图,建模人员想知道流体在空间中任何一点(也称为流场)以及在不同时间的速度和压力的话,就需要用到偏微分方程。考虑到能量、质量和动量守恒定律,特定的偏微分方程,即Navier-Stokes方程可以对这种流体流动进行建模。
在这些情况下,建模者会转向数值方法,将偏微分方程转换为一组易于处理的代数方程,假定这些方程可保持很小的空间和时间增量。在超级计算机上,用数值方式解决复杂的偏微分方程可能要花费数月的时间。如果初始条件或边界条件或所研究系统的几何形状(例如机翼设计)发生了变化,就必须重新开始求解。使用的增量越小(如研究人员所说,网格越细),模型的精度越高,数值求解所需的时间就越长。
神经网络更擅长拟合这样一个黑盒的未知函数,输入是一个向量,而输出是另一个向量。如果存在将一组输入向量映射到一组输出向量的函数,则可以训练网络以学习该映射,两个有限维空间之间的任何函数都可以通过神经网络近似。
2016年,研究人员研究了如何将通常用于图像识别的深度神经网络用于解决偏微分方程。首先,研究人员生成了用于训练网络的数据:一个数值求解器计算了流过xy且大小和方向不同的基本形状(三角形,四边形等)的简单对象上流动的流体的速度场。
二.如何基于神经网络求解偏微分方程
1.简要概述
使用神经网络来解决偏微分方程的基本思想是将偏微分方程转化为一个可学习的模型,然后使用神经网络来学习这个模型。
下面是一个简单的步骤概述:
- 1. 定义问题:首先需要定义要解决的偏微分方程问题。这可能包括选择适当的坐标系、定义边界条件和初始条件等。
- 2. 离散化:将连续的偏微分方程转化为离散的形式。这可以通过将空间和时间域划分为网格来实现。
- 3. 构建神经网络:构建一个神经网络来逼近离散化后的偏微分方程。神经网络的输入可以是网格点上的初始条件和边界条件,输出可以是下一个时间步长的网格点上的解。
- 4. 训练神经网络:使用训练数据来训练神经网络。训练数据可以是通过数值方法求解偏微分方程得到的结果。
- 5. 预测:使用训练好的神经网络来预测新的初始条件和边界条件下的解。
需要注意的是,神经网络方法并不是一种精确的解析方法,而是一种数值方法。因此,其预测结果可能存在一定的误差。此外,神经网络的训练需要大量的数据和计算资源,因此在实际应用中需要考虑到这些因素。
总的来说,使用神经网络来解决偏微分方程是一种有前途的方法,但需要仔细选择模型和训练数据,以确保预测结果的准确性和可靠性。
2.基于神经网络求解偏微分方程的三大方向
2.1数据驱动
基于CNN
1.PDE-Net 2.0
是一种基于深度学习的偏微分方程(PDE)发现方法。它通过结合数值近似和符号神经网络,从观察到的动态数据中发现(时变的)PDE。这种方法具有很高的灵活性和表达能力,可以学习到微分算子和底层PDE模型的非线性响应函数。
2.基于卷积的三维非稳态偏微分方程模型求解方法
基于卷积的三维非稳态偏微分方程模型求解方法是由华侨大学计算机科学与技术学院的金镇上提出的。该方法以偏微分方程的差分格式为基础构造卷积迭代格式并提取卷积核,通过卷积核扫描数值解图像的方式逼近偏微分方程的解。该方法直接在数值解图像上进行卷积迭代,从而替代了传统数值方法求解离散线性方程组的过程。数值算例表明,卷积迭代方法在 GPU 上求解大规模问题的效率优于传统 ADI 算法等。
基于其他网络
1.神经网络作为一种函数逼近器及其在解决微分方程中的应用
神经网络作为一种函数逼近器在解决微分方程中有广泛的应用。下面是一些基本的概念和应用:
- 1. 函数逼近:神经网络可以通过调整网络的权重来逼近任意函数。它们可以学习输入和输出之间的映射关系,从而实现对复杂函数的逼近。
- 2. 微分方程求解:对于常微分方程(ODE)或偏微分方程(PDE),可以将其转化为函数逼近问题。通过使用神经网络来逼近微分方程的解函数,可以实现对微分方程的数值求解。
- 3. 数值积分:对于积分问题,可以使用神经网络来逼近被积函数,然后通过数值积分方法计算积分结果。
- 4. 边值问题:对于边值问题,例如求解ODE的初值问题或PDE的边界条件问题,可以使用神经网络来逼近解函数,并结合数值方法求解。
- 5. 模型预测和控制:神经网络可以用于构建微分方程的模型,从而进行预测和控制。通过学习输入和输出之间的关系,可以预测系统的未来状态,并实现对系统的控制。
2.使用深度学习解决高维偏微分方程
使用深度学习解决高维偏微分方程是一个活跃的研究领域,它结合了深度学习的强大建模能力和偏微分方程的数学描述来解决复杂的物理问题。
以下是一些基本概念和方法:
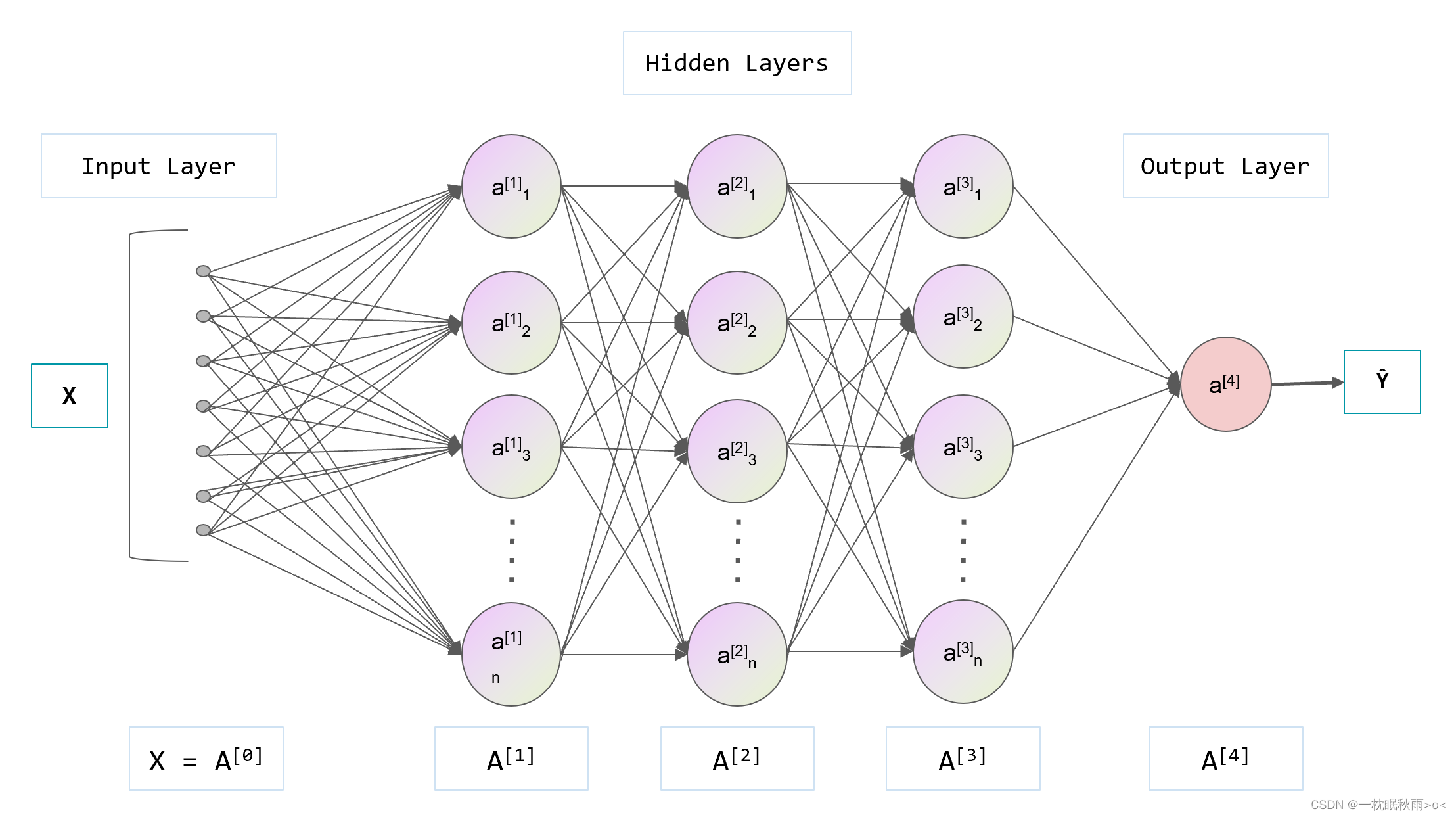
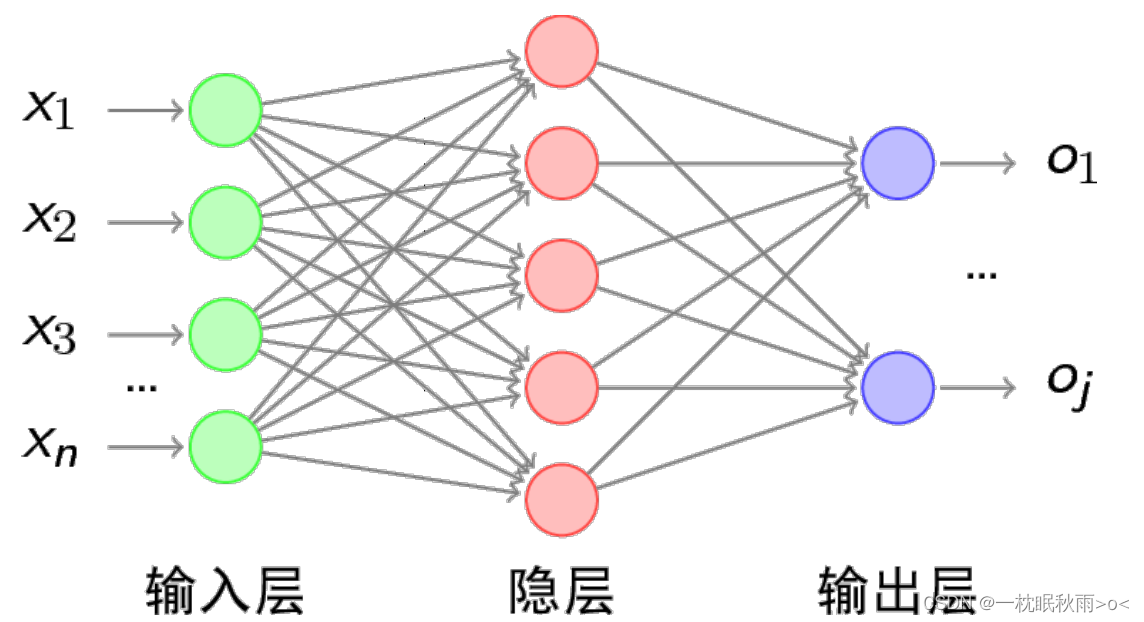
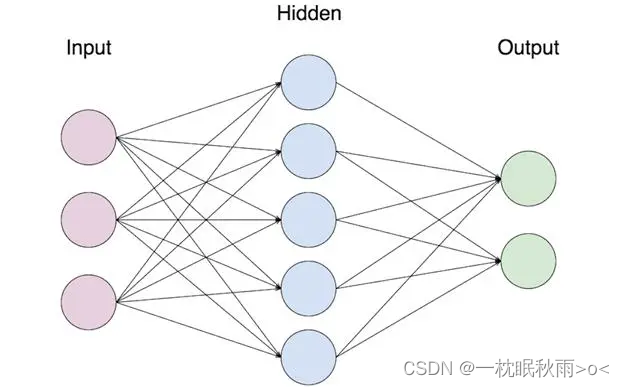
- 1. 深度神经网络:深度神经网络(DNN)是一种常见的深度学习模型,由多个神经元层组成,可以学习输入数据和输出之间的复杂映射关系。
- 2. 物理模型:偏微分方程描述了物理系统中的动态行为,例如流体力学、电磁学、量子力学等。
- 3. 数据驱动方法:通过使用大量的数值模拟或实验数据来训练深度学习模型,使其能够学习到物理系统的行为和特征。
- 4. 模型预测:训练好的深度学习模型可以用于预测物理系统的未来状态或响应,例如流场的演化、物体的运动等。
- 5. 结合数值方法:深度学习可以与传统的数值方法相结合,以提高求解的精度和效率。
3.基于深度学习的高维抛物型偏微分方程和向后随机微分方程的数值方法
基于深度学习的高维抛物型偏微分方程和向后随机微分方程的数值方法是一种利用深度学习技术来求解高维抛物型偏微分方程和向后随机微分方程的数值方法。这种方法的基本思想是将高维问题映射到低维空间,然后使用深度学习模型来学习低维空间中的映射关系。
以下是一些基本步骤:
- 1. 空间降维:通过使用特征提取或其他降维技术,将高维问题映射到低维空间。
- 2. 深度学习模型:构建深度学习模型,例如神经网络或循环神经网络,以学习低维空间中的映射关系。
- 3. 数值求解:使用训练好的深度学习模型来近似求解高维抛物型偏微分方程或向后随机微分方程。
- 4. 模型评估和优化:通过与传统数值方法或真实解进行比较,评估深度学习模型的准确性,并进行必要的优化。
这种方法的优点是可以利用深度学习的强大建模能力来处理高维问题,并且可以自动学习问题的特征和模式。然而,需要注意的是,深度学习模型的准确性和泛化能力可能受到数据和模型选择的影响,因此需要进行适当的评估和验证。
2.2物理约束
PINN
1.物理学启发的深度学习
物理学启发的深度学习是一种将物理学原理和概念应用于深度学习的方法。它旨在利用物理学中的对称、守恒定律和优化原理等来设计更强大、更高效的深度学习模型。
以下是一些物理学启发的深度学习的例子:
- 1. 物理系統建模:利用物理学中的牛顿力学、热力学等原理来构建深度学习模型,以模拟物理系統的行为和特征。
- 2. 对称约束:利用物理学中的对称原理,如旋转对称、平移对称等,来约束深度学习模型的结构,提高模型的泛化能力和效率。
- 3. 守恒定律:利用物理学中的能量守恒、动量守恒等定律来设计深度学习模型,以确保模型在学习过程中保持某些物理量的守恒。
- 4. 优化方法:借鉴物理学中的优化方法,如牛顿法、梯度下降法等,来优化深度学习模型的参数。
- 5. 物理信息神经网络:结合物理学中的先验知识和约束,设计具有物理意义的神经网络结构和损失函数,以提高模型的准确性和可解释性。
物理学启发的深度学习旨在将物理学的原理和方法与深度学习相结合,以解决复杂的科学和工程问题,并推动深度学习在物理学领域的应用。
基于 PINN
1.Richardson-Richards方程的单调约束物理神经网络
Richardson-Richards方程的物理信息神经网络(PINN)是一种基于深度学习的方法,用于求解Richardson-Richards方程。PINN是一种利用物理信息来约束神经网络的方法,它通过将物理规律转化为神经网络的约束条件,使得神经网络能够更好地模拟物理系统的行为。
Richardson-Richards方程是一种描述油藏驱替过程的偏微分方程,它在石油工程中有着广泛的应用。通过使用PINN来求解Richardson-Richards方程,可以提高计算效率和精度,并且可以更好地处理复杂的油藏模型。
可测量标签数据
1.基于理论指导的神经网络对地下流的深度学习
2.3物理驱动(纯物理约束)
全连接神经网路(FC-NN)
1.通过重要性采样对物理知识神经网络进行高效训练
通过重要性采样对物理知识神经网络进行高效训练是一种基于概率推理的训练方法。重要性采样是一种在概率分布中进行采样的技术,它可以根据样本的重要性来调整采样概率,从而更有效地利用有限的样本。
在物理知识神经网络的训练中,重要性采样可以用于优化训练过程,提高模型的泛化能力和准确性。具体来说,可以通过以下步骤实现高效训练:
- 1. 定义目标概率分布:根据物理问题的特点,定义目标概率分布,即物理量的真实分布。
- 2. 设计重要性采样策略:根据目标概率分布,设计合适的重要性采样策略,以更有针对性地获取具有代表性的样本。
- 3. 训练神经网络:使用重要性采样策略采集到的样本训练物理知识神经网络,以学习物理量之间的关系和规律。
- 4. 模型评估和优化:通过与真实数据或其他基准方法进行比较,评估训练得到的物理知识神经网络的性能,并进行必要的优化。
通过重要性采样对物理知识神经网络进行高效训练可以提高训练效率和模型的泛化能力,但需要根据具体问题进行合理的设计和调整。
CNN 求解偏微分方程
用于求解不规则域上的参数化稳定状态PDE的物理信息几何自适应卷积神经网络
提出了一种基于卷积神经网络(CNN)的物理知识神经网络(PINN),用于高效求解不规则域上的参数化偏微分方程(PDEs),无需任何标记数据。通过引入椭圆坐标映射,实现了不规则物理域和规则参考域之间的坐标转换,从而利用了强大的经典CNN主干网络。数值实验表明,该方法在效率和准确性上优于目前最先进的基于全连接神经网络的PINN,可用于解决具有参数化边界条件、可变几何形状和空间变化源场的稳态PDE。
三.基于神经网络偏微分方程求解的新突破
https://new.qq.com/rain/a/20240229A02ZMH00
近年来,基于神经网络的偏微分方程求解器在各领域均得到了广泛关注。其中,量子变分蒙特卡洛方法(NNVMC)在量子化学领域异军突起,对于一系列问题的解决展现出超越传统方法的精确度 [1, 2, 3, 4]。北京大学与字节跳动研究部门 ByteDance Research 联合开发的计算框架 Forward Laplacian 创新地利用 Laplace 算子前向传播计算,为 NNVMC 领域提供了十倍的加速,从而大幅降低计算成本,达成该领域多项 State of the Art,同时也助力该领域向更多的科学难题发起冲击。该工作以《A computational framework for neural network-based variational Monte Carlo with Forward Laplacian》为题的论文已发表于国际顶级期刊《Nature Machine Intelligence》,相关代码已开源。
代码地址:
https://github.com/bytedance/LapNet
https://github.com/YWolfeee/lapjax
该项工作一提出即受到相关研究人员的密切关注,围绕该工作已有多个开源项目实现,编程框架 JAX 也计划将该项工作吸收其中。
该项工作由北京大学智能学院王立威课题组、物理学院陈基课题组联合字节跳动研究部门 ByteDance Research 一同开发完成,作者中有多位北京大学博士生在 ByteDance Research 实习。
背景简介
基于神经网络的量子变分蒙特卡洛方法(NNVMC)已成为量子化学 - 从头计算领域中一项前沿技术。它具备精度高、适用范围广等优点。但它的阿克琉斯之踵在于过高的计算成本,这也限制了该方法在实际化学问题中的应用。
作者提出了一套全新的计算框架 "Forward Laplacian",利用 Laplace 算子的前向传播,显著提升了 NNVMC 方法的计算效率,为人工智能在微观量子问题中的应用打开了新的大门。
方法介绍
Forward Laplacian 框架
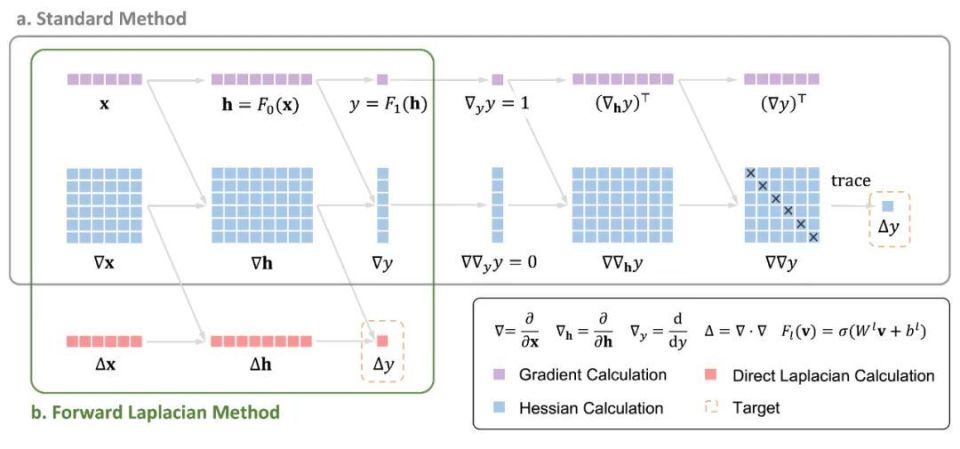
在 NNVMC 方法中,神经网络的目标函数是微观体系的能量,包括动能与势能两项。其中动能项涉及对神经网络的拉普拉斯算子的计算,这也是 NNVMC 中耗时最长的计算瓶颈。现有的自动微分框架在计算拉普拉斯算子时,需要先计算黑塞矩阵,再求得拉普拉斯项(即黑塞矩阵的迹)。而作者所提出的计算框架 "Forward Laplacian" 则通过一次前向传播直接求得拉普拉斯项,避免了黑塞矩阵的计算,从而削减了整体计算的规模,实现了显著加速。
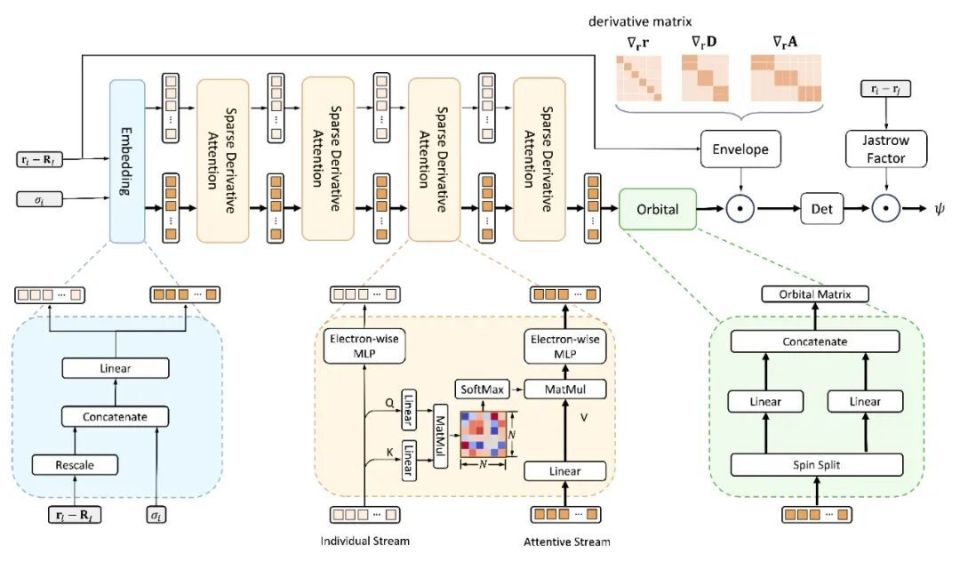
LapNet 网络
除了有效削减计算图规模之外,Forward Laplacian 框架的另一大特点是能有效利用神经网络梯度计算中的稀疏性,提出神经网络结构 LapNet。LapNet 通过增加神经网络中的稀疏性,在精度无损的同时,显著提升了网络计算的效率。
计算结果
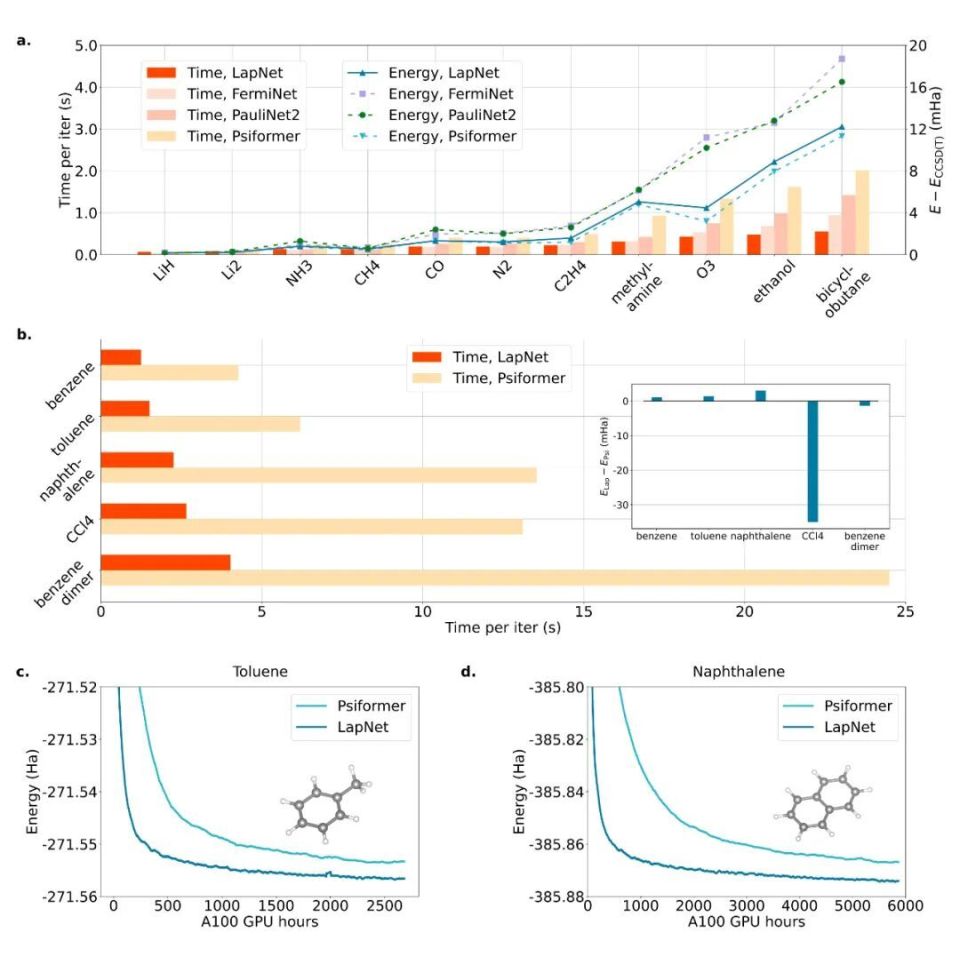
绝对能量
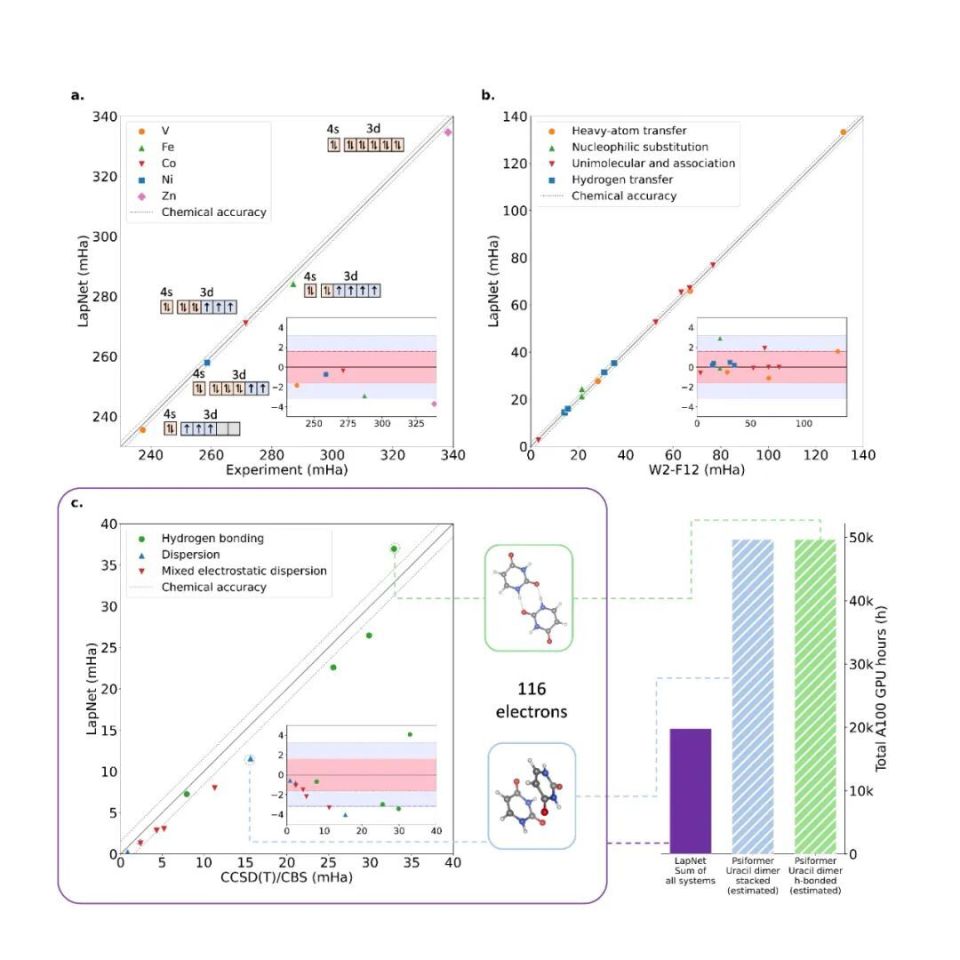
作者首先就方法的效率及精度同当前 NNVMC 领域有代表性的几项工作进行了比较。从绝对能量的计算结果而言,作者提出的 LapNet 在 Forward Laplacian 框架下的效率高于参考工作数倍,精度上也与 SOTA 保持一致。此外,如果在相同计算资源(即相同 GPU hour)的情况下比较,LapNet 的计算结果可以显著优于之前的 SOTA。
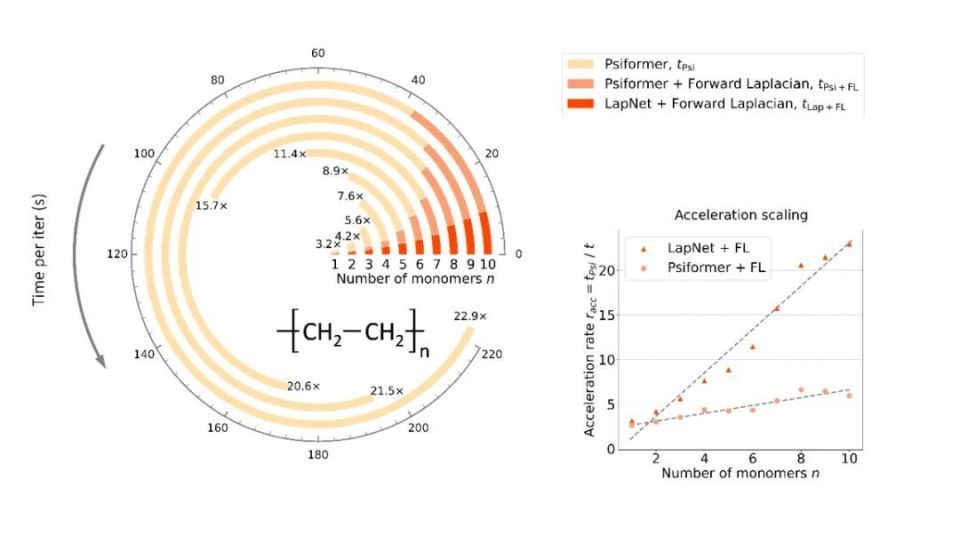
加速标度
为了更明确地研究作者所提出方法相比于之前 SOTA 的加速标度,作者在不同大小的链式聚乙烯体系上进行了测试,结果可以很明显地看到 Forward Laplacian 工作带来的 O (n) 加速。此处 n 为目标分子中的电子数目。
相对能量
在物理、化学研究中,相对能量相较于绝对能量具有更明确的物理意义。作者也在一系列的体系上进行了测试,均取得了理想结果。







![基础 | JVM - [指令 性能监控]](https://img-blog.csdnimg.cn/4c8e35e825dc4a329492fa73af951161.png)