【编程】典型题目:寻找数组第K大数(四种方法对比)
文章目录
- 【编程】典型题目:寻找数组第K大数(四种方法对比)
- 1. 题目
- 2. 题解
- 2.1 方法一:全局排序(粗暴)
- 2.2 方法二:局部排序(略粗暴)
- 2.3 方法三:优先队列(合理)
- 2.4 方法四:快速排序(完美)
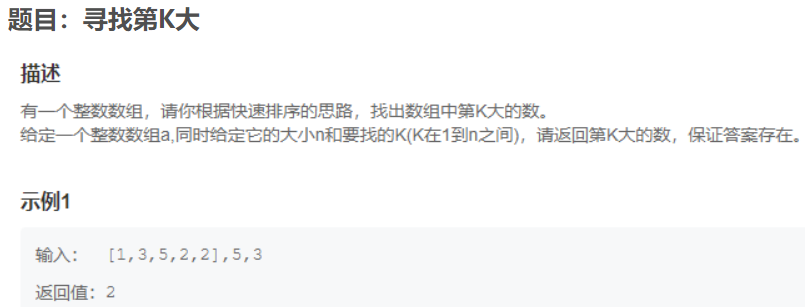
1. 题目
2. 题解
2.1 方法一:全局排序(粗暴)
使用C++中内置函数sort进行全局排序,再取第K大值:
class Solution {
public:int findKth(vector<int> a, int n, int K) {sort(a.begin(), a.end());return a[n-K];}
};
- 复杂度:O(n log n)
2.2 方法二:局部排序(略粗暴)
使用冒泡排序的思想,每次将最大的值放在数组尾部,直到第K个:
class Solution {
public:int findKth(vector<int> a, int n, int K) {for(int i=0; i<K; ++i){for(int j=0; j<n-i-1; ++j){if(a[j]>a[j+1]){int temp = a[j];a[j] = a[j+1];a[j+1] = temp;}}}return a[n-K];}
};
- 复杂度:O(nk)
2.3 方法三:优先队列(合理)
小根堆,维护一个大小为k的小根堆:
class Solution {
public:int findKth(vector<int> a, int n, int K) {priority_queue <int, deque<int>, greater<int>> nums; //队首最小,从小到大排序for(int i=0; i<n; ++i){if(i<K){nums.push(a[i]);}else{if(a[i]>nums.top()){nums.pop();nums.push(a[i]);}}}return nums.top();}
};
- 复杂度:O(n logk)
2.4 方法四:快速排序(完美)
快排思想:通过一趟排序将待排序元素分成独立的两部分,其中一部分记录的元素均比另一部分记录的元素要小,则可分别对这两部分记录继续进行排序,直到整个序列有序为止。具体做法如下:
- 首先选取基准元素base(首元素,中间元素,最后元素,随机元素等等)。
- 以基准元素为基准,将小于基准元素的元素放在前面,大于基准元素的放在后面。
- 然后以基准元素为界限,分为两组数据。
- 两组元素重复1、2和3步骤,直至比较排序完成。
快排的最坏运行时间为O(n^2),平均运行时间为O(nlogn)。由于跳跃式交换比较,故不稳定(稳定是指:值一样的原始顺序保持不变)。
针对这道题,递归直到 base 右边有k-1个数,停止即可。
class Solution {
public:vector<int> quickSort(vector<int>&nums, int start, int end, int K){if (start >= end) return nums;int base = nums[start];int i = start;int j = end;while (i < j){while (i < j && nums[j] >= base) j--; //从右往左,寻找比base小的数swap(nums[i], nums[j]);while (i < j && nums[i] <= base) i++;swap(nums[i], nums[j]);}if(nums.size()-i<K) //如果base右边的数超过K个,则第K大数肯定在base右边,此时就不需要对base左边的进行排序quickSort(nums, start, i - 1, K);quickSort(nums, i + 1, end, K);return nums;}int findKth(vector<int> a, int n, int K) {quickSort(a, 0, n-1, K);return a[n-K];}
};
- 时间复杂度:最坏O(n log n),最好O(n)