论文题目：Cooperative Differential Evolution With an Attention-Based Prediction Strategy for Dynamic Multiobjective Optimization

基于注意力预测策略的动态多目标优化合作差分进化论（Xiao-Fang Liu , Member, IEEE, Jun Zhang, Fellow, IEEE, and Jun Wang , Life Fellow, IEEE）IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS: SYSTEMS, VOL. 53, NO. 12, DECEMBER 2023

刚开始学习多目标优化算法，不作商业用途，如果有不正确的地方请指正！

个人总结：

背景及相关工作

差分进化算法回顾

DE算法使用一个种群通过多代来寻找最优解。记种群规模为S，优化函数为f ( X )。种群中的每个个体i都有一个位置Xi = [ Xi , 1 , ... , Xi , d , ... , Xi , D]，其中d为维度指标，D为决策空间的维度。每一代每个个体执行变异和交叉算子来更新自己

提出的算法

提出的CDE - AP算法使用多个种群来近似动态PF。CDE - AP由3部分组成：

1 )用于优化的协同DE算法；

2 )环境变化检测流程；

3 )一种应对环境变化的AP策略。

A. Cooperative Differential Evolution(合作差分进化)

为了近似PF的各个部分，采用多个种群来优化多个目标。每个种群只优化一个称为种群目标的目标函数。例如，第j个种群Pj只优化第j个目标函数fj ( X )。

外部存档A收集来自所有种群的非支配解用于信息共享。存档中的解在不同的目标上表现良好，可以协助所有种群向PF收敛。

在每一代中，每个种群都使用新的基于融合的变异策略来更新个体。

Fusion-Based Mutation Strategy(基于融合的变异策略)

传统的变异策略选择同一种群中的个体构建差分向量进行更新.在这种情况下,个体的其他目标不能得到充分的优化导致整体向PF的收敛效果较差.所以提出了基于融合的变异算子:

其中j是种群指数,i是个体指数,Ajmbest是根据种群目标Fj(x)从档案A中排名前1/M位的个体中随机选择的解.Ar1和Ar2是从档案中随机选择的两个不同的解. 具体突变策略如图所示

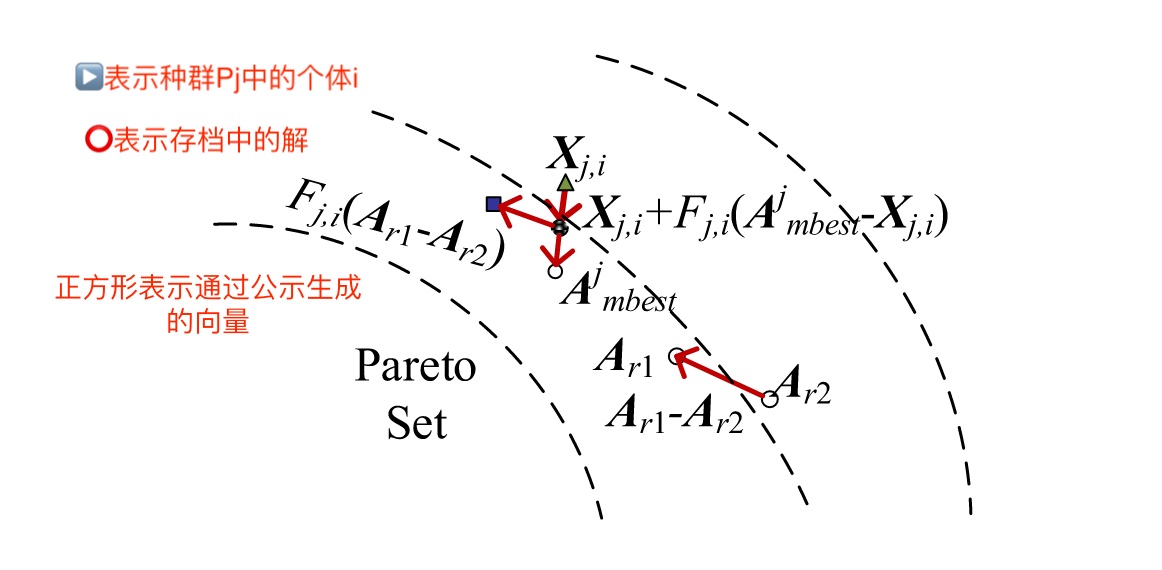
所提出的突变策略使用一个在第 j 个目标函数上表现良好的非支配解决方案和另外两个非主导解决方案来扰乱个体。这样，其他种群的优化信息就可以整合到当前种群中。个体能够向目标PF区域移动，并在fj（X）上具有良好的值。  变异的概率是根据差分进化的参数机制生成的.

Expanding Procedure(扩展程序

由于每个种群都旨在找到具有自身种群目标的最佳解决方案，因此种群倾向于聚集在 PF 极端。为了将种群覆盖的区域扩展到整个PF，将不同种群的搜索信息结合起来以产生良好的解决方案是有用的。因此，对存档的解决方案执行使用 DE 算法的扩展过程以产生 |A|/2 个解，其中| A|表示存档中的解决方案数。

首先从存档中随机选择一个解 Ak = [Ak，1,...,Ak，D]，然后根据公式产生新解

在每一代结束时,扩展过程生成的解决方案将与所有种群以及存档解决方案相结合一起更新存档A.

如果数量超出就采用NSGA-III中基于参考点的选择出高多样性的解决方案进行存储.

B.Environmental Change Detection Procedure(环境变化检测程序) 

为了检测环境变化,每一代都会重新评估预定义的解决方案.由于一次迭代中包括M个种群更新程序和一个扩展过程,因此会产生M+1个解决方案,并针对每个种群更新和扩展过程重新评估其中一个解决方案.

就是将预定义的解表示为B1-BM+1,更新种群之前重新评估Bj,在扩展过程之前重新评估BM+1,

B1、B2 和 B3 被设置为决策空间中的典型位置，即在边界和中心 B1 = [LB1,...,LBD]、B2 = [UB1,...,UBD] 和 B3 = [（LB1 + UB1）/2,...,（LBD + UBD）/2]，其中 LBd 和 UBd 是维度 d 的下限和上限

其余的 （M − 2） 解是从决策空间中随机抽样的。如果一个重新评估的解决方案的适应度值发生变化，则认为环境发生了变化。因此，在一次迭代中，M + 1 解决方案被重新评估以检测环境变化

C.Prediction Strategy(预测策略)

由于种群中的个体通常是PF上不同的最优解，因此PF中心的变化被用作适应不同个体的扰动。在这里，我们将每个目标的最优解称为“注意力点”，将PF中心称为“扰动点”

假设当前环境为 t，在最后两个环境中找到的解集表示为 At−2 和 At−1。对于每个目标 j，分别从 At−2 和 At−1 中选择 fj（X） 上的最佳解，并表示为 Ct−2 j 和 Ct−1 j。

如果有多个解决方案在第 j 个目标上表现最佳，则以这些解决方案的中心为关注点。同样，At−2 和 At−1 的中心分别表示为 Ct−2 M+1 和 Ct−1 M+1。然后，这些注意点和扰动点用于估计目标函数的变化以进行预测。

用公式13计算前两个环境中每个目标的变化和扰动点.

如上所述，个体在种群中Pj的变化可以指其注意力目标Ij和扰动点IM+1的变化。Ij 和 IM+1 的权重可以根据它们在第 j 个目标的子空间中与个体的距离来设置，因为个体的变化与其相邻解的变化更密切相关。 

我们首先对每个单独的 Xj，i、注意力点和扰动点的适应度值 （Ct−1 j ∀1 ≤ j ≤ M + 1） 进行归一化。总体j中Xj，i的适应度值归一化为：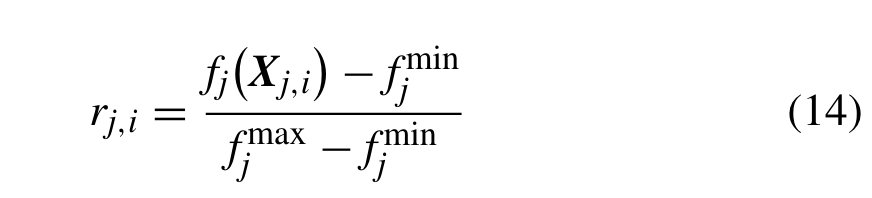 

其中 f max j 和 f min j 分别表示在环境 t −1 中设置的解的第 j 个目标的最大和最小适应度值。Ct−1 j （1 ≤ j ≤ M） 的适应度值最小，归一化为 0。Ct−1 M+1的适应度值未知，但可能位于目标空间的中心，因此归一化为0.5。 

后来，每个单独的 Xj，进行预测.其中w1,w2为权重值

预测策略更新每个种群中的个体以适应环境变化,下图显示了双目标的DMOP预测策略示例.

 

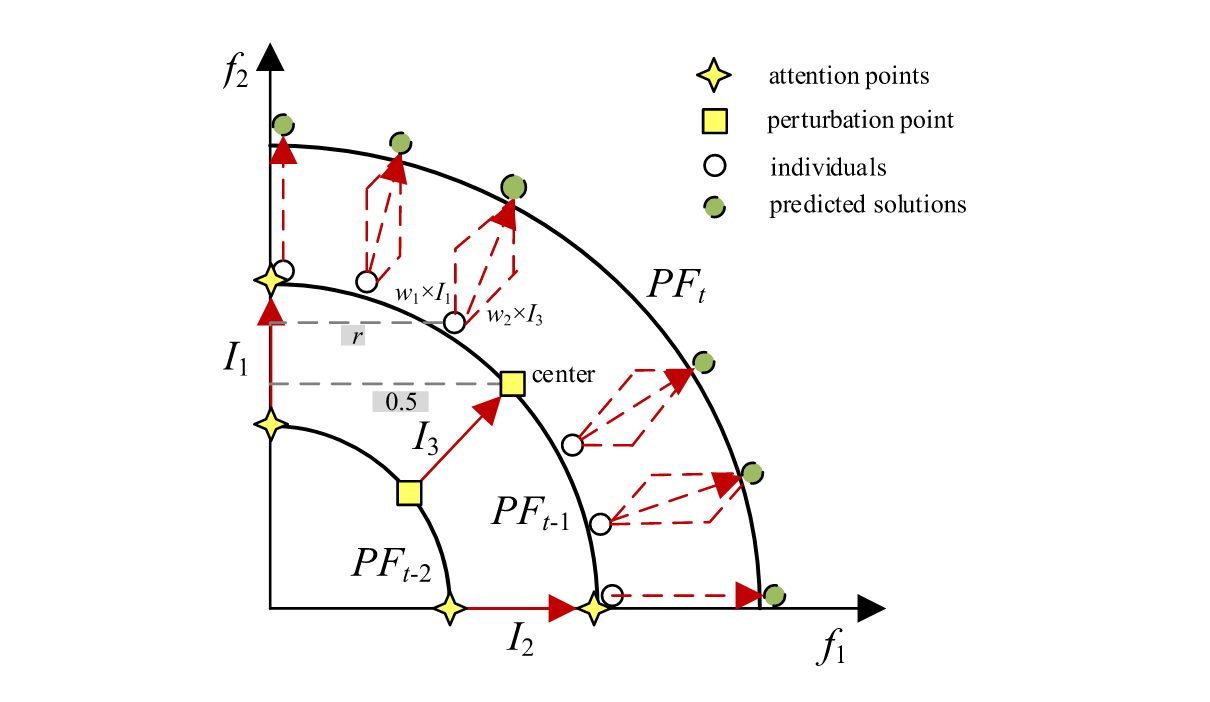
该预测策略旨在为多个群体提供高质量的解决方案来适应变化，但不能准确预测新的PF。

一旦检测到环境变化,就要重新评估所有种群和存档的解决方案,即种群的每个个体X都适用上面的预测策略生成一个新的解X‘,如果X'有更好的适应度值则个体被更新,否则就不变.

整体算法伪代码如图所示