专注 效率 记忆
预习 笔记 复习 做题

欢迎观看我的博客，如有问题交流，欢迎评论区留言，一定尽快回复！（大家可以去看我的专栏，是所有文章的目录）
　
文章字体风格：
红色文字表示：重难点★✔
蓝色文字表示：思路以及想法★✔
　
如果大家觉得有帮助的话，感谢大家帮忙
点赞！收藏！转发！

本博客带大家一起学习，我们不图快，只求稳扎稳打。
由于我高三是在家自学的，经验教训告诉我，学习一定要长期积累，并且复习，所以我推出此系列。
只求每天坚持40分钟，一周学5天，复习2天
也就是一周学10道题
50天后我们就可以学完76道题，相信50天后，我们一定可以有扎实的代码基础！我们每天就40分钟，和我一起坚持下去吧！
qq群：866984458

本题出自 acwing网站
这个系列是免费的
打卡即刻退回费用。

72. 求1+2+…+n【递归】

(递归) O(n)
最直接的想法就是用递归，sum(n) = n+sum(n-1)，但是要注意终止条件，由于求的是1+2+…+n的和，所以需要在n=0的时候跳出递归，但是题目要求不能使用if,while等分支判断，可以考虑利用&&短路运算来终止判断。

时间复杂度分析：递归，复杂度为O(n)。

class Solution {
public:int getSum(int n) {int res = n;n > 0 && (res += getSum(n - 1));return res;}
};

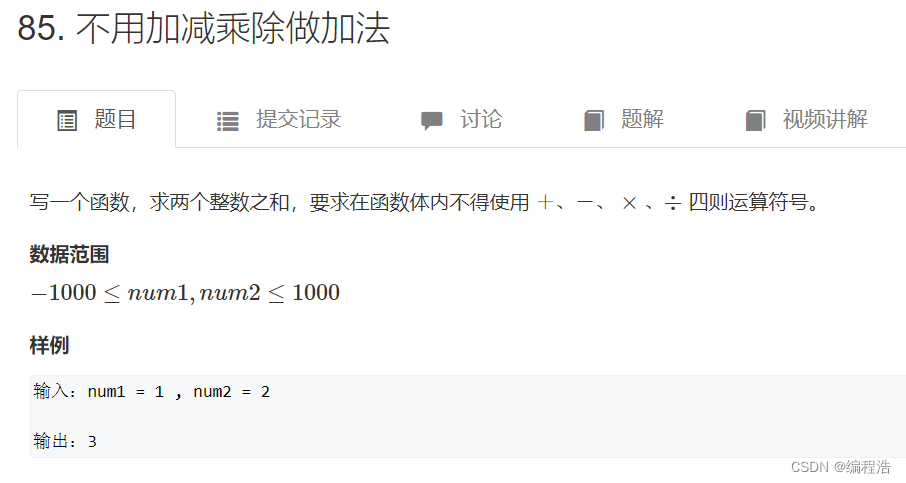
73. 不用加减乘除做加法【二进制 加法】

int sum = num1 ^ num2;//不进位的加法

int carry = (num1 & num2)<<1;//进位

class Solution {
public:int add(int num1, int num2){while(num2!=0){int sum = num1 ^ num2;//不进位的加法int carry = (num1 & num2)<<1;//进位num1 = sum;num2 = carry;}return num1;}
};

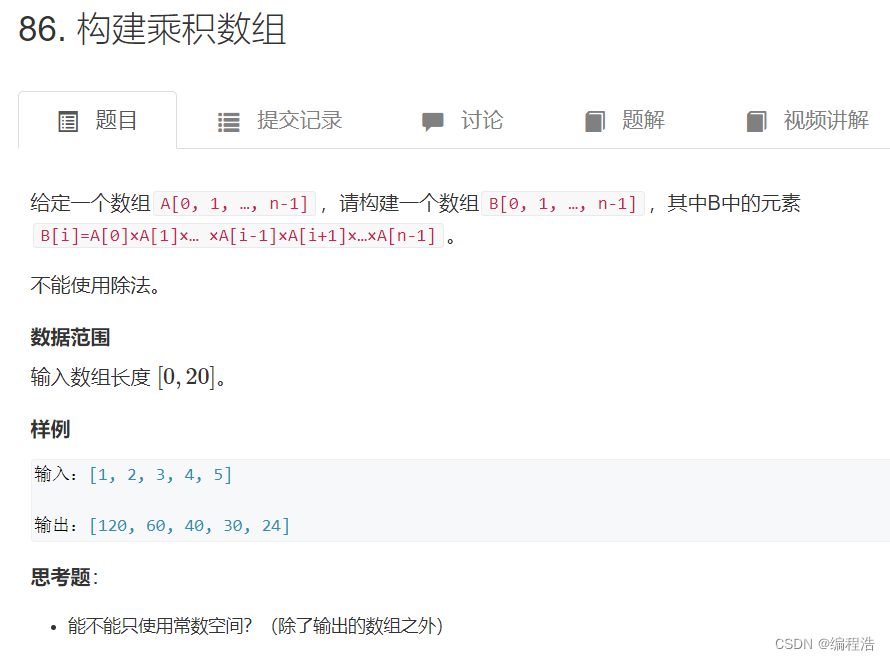
74. 构建乘积数组

(动归) O(n)
用两个数组left和right，left[i]=A[0]A[1]…*A[i-1], left[i]=A[i-1]*left[i-1]; right[i] = A[i+1]A[i+2]…*A[n-1]，则right[i]=A[i+1]*right[i+1]。

最后结果B[i]=left[i]*right[i]。

时间复杂度分析：需要遍历数组，复杂度为O(n)

class Solution {
public:vector<int> multiply(const vector<int>& A) {vector<int>left(A.size(),1);vector<int>right(A.size(),1);for(int i = 1;i<A.size();i++){left[i] = A[i-1]*left[i-1];}for(int i = A.size()-2;i>=0;i--){right[i] = A[i+1]*right[i+1];}vector<int>B(A.size(),0);for(int i = 0;i<A.size();i++){B[i] = left[i]*right[i];}return B;}
};