【Python】python实现决策树算法和贝叶斯算法(附源代码）

使用一种你熟悉的程序设计语言，实现（1）贝叶斯算法和（2）决策树算法

目录

  • 1、贝叶斯算法
  • 2、决策树算法
  • 3、两种算法比较

1、贝叶斯算法

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from collections import defaultdict
import collections
import math
import pickle
import operatoroutlook = ["晴朗", "多云","雨天"]
Temperature = ["高温", "中温","低温"]
Humidity = ["高湿","一般"]
Wind = ["大", "小"]
PlayTennis=["是","否"]
Play = []
Play.append(outlook)
Play.append(Temperature)
Play.append(Humidity)
Play.append(Wind)
Play.append(PlayTennis)#数据集
data = [  ["晴朗","高温","高湿","小","否"],["晴朗","高温","高湿","大","否"],["多云","高温","高湿","小","是"],["雨天","中温","高湿","小","是"],["雨天","低温","一般","小","是"],["雨天","低温","一般","大","否"],["多云","低温","一般","大","是"],["晴朗","中温","高湿","小","否"],["晴朗","低温","一般","小","是"],["雨天","中温","一般","小","是"],["晴朗","中温","一般","大","是"],["多云","中温","高湿","大","是"],["晴朗","高温","一般","小","是"],["多云", "高温", "一般", "小", "是"],["雨天","中温","高湿","大","否"],["晴朗","中温","高湿","大","否"]]length = len(data)
#划分数据集，将1-12条作为训练数据集，13-16作为测试数据集
train = data[:12]
train_length = len(train)
print("训练数据集")
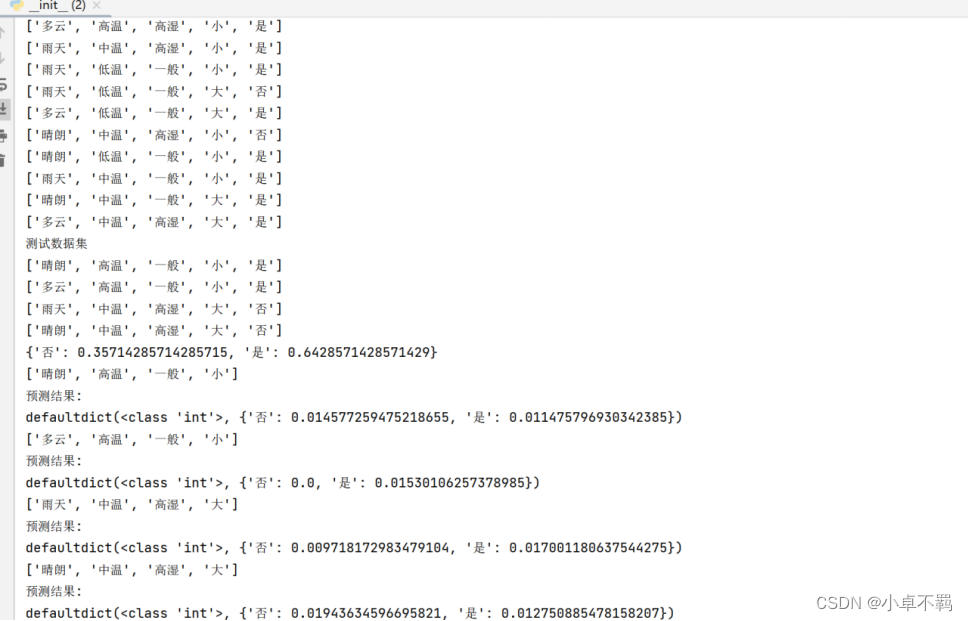
for i in range(train_length):print(train[i])
test= data[12:]
test_length = len(test)
print("测试数据集")
for i in range(test_length):print(test[i])
def count_PlayTennis_total(data):count = defaultdict(int)for i in range(train_length):count[data[i][4]]+=1return count#先验概率
def cal_base_rates(data):y = count_PlayTennis_total(data)cal_base_rates = {}for label in y.keys():priori_prob = (y[label]+1) / (len(train)+2)cal_base_rates[label] = priori_probreturn cal_base_ratesprint(cal_base_rates(train))def count_sj(attr, Play):for i in range(len(Play)):if attr in Play[i]:return len(Play[i])#似然概率p(x|y) 也叫条件概率
def likelihold_prob(data):#计算各个特征值在已知结果下的概率（likelihood probabilities）y = count_PlayTennis_total(data)likelihold = {}for i,c in y.items():#创建一个临时的字典，临时存储各个特征值的概率attr_prob = defaultdict(int)for j in range(train_length):if data[j][4]==i:for attr in range(4):attr_prob[data[j][attr]]+=1for keys,values in attr_prob.items():sj =  count_sj(keys, Play)attr_prob[keys]=(values+1)/(c+sj)likelihold[i] = attr_probreturn likeliholdLikeHold = likelihold_prob(train)def Test(data,test):y = count_PlayTennis_total(data)likehold = likelihold_prob(data)playtennis = cal_base_rates(data)RATE = defaultdict(int)print(test)for i, _ in y.items():rates=1for j in range(4):attr = test[j]rates *= likehold[i][attr]rates=rates * playtennis[i]RATE[i] = ratesprint("预测结果: " )print(RATE)return sorted(RATE,key=lambda x:RATE[x])[-1]#先验概率
cal_base_rates(train)
# 条件概率
likelihold_prob(train)
Test(train,test[0][:4])
Test(train,test[1][:4])
Test(train,test[2][:4])
Test(train,test[3][:4])

在这里插入图片描述

2、决策树算法

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from collections import defaultdict
import collections
import math
import pickle
import operator# 定义属性值
outlook = ["晴朗", "多云", "雨天"]
Temperature = ["高温", "中温", "低温"]
Humidity = ["高湿", "一般"]
Wind = ["大", "小"]
PlayTennis = ["是", "否"]
Play = []
Play.append(outlook)
Play.append(Temperature)
Play.append(Humidity)
Play.append(Wind)
Play.append(PlayTennis)# 数据集
data = [["晴朗", "高温", "高湿", "小", "否"],["晴朗", "高温", "高湿", "大", "否"],["多云", "高温", "高湿", "小", "是"],["雨天", "中温", "高湿", "小", "是"],["雨天", "低温", "一般", "小", "是"],["雨天", "低温", "一般", "大", "否"],["多云", "低温", "一般", "大", "是"],["晴朗", "中温", "高湿", "小", "否"],["晴朗", "低温", "一般", "小", "是"],["雨天", "中温", "一般", "小", "是"],["晴朗", "中温", "一般", "大", "是"],["多云", "中温", "高湿", "大", "是"],["晴朗", "高温", "一般", "小", "是"],["多云", "高温", "一般", "小", "是"],["雨天", "中温", "高湿", "大", "否"],["晴朗", "中温", "高湿", "大", "否"]]length = len(data)
# 划分数据集，将1-12条作为训练数据集，13-16作为测试数据集
train = data[:12]
train_length = len(train)
print("训练数据集")
for i in range(train_length):print(train[i])
test = data[12:]
test_length = len(test)
print("测试数据集")
for i in range(test_length):print(test[i])# 计算信息熵
def cal_entropy(dataset):length = len(dataset)entropy = 0count = {}for i in dataset:label = i[-1]count[label] = count.get(label, 0) + 1for key in count:p = count[key] / lengthentropy = entropy - p * math.log(p, 2)return entropy# 划分数据集
def splitDataSet(dataSet, axis, value):childDataSet = []for i in dataSet:if i[axis] == value:childList = i[:axis]childList.extend(i[axis + 1:])childDataSet.append(childList)# print(childDataSet)return childDataSet# 选择最好的特征
def chooseFeature(dataset):old_entropy = cal_entropy(dataset)character = -1for i in range(len(dataset[0]) - 1):newEntropy = 0featureList = [word[i] for word in dataset]value = set(featureList)for j in value:childDataSet = splitDataSet(dataset, i, j)newEntropy += len(childDataSet) / len(dataset) * cal_entropy(childDataSet)if (newEntropy < old_entropy):character = iold_entropy = newEntropyreturn character# 当遍历完所有特征时，用于选取当前数据集中最多的一个类别代表该类别
def most(classList):classCount = {}for i in range(len(classList)):classCount[i] = classCount.get(i, 0) + 1sortCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)# print(sortCount)return sortCount[0][0]# 构造决策树
def createDT(dataSet, labels):# print(dataSet)tempLabels = labels[:]classList = [word[-1] for word in dataSet]if classList.count(classList[0]) == len(classList):return classList[0]if len(dataSet[0]) == 1:return most(dataSet)character = chooseFeature(dataSet)node = tempLabels[character]myTree = {node: {}}del (tempLabels[character])featureList = [word[character] for word in dataSet]value = set(featureList)for i in value:newLabels = tempLabelsmyTree[node][i] = createDT(splitDataSet(dataSet, character, i), newLabels)return myTree# 分类
def classify(dTree, labels, testData):node = list(dTree.keys())[0]condition = dTree[node]labelIndex = labels.index(node)classLabel = Noneprint(testData)for key in condition:if testData[labelIndex] == key:if type(condition[key]).__name__ == 'dict':# print("预测结果: " )classLabel = classify(condition[key], labels, testData)else:print("预测结果: ")classLabel = condition[key]return classLabel# 用于将构建好的决策树保存，方便下次使用
def stroeTree(myTree, filename):f = open(filename, 'wb')pickle.dump(myTree, f)f.close()# 载入保存的决策树
def loadTree(filename):f = open(filename, 'rb')return pickle.load(f)labels = ['天气状况', '温度', '湿度', '风力', '是否适合游玩（预测变量）']
myTree = createDT(train, labels)
stroeTree(myTree, '1')
myTree = loadTree('1')
print(myTree)

在这里插入图片描述

3、两种算法比较

决策树算法和贝叶斯算法都是常见的机器学习算法，用于分类和预测任务，但它们的工作原理和应用场景有所不同。以下是它们之间的比较：

决策树算法贝叶斯算法
工作原理基于对输入数据集进行递归分割，每次分割都基于某个特征的某个阈值，以最小化节点的不纯度（如基尼系数、信息增益等）。这种递归分割形成了一个树形结构，每个叶子节点代表一个类别或一个预测结果。基于贝叶斯定理，利用已知的数据集和特征之间的关系来计算给定一个新样本属于每个类别的概率。它假设特征之间相互独立，然后利用贝叶斯公式计算后验概率，从而进行分类。
应用场景适用于具有离散和连续特征的分类问题，特别是当特征之间存在复杂关系时。它易于理解和解释，并且对异常值和缺失值有较好的鲁棒性。适用于处理高维数据和文本分类等问题。它在样本量较少时表现良好，并且对噪声数据有一定的鲁棒性
优点易于理解、处理离散和连续数据、对异常值和缺失值具有鲁棒性容易过拟合、对数据分布敏感以及不稳定性
缺点对小样本数据有效、对噪声数据有一定的鲁棒性、能够处理高维数据对特征之间相互独立的假设较强、在特征相关性较高时表现不佳
模型解释易于解释和可视化，可以通过树结构直观地理解每个决策的依据通常较为复杂，不太容易直接解释，因为它涉及到对多个特征之间的概率关系进行建模

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/536232.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Apache Paimon系列之：认识Paimon

Apache Paimon系列之：认识Paimon

Apache Paimon系列之&#xff1a;认识Paimon 一、认识Paimon二、统一存储三、基本概念1.文件布局2.Snapshot3.清单文件4.数据文件5.分区6.一致性保证 一、认识Paimon Apache Paimon的架构&#xff1a; 如上架构所示&#xff1a; 读/写&#xff1a;Paimon 支持多种读/写数据和…
阅读更多...
Mybatis 实体类类型参数传入sql语句

Mybatis 实体类类型参数传入sql语句

1.Mapper接口中抽象方法的声明&#xff0c;将实体信息传入到数据库表中。 int insertEmployee(Employee employee);2.SQL语句 <insert id"insertEmployee">insert into t_emp(emp_name,emp_salary) values(#{empName},#{empSalary}) </insert>3.对应关…
阅读更多...
媒体单位专用小记者报名及各类活动报名系统介绍

媒体单位专用小记者报名及各类活动报名系统介绍

媒体单位专用小记者报名及各类活动报名系统介绍 小记者活动鼓励孩子们关注生活和社会&#xff0c;丰富成长体验&#xff0c;开启心智&#xff0c;淬砺思想。这不仅有助于提高他们的理性思辨力&#xff0c;还能培养他们的社会责任感和公民意识。小记者活动为学生提供了一个全新…
阅读更多...
C语言易错知识点：scanf函数

C语言易错知识点：scanf函数

scanf在C语言学习中比较常用&#xff0c;但因为其涉及屏幕缓冲区导致有的时候会调入陷阱&#xff0c;下面分享一下常见的需要注意的事项&#xff1a; 1.输入末尾带有回车\n 当我们输入数据后&#xff0c;最后按下回车时&#xff0c;屏幕缓冲区的末尾都会含有这个字符 scanf的…
阅读更多...
String类及其常用方法

String类及其常用方法

文章目录 1.String类的特性与使用1.1 String类的特性1.2 String对象的创建方式1.3 String 的使用&#xff08;不同的拼接操作&#xff09; 2.String常用方法2.1 String的常用方法一2.2 String常用方法二2.3 String常用方法三 1.String类的特性与使用 1.1 String类的特性 Stri…
阅读更多...
Linux常用操作命令

Linux常用操作命令

Linux常用操作命令 1.文件管理catfile 2.文档编辑3.文件传输4.磁盘管理5.磁盘维护6.网络通讯7.系统管理8.系统设置9.备份压缩10.设备管理 Linux 英文解释为 Linux is not Unix。 Linux内核最初只是由芬兰人李纳斯托瓦兹&#xff08;Linus Torvalds&#xff09;在赫尔辛基大学上…
阅读更多...
高铁列车员信息宣传向媒体投稿有哪些方法？

高铁列车员信息宣传向媒体投稿有哪些方法？

作为一名高铁列车工作人员,我肩负着传递高铁精神、展示列车员风采的重要使命。每月,我都要完成单位对外信息宣传的考核任务,通过媒体投稿来发表列车员的信息宣传文章。在这条信息宣传之路上,我经历了从摸着石头过河到智慧投稿的蜕变,其中的心酸与轻松交织,成为了我职业生涯中难…
阅读更多...
值得收藏的Python字符串操作大总结！

值得收藏的Python字符串操作大总结！

今天给大家总结一下字符串的所有操作&#xff0c;string替换、删除、截取、复制、连接、比较、查找、包含、大小写转换、分割等。 去空格及特殊符号 s.strip().lstrip().rstrip(,) 复制字符串 #strcpy(sStr1,sStr2) sStr1 strcpy sStr2 sStr1 sStr1 strcpy2 print sStr2 连…
阅读更多...
【WSN覆盖优化】基于改进黏菌算法的无线传感器网络覆盖 WSN覆盖优化【Matlab代码#65】

【WSN覆盖优化】基于改进黏菌算法的无线传感器网络覆盖 WSN覆盖优化【Matlab代码#65】

文章目录 【可更换其他算法&#xff0c;获取资源请见文章第5节&#xff1a;资源获取】1. 改进SMA算法1.1 改进参数p1.2 混沌精英突变策略 2. WSN节点感知模型3. 部分代码展示4. 仿真结果展示5. 资源获取 【可更换其他算法&#xff0c;获取资源请见文章第5节&#xff1a;资源获取…
阅读更多...
netty草图笔记

netty草图笔记

学一遍根本记不住&#xff0c;那就再学一遍 public static void test_nettyFuture() {NioEventLoopGroup group new NioEventLoopGroup();log.info("开始提交任务");Future<String> future group.next().submit(() -> {log.info("执行异步任…
阅读更多...
6.Java并发编程—深入剖析Java Executors：探索创建线程的5种神奇方式

6.Java并发编程—深入剖析Java Executors：探索创建线程的5种神奇方式

Executors快速创建线程池的方法 Java通过Executors 工厂提供了5种创建线程池的方法&#xff0c;具体方法如下 方法名描述newSingleThreadExecutor()创建一个单线程的线程池&#xff0c;该线程池中只有一个工作线程。所有任务按照提交的顺序依次执行&#xff0c;保证任务的顺序性…
阅读更多...
代码随想录-java-栈与队列总结

代码随想录-java-栈与队列总结

栈&#xff08;Stack&#xff09;&#xff1a;是只允许在一端进行插入或删除的线性表。栈是一种线性表&#xff0c;限定这种线性表只能在某一端进行插入和删除操作。进行操作的这一端称为栈顶。 队列&#xff08;Queue&#xff09;是只允许在一端进行插入操作&#xff0c;而在另…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023