目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.代码实现
- 4.参考文献
1.背景
2017年,Zhao等人受到蝠鲼自然捕食行为启发,提出了蝠鲼觅食优化算法(Manta Ray Foraging Optimization,MRFO)。
2.算法原理
2.1算法思想
MRFO模拟了蝠鲼在海洋中的觅食过程,提出了三种捕食策略链式觅食-螺旋觅食-翻滚觅食。
2.2算法过程
链式觅食:
蝠鲼可以观察到浮游生物的位置并朝它游去,在一个位置上浮游生物的浓度越高,位置越好(适应度函数)。蝠鲼排成一列,形成觅食链,除了第一个个体外,其他个体不仅朝着食物游去,还朝着它前面的个体游去。在每次迭代中,每个个体都会根据迄今为止找到的最佳解决方案和它前面的解决方案进行更新。
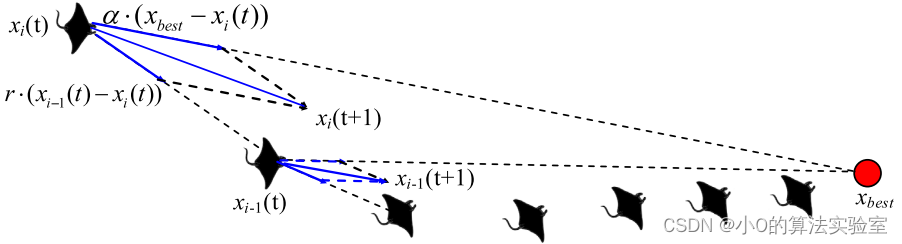
x i d ( t + 1 ) = { x i d ( t ) + r ⋅ ( x b e s t d ( t ) − x i d ( t ) ) + α ⋅ ( x b e s t d ( t ) − x i d ( t ) ) i = 1 x i d ( t ) + r ⋅ ( x i − 1 d ( t ) − x i d ( t ) ) + α ⋅ ( x b e s t d ( t ) − x i d ( t ) ) i = 2 , … , N x_i^d(t+1)=\begin{cases}x_i^d(t)+r\cdot(x_{best}^d(t)-x_i^d(t))+\alpha\cdot(x_{best}^d(t)-x_i^d(t))&i=1\\x_i^d(t)+r\cdot(x_{i-1}^d(t)-x_i^d(t))+\alpha\cdot(x_{best}^d(t)-x_i^d(t))&i=2,\ldots,N\end{cases} xid(t+1)={xid(t)+r⋅(xbestd(t)−xid(t))+α⋅(xbestd(t)−xid(t))xid(t)+r⋅(xi−1d(t)−xid(t))+α⋅(xbestd(t)−xid(t))i=1i=2,…,N
a a a为控制因子,表述为:
α = 2 ⋅ r ⋅ ∣ l o g ( r ) ∣ \alpha=2\cdot r\cdot\sqrt{|log(r)|} α=2⋅r⋅∣log(r)∣
螺旋觅食:
当一群蝠鲼在深水中发现一片浮游生物时,它们会组成一条长长的觅食链,并以螺旋形式向食物游去。(类似于鲸鱼算法(WOA)捕食策略)
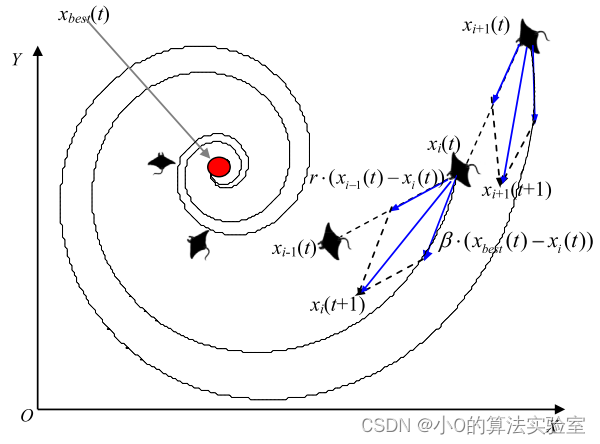
当 t / T > r a n d 时 t/T>rand时 t/T>rand时,此时进行全局探索:
x i d ( t + 1 ) = { x b e s t d + r ⋅ ( x b e s t d ( t ) − x i d ( t ) ) + β ⋅ ( x b e s t d ( t ) − x i d ( t ) ) i = 1 x b e s t d + r ⋅ ( x i − 1 d ( t ) − x i d ( t ) ) + β ⋅ ( x b e s t d ( t ) − x i d ( t ) ) i = 2 , … , N x_i^d(t+1)=\begin{cases}x_{best}^d+r\cdot(x_{best}^d(t)-x_i^d(t))+\beta\cdot(x_{best}^d(t)-x_i^d(t))&i=1\\x_{best}^d+r\cdot(x_{i-1}^d(t)-x_i^d(t))+\beta\cdot(x_{best}^d(t)-x_i^d(t))&i=2,\dots,N\end{cases} xid(t+1)={xbestd+r⋅(xbestd(t)−xid(t))+β⋅(xbestd(t)−xid(t))xbestd+r⋅(xi−1d(t)−xid(t))+β⋅(xbestd(t)−xid(t))i=1i=2,…,N
当 t / T ≥ r a n d 时 t/T \ge rand时 t/T≥rand时,此时进行局部探索:
x i d ( t + 1 ) = { x r a n d d + r ⋅ ( x r a n d d − x i d ( t ) ) + β ⋅ ( x r a n d d − x i d ( t ) ) i = 1 x r a n d d + r ⋅ ( x i − 1 d ( t ) − x i d ( t ) ) + β ⋅ ( x r a n d d − x i d ( t ) ) i = 2 , … , N \left.x_{i}^{d}(t+1)=\left\{\begin{array}{ll}{{x_{rand}^{d}+r\cdot(x_{rand}^{d}-x_{i}^{d}(t))+\beta\cdot(x_{rand}^{d}-x_{i}^{d}(t))}}&{i=1}\\{{x_{rand}^{d}+r\cdot(x_{i-1}^{d}(t)-x_{i}^{d}(t))+\beta\cdot(x_{rand}^{d}-x_{i}^{d}(t))}}&{i=2,\ldots,N}\end{array}\right.\right. xid(t+1)={xrandd+r⋅(xrandd−xid(t))+β⋅(xrandd−xid(t))xrandd+r⋅(xi−1d(t)−xid(t))+β⋅(xrandd−xid(t))i=1i=2,…,N
β \beta β为控制因子,表述为:
β = 2 e r 1 T − t + 1 T ⋅ sin ( 2 π r 1 ) \beta=2e^{r_1\frac{T-t+1}T}\cdot\sin(2\pi r_1) β=2er1TT−t+1⋅sin(2πr1)
翻滚觅食:
在这种行为中,食物的位置被视为一个中心点。每个个体倾向于在中心点周围来回游动,并翻滚到一个新的位置。
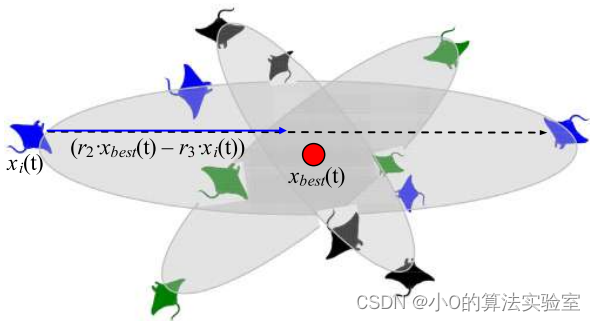
x i d ( t + 1 ) = x i d ( t ) + S ⋅ ( r 2 ⋅ x b e s t d − r 3 ⋅ x i d ( t ) ) , i = 1 , … , N x_i^d(t+1)=x_i^d(t)+S\cdot(r_2\cdot x_{best}^d-r_3\cdot x_i^d(t)),i=1,\ldots,N xid(t+1)=xid(t)+S⋅(r2⋅xbestd−r3⋅xid(t)),i=1,…,N
伪代码:

3.代码实现
% 蝠鲼觅食优化算法
function [Best_pos, Best_fitness, Iter_curve, History_pos, History_best] = MRFO(pop, maxIter,lb,ub,dim,fobj)
%input
%pop 种群数量
%dim 问题维数
%ub 变量上边界
%lb 变量下边界
%fobj 适应度函数
%maxIter 最大迭代次数
%output
%Best_pos 最优位置
%Best_fitness 最优适应度值
%Iter_curve 每代最优适应度值
%History_pos 每代种群位置
%History_best 每代最优个体位置
%% 初始化种群
PopPos = zeros(pop, dim);
for i = 1:dimPopPos(:,i) = lb(i) + (ub(i) - lb(i)) * rand(pop, 1);
end
%% 计算适应度
PopFit = zeros(1, pop);
for i=1:popPopFit(i)=fobj(PopPos(i,:));
end
%% 记录
[MinFitness, MinIdx] = sort(PopFit);
Best_pos = PopPos(MinIdx(1),:);
Best_fitness = MinFitness(1);
%% 迭代
for It = 1:maxIter Coef = It / maxIter; if rand<0.5r1=rand; Beta=2*exp(r1*((maxIter-It+1)/maxIter))*(sin(2*pi*r1)); if Coef > rand newPopPos(1,:)=Best_pos+rand(1,dim).*(Best_pos-PopPos(1,:))+Beta*(Best_pos-PopPos(1,:)); %Equation (4)elseIndivRand=rand(1,dim).*(ub-lb)+lb; newPopPos(1,:)=IndivRand+rand(1,dim).*(IndivRand-PopPos(1,:))+Beta*(IndivRand-PopPos(1,:)); %Equation (7) end else Alpha=2*rand(1,dim).*(-log(rand(1,dim))).^0.5; newPopPos(1,:)=PopPos(1,:)+rand(1,dim).*(Best_pos-PopPos(1,:))+Alpha.*(Best_pos-PopPos(1,:)); %Equation (1)endfor i=2:popif rand<0.5r1=rand; Beta=2*exp(r1*((maxIter-It+1)/maxIter))*(sin(2*pi*r1)); if Coef>rand newPopPos(i,:)=Best_pos+rand(1,dim).*(PopPos(i-1,:)-PopPos(i,:))+Beta*(Best_pos-PopPos(i,:)); %Equation (4)elseIndivRand=rand(1,dim).*(ub-lb)+lb; newPopPos(i,:)=IndivRand+rand(1,dim).*(PopPos(i-1,:)-PopPos(i,:))+Beta*(IndivRand-PopPos(i,:)); %Equation (7) end elseAlpha=2*rand(1,dim).*(-log(rand(1,dim))).^0.5; newPopPos(i,:)=PopPos(i,:)+rand(1,dim).*(PopPos(i-1,:)-PopPos(i,:))+Alpha.*(Best_pos-PopPos(i,:)); %Equation (1)end endfor i=1:pop% 边界检查H_ub=newPopPos(i,:)>ub;H_lb=newPopPos(i,:)<lb;newPopPos(i,:)=(newPopPos(i,:).*(~(H_ub+H_lb)))+ub.*H_ub+lb.*H_lb; newPopFit(i)=fobj(newPopPos(i,:)); if newPopFit(i)<PopFit(i)PopFit(i)=newPopFit(i);PopPos(i,:)=newPopPos(i,:);endendS=2;for i=1:pop newPopPos(i,:)=PopPos(i,:)+S*(rand*Best_pos-rand*PopPos(i,:)); %Equation (8)endfor i=1:pop% 边界检查H_ub=newPopPos(i,:)>ub;H_lb=newPopPos(i,:)<lb;newPopPos(i,:)=(newPopPos(i,:).*(~(H_ub+H_lb)))+ub.*H_ub+lb.*H_lb; newPopFit(i)=fobj(newPopPos(i,:)); if newPopFit(i)<PopFit(i)PopFit(i)=newPopFit(i);PopPos(i,:)=newPopPos(i,:);endendfor i=1:popif PopFit(i)<Best_fitnessBest_fitness=PopFit(i);Best_pos=PopPos(i,:); endendIter_curve(It)=Best_fitness;History_pos{It} = PopPos;History_best{It} = Best_pos;
end
end
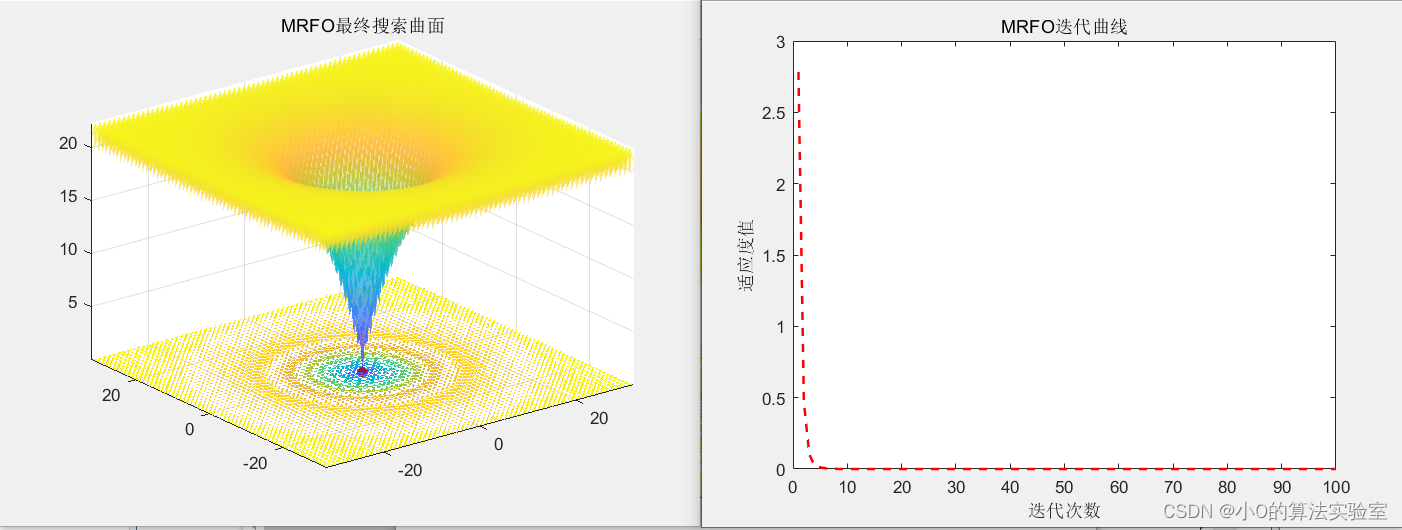
4.参考文献
[1] Zhao W, Zhang Z, Wang L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications[J]. Engineering Applications of Artificial Intelligence, 2020, 87: 103300.



![[java入门到精通] 20 反射精讲](https://img-blog.csdnimg.cn/direct/a75c94c715fe43c389a994437951f2fd.png)