力扣日记:【贪心算法篇】376. 摆动序列
日期:2024.3.14
参考:代码随想录、力扣
376. 摆动序列
题目描述
难度:中等
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
- 例如, [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ,因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
- 相反,[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
示例 1:
输入:nums = [1,7,4,9,2,5]
输出:6
解释:整个序列均为摆动序列,各元素之间的差值为 (6, -3, 5, -7, 3) 。
示例 2:
输入:nums = [1,17,5,10,13,15,10,5,16,8]
输出:7
解释:这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ,各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。
示例 3:
输入:nums = [1,2,3,4,5,6,7,8,9]
输出:2
提示:
- 1 <= nums.length <= 1000
- 0 <= nums[i] <= 1000
进阶:你能否用 O(n) 时间复杂度完成此题?
题解
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {// 将数字数列以数值大小作为高度排列,可以发现:当出现一次波峰或波谷,摆动子序列的长度可+1// 而波谷波峰之间的其他数字,不影响摆动子序列的长度// 所以关键在于// 1. 寻找波峰(prediff > 0 && curdiff < 0)以及波谷(prediff < 0 && curdiff > 0)// 2. 除此之外,还要考虑存在平坡的特殊情况,如对于1,2,2,2,1 可算作含有一个波峰;或对于2,1,1,1,2 可视为含有一个波谷// 对此,两者可统一用“先平后陡为峰或谷(或反之)”,则波峰波谷可分别用 prediff>=0 && curdiff<0 和 prediff<=0 && curdiff>0 表示// 3. 最后是序列首部:由于波峰及波谷的数目+2才为实际长度,除去初始count=1,可在序列首部添加一个虚拟平坡(即初始prediff=0),则可增加一个虚拟波峰(谷)if (nums.size() <= 1) return nums.size(); // 长度为0、1(也可包含2)直接返回int prediff = 0, curdiff = 0;int count = 1;for (int i = 0; i < nums.size() - 1; i++) { // 注意不能越界// 计算curdiffcurdiff = nums[i + 1] - nums[i];if (prediff >= 0 && curdiff < 0 || prediff <= 0 && curdiff > 0) {count++;prediff = curdiff; // 注意:只有当为波峰或波谷时才更新prediff(避免真正波峰波谷之间的平坡误判)// 实际上这样写了之后,对于 1,2,2,2,1,是通过pre > 0 && cur < 0 判断的}}return count;}
};
复杂度
时间复杂度:O(n)
空间复杂度:O(1)
思路总结
-
思路来源于代码随想录
-
还是不太理解,为什么这种方式是所谓贪心算法?
代码随想录思路:
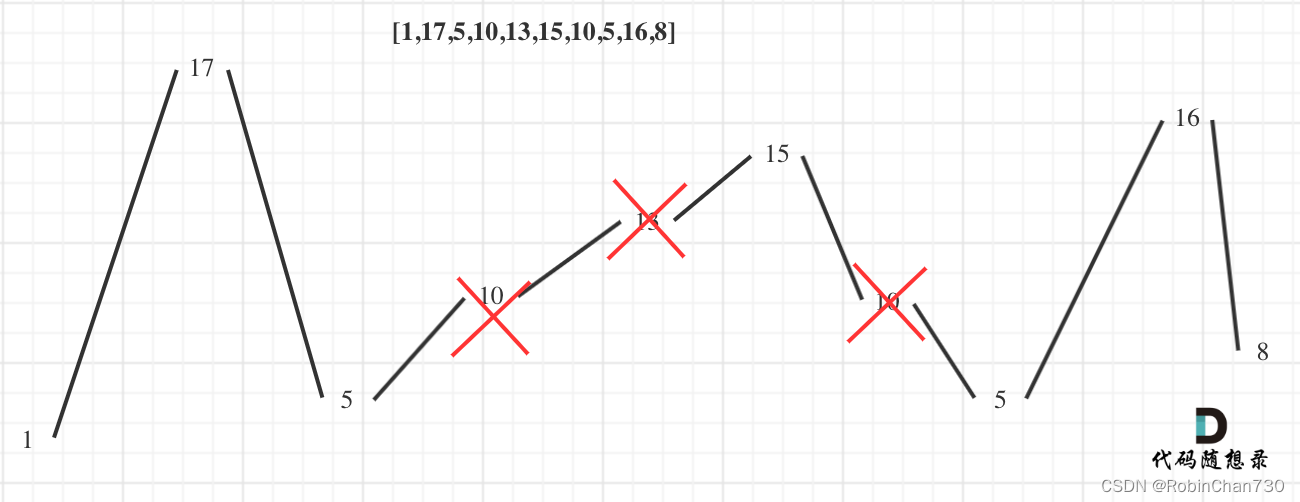
局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。
整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。
-
思路:
- 将数字数列以数值大小作为高度排列(如上图),可以发现:当出现一次波峰或波谷,摆动子序列的长度可+1
- 而波谷波峰之间的其他数字,不影响摆动子序列的长度
- 所以关键在于
-
- 寻找波峰(
prediff > 0 && curdiff < 0)以及波谷(prediff < 0 && curdiff > 0)
- 寻找波峰(
-
- 除此之外,还要考虑存在平坡的特殊情况,如对于1,2,2,2,1 可算作含有一个波峰;或对于2,1,1,1,2 可视为含有一个波谷(即可形成摆动子序列)
对此,两者可统一用“先平后陡为峰/谷”,则波峰波谷可分别用prediff>=0 && curdiff<0和prediff<=0 && curdiff>0表示
- 除此之外,还要考虑存在平坡的特殊情况,如对于1,2,2,2,1 可算作含有一个波峰;或对于2,1,1,1,2 可视为含有一个波谷(即可形成摆动子序列)
-
- 最后是序列首部:由于波峰及波谷的数目+2才为实际长度,除去初始count=1,可在序列首部添加一个虚拟平坡(即初始prediff=0),则可增加一个虚拟波峰(谷)
-
-
TODO: 动态规划