1、汉诺塔
面试题 08.06. 汉诺塔问题 - 力扣(LeetCode)


Why?为什么这个汉诺塔问题可以用递归来解决?
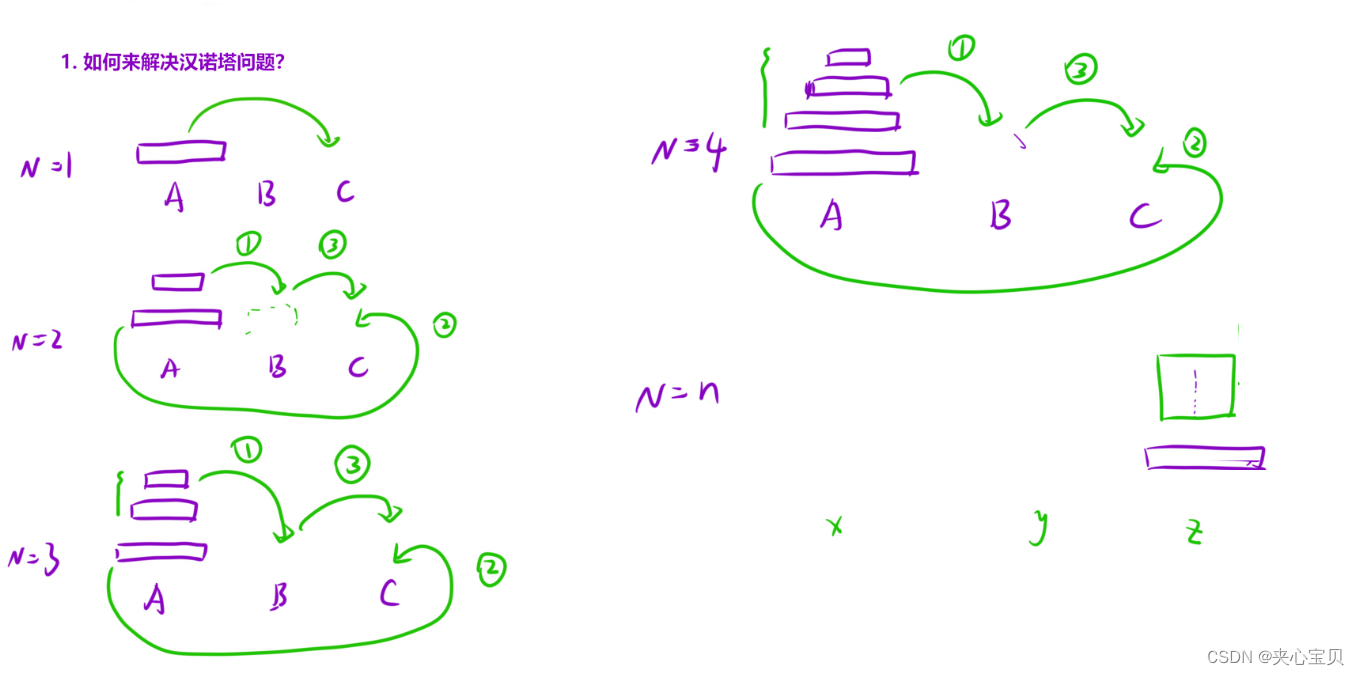
如何来解决汉诺塔问题?
如果N == 1时,A[0] B C,直接将A上的盘子转移到C上面。
如果N == 2时,A[1,0] B C,先将上面所有的盘子放到B,然后将A上最大的那个放到C,再把B上的盘子转移到C。
如果N == 3,先将上面两个盘子,借助C,放到B上,然后把最下面的盘子放到C上,再将B上的两个盘子,借助A,放到C上。那么此时,转移上面两个盘子的操作,是不是和N == 2时的操作一模一样了。相同的子问题就出来了。并且由于A最下面是最大的盘子,那么过程中借助A柱子时,就不用担心大的放到小的上面去了。
如果N == n时,…………
分析可知:
解决本题时,可以分割出子问题,并且子问题的解决方法和主问题相同。
在解决子问题时,分割出子子问题,解决子子问题的时候,方法又和子问题一样。
本题体现:解决N = 4时,出现了N = 3的情况;解决N = 3时,出现了N = 2的情况…………
此时就可以用递归解决。
How?如何编写递归的代码?
1、重复子问题--->函数头
将X柱子上的一堆盘子,借助Y柱子,转移到Z柱子上。
void dfs(X,Y,Z,int n),n代表要转移多少个盘子。
2、只关心某一个子问题在做什么--->函数体
dfs(X,Z,Y,N-1) //将X上面N-1个盘子,借助Z放到Y上。
X.back() --> Z //将X的最后一个盘子,放到Z上。
dfs(Y,X,Z,N-1) //再将Y上所有的N-1个盘子,借助X,放到Z上。
3、递归的出口(哪一个子问题不能再细分了)
当N == 1时,不用借助柱子就能完成,所以递归的出口就是N == 1
if( N == 1) X.back --> Z //X.back()移到Z上。
class Solution {
public:void dfs(vector<int&