概率论与数理统计（随机事件与概率）-编程知识

1随机事件与概率

1.1随机事件及其运算规律

1.1.1运算

交换律
结合律
分配律
德摩根律

1.2概率的定义及其确定方法

1.2.1概率的统计定义

频率设在 n 次试验中，事件 A 发生了 $\mu$ (A)次，则称为事件 A 发生的频率。

1.2.2概率的统计定义

在一组恒定不变的条件下，将某试验重复进行n次，随着n 增大，事件A发生的频率 $f_{n}(A)$ ，总在某一固定常数p 左右摆动，我们称这个稳定值 p 为事件A的概率, 记作 P(A). f (A)

性质：

非负性：

规范性：

可列可加性：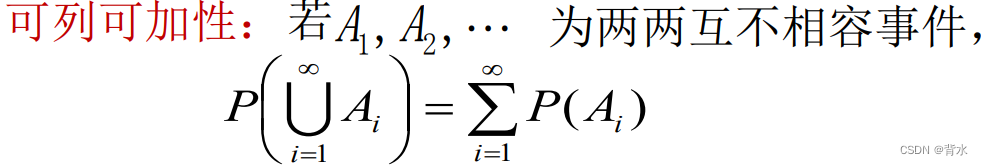

1.2.3确定概率的古典方法

条件：

试验的样本空间只包含有限个元素
试验中每个基本事件发生的可能性相同

古典概率的确定：

设试验 E 的样本空间由n 个样本点构成， A 为 E 的任意一个事件，且包含 m 个样本点，则事件 A 出现的概率记为:

常用计数方法：

1.2.3.1重复组合

从 n 个不同元素中每次取出一个，放回后再取下一个，如此连续取r次所得的组合称为重复组合，此种重复组合数共有：

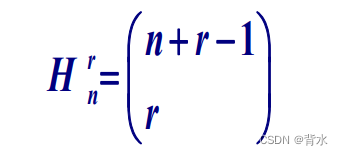
1.2.3.2不全相异元素的排列

在n个元素中，有m类不同元素、每类各有k1 , k2 ,… km 个，将这n个元素作全排列，共有如下种方式：

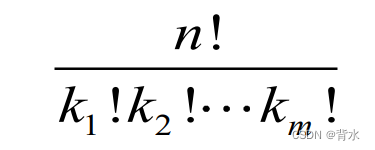
或：

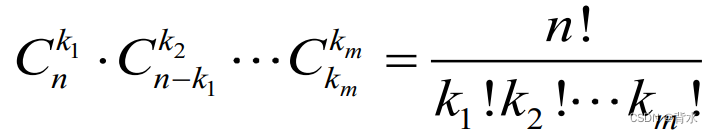
1.2.3.3环排列

从n个不同元素中，选出m个不同的元素排成一个圆圈的排列，共有：

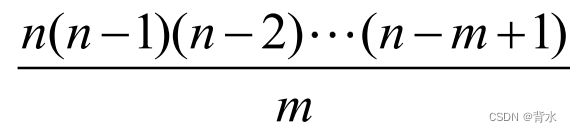
1.2.4古典概型基本模型

1.2.4.1无放回地摸球

设袋中有4 只白球和 2只黑球, 现从袋中无放回地依次摸出2只球,求这2只球都是白球的概率

解答较简单。

1.2.4.2有放回地摸球

设袋中有4只红球和6只黑球,现从袋中有放回地摸球3次,求前2次摸到黑球、第3次摸到红球的概率.

基本事件总数为 $10\times 10\times10=10^{3}$ ,A 所包含基本事件的个数为: $6\times6\times4$

1.2.4.3分球入盒模型(盒子容量无限)

把 4 个球放到 3个盒子中去,求第1、2个盒子中各有两个球的概率, 其中假设每个盒子可放任意多个球.

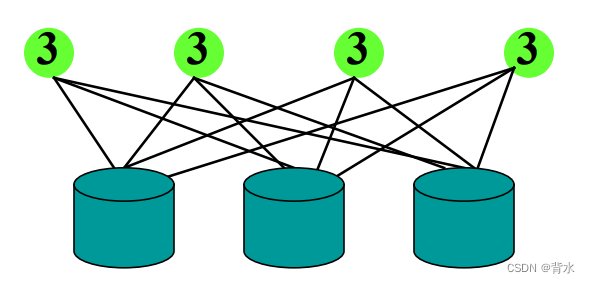
4个球放到3个盒子的所有放法 3*3*3*3=3^4

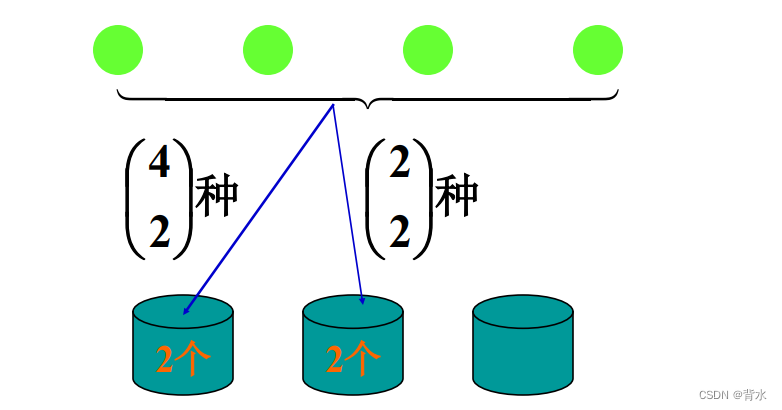
因此第1、2个盒子中各有两个球的概率为:

1.2.4.4分球入盒模型(每个盒子只能放一个球)

把4个球放到10个盒子中去,每个盒子只能放一个球, 求第1 至第4个盒子各放一个球的概率.

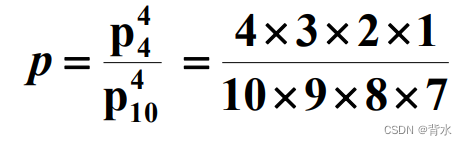
1.2.5基本例题

（1）在7位数的电话号码中,第一位不能为0，求数字0出现3次的概率.

首先确定首位元素有9种选择，再从6各种选出3个位置来放0，接下来3个位置可以放任意数共9^3(注意不能放0了，因为若有一个0，就变成4个0了)

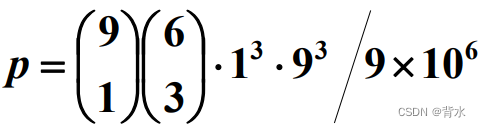
（2）掷3颗均匀骰子,求点数之和为4的概率

点数为4就3种情况，即1\1\2的全排列。

（3）设有 k 个不同的球, 每个球等可能地落入 N 个盒子中（k<=N ）, 设每个盒子容球数无限, 求下列事件的概率.

(3.1)某指定的 k 个盒子中各有一球

(3.2)某指定的一个盒子恰有 m 个球( m<=k)

(3.3)某指定的一个盒子没有球

(3.4)恰有 k 个盒子中各有一球

(3.5)至少有两个球在同一盒子中

反面思考，至少两个的反面就是“0个或1个”在同一个球，这就是3.4的结果，所以用总样本点数减去它就可以了。

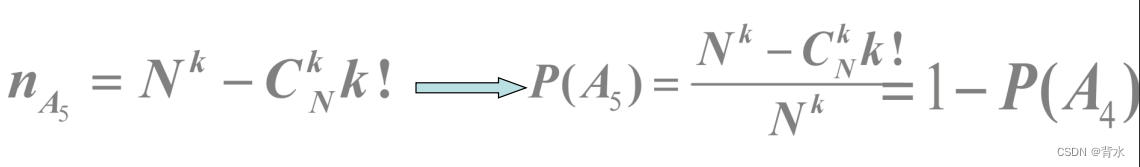
（3.6）生物系二年级有 n 个人，求至少有两人生日相同（设为事件A ) 的概率.

这里也是至少，所以也可以从反面思考。

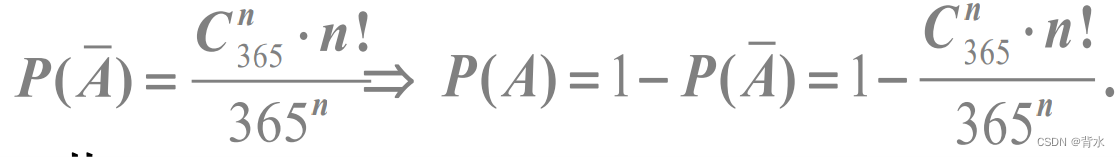
2.概率的性质

2.1可加性

性质1：

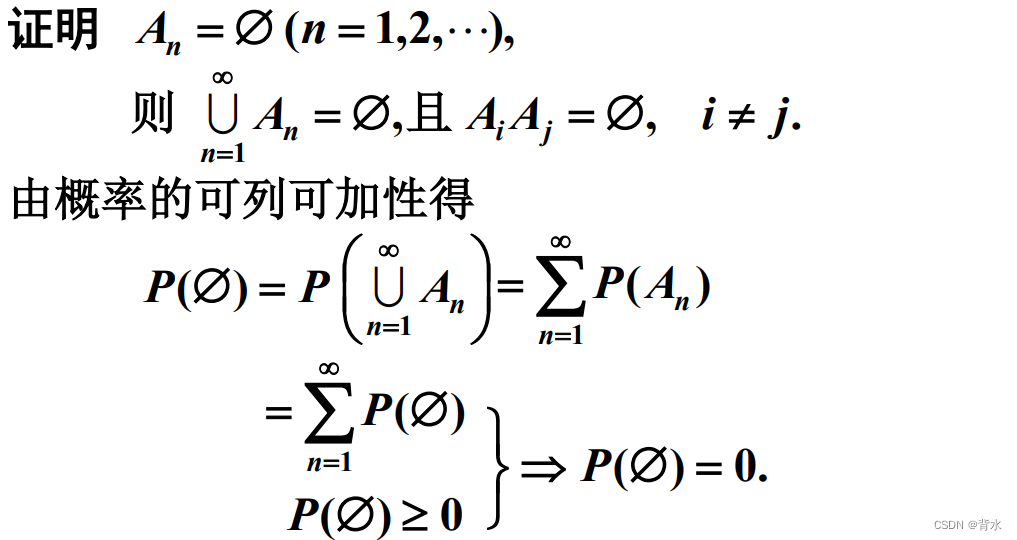
性质2：

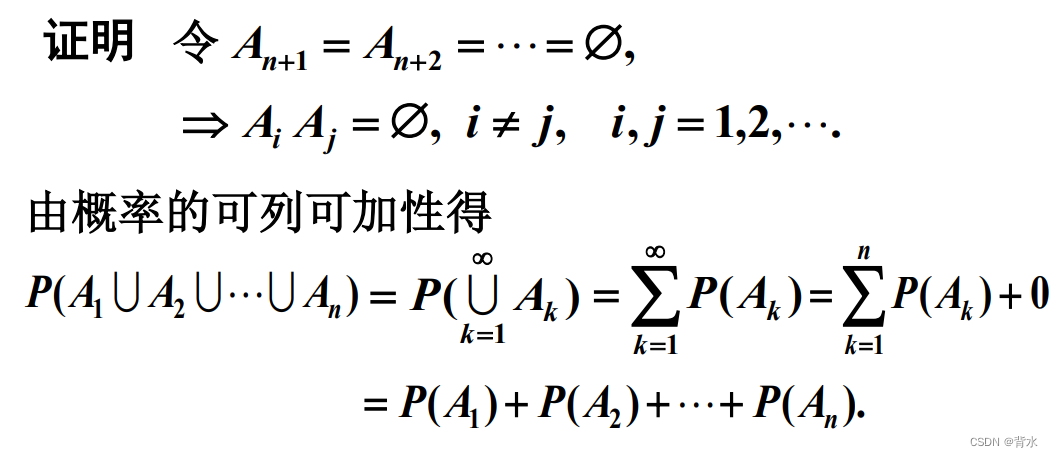
性质3：

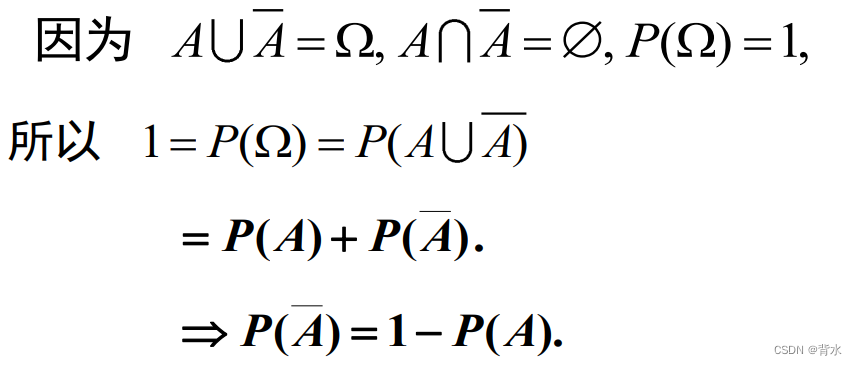
2.2单调性

对任意两个事件A、B， $B\subset A$

P(A-B) = P(A)-P(B)
P(A) >= P(B)

对任意两个事件A、B有

P(A-B) = P(A) -P(AB).

注意：B = AB $\cup$ (~A)B

P(B)=P(AB) + P(~AB)

例题：已知事件A、B的概率分别是1/3 和 1/2，p(AB)=1/8,求p(B~A)的概率。

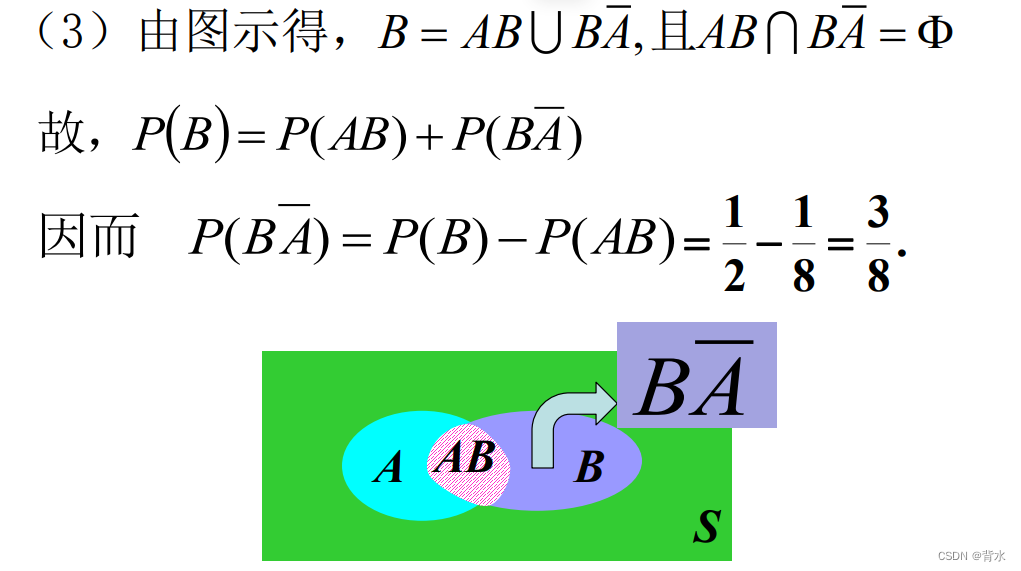
2.3加法公式

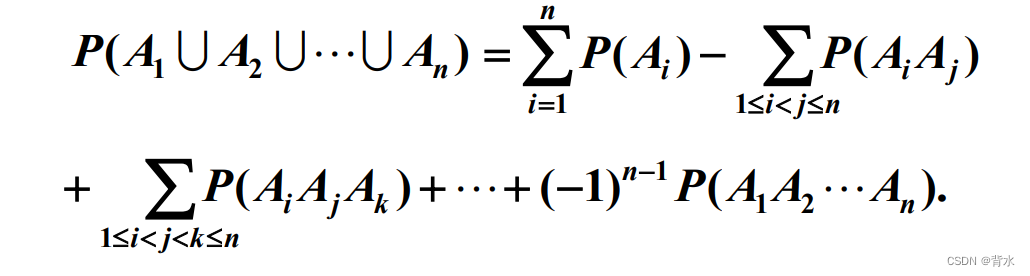
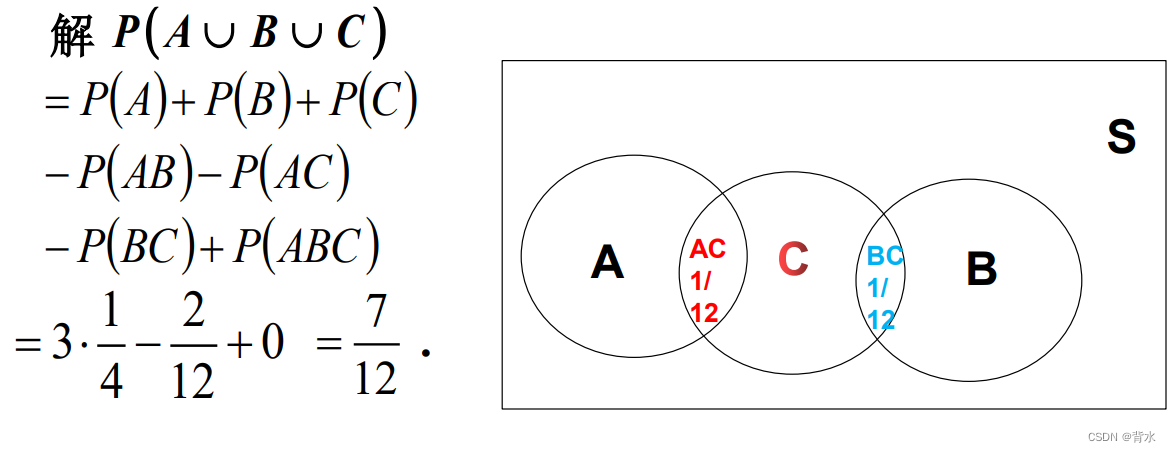
例题1：设A、B、C是三个事件，且p(A)=p(B)=p(C)=1/4，P(AB)=0,P(BC)=P(AC)=1/12,求A、B、C中至少有一个发生的概率。

注意此时还能用1-概率吗？不能，因为P(BC)=P(AC)=1/12这几个概率有交集，并不互斥。

例题2：设A , B满足 P ( A ) = 0.8, P ( B ) = 0.7,在P(A $\cup$ B)为多少的概率下，P(AB)取最大值，最大值是多少？

P(A $\cup$ B)=P(A)+P(B)-P(AB),

P(AB)=P(A)+P(B)-P(A $\cup$ B),=1.5-P(A $\cup$ B),需要P(A $\cup$ B)取最小值时，P(AB)取最大值，注意P(A $\cup$ B)一定大于0.5,因为P(A $\cup$ B)>=max{P(A),P(B)},所以P(A $\cup$ B)=0.8时，P(AB)最大。

3.条件概率

3.1定义和基础

设A、B为两事件, P ( B ) > 0 , 则称P(AB)/P(B)为事件 B 发生的条件下事件 A 发生的条件概率，记为

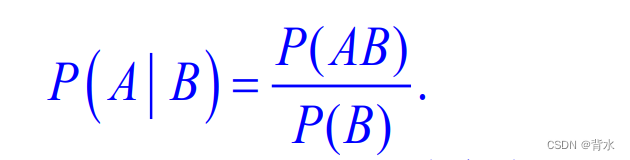
性质:

非负性: P(A|B)>=0

规范性：

可列可加性：

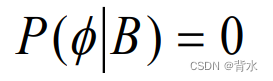
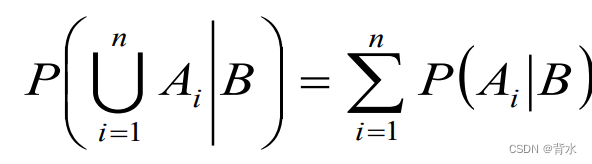
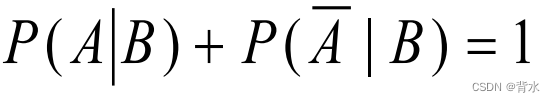
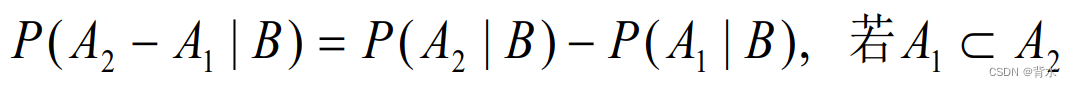
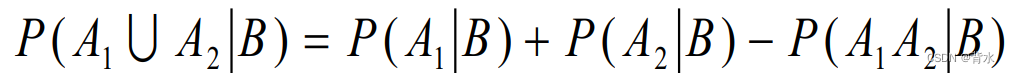
例题：

（1）某种动物由出生算起活20岁以上的概率为 0.8, 活到25岁以上的概率为0.4, 如果现在有一个 20岁的这种动物, 问它能活到25岁以上的概率是多少?

解：设 A 表示“ 能活 20 岁以上 ” 的事件，B 表示 “ 能活 25 岁以上”的事件。

则：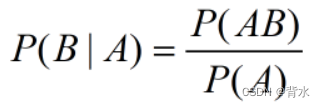

P(AB)=P(B)=0.4;

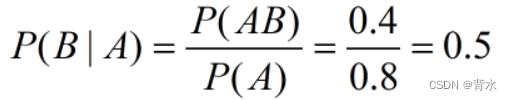
（2）从混有5张假钞的20张百元钞票中任意抽出2 张, 设发现2张钞票中至少有一张钞票是假钞，则2 张都是假钞的概率为：

解：由题知要求在有一张假钞的前提下，另一张也为假钞的概率，设A：其中至少有一张是假钞，B：两张都是假钞。（这里为什么A不能是其中一张是假钞呢？因为如果一张假钞一张真钞，那么两张都是假钞概率为0）

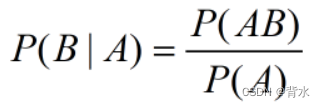
P(AB)=P(B)= $\textrm{C}_{5}^{2}/\textrm{C}_{20}^{2}$

P(A)= $\textrm{C}_{5}^{1}\times \textrm{C}_{19}^{1}/\textrm{C}_{20}^{2}$ ,（注意这个是错误的，因为，有可能两次都选到的是假钞，但是同时选了两遍，比正常要多）。

P(A)= $(\textrm{C}_{5}^{1}\times \textrm{C}_{15}^{1}+\textrm{C}_{5}^{2})/\textrm{C}_{20}^{2}$

3.2乘法公式

设 P(A) > 0, 则有

设 A,B,C 为事件,且 P(AB) > 0, 则有

例题：

盒中装有5个产品, 其中3个一等品，2个二等品, 从中不放回地取产品, 每次1个, 求

（1）取两次，两次都取得一等品的概率;

（2）取两次，第二次取得一等品的概率;

（3）取三次，第三次才取得一等品的概率;

（4）取两次，已知第二次取得一等品，求第一次取得的是二等品的概率。

解：令 $A_{i}$ 为第 i 次取到一等品

(1):

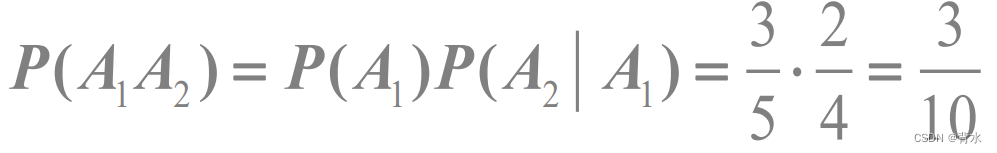
(2):

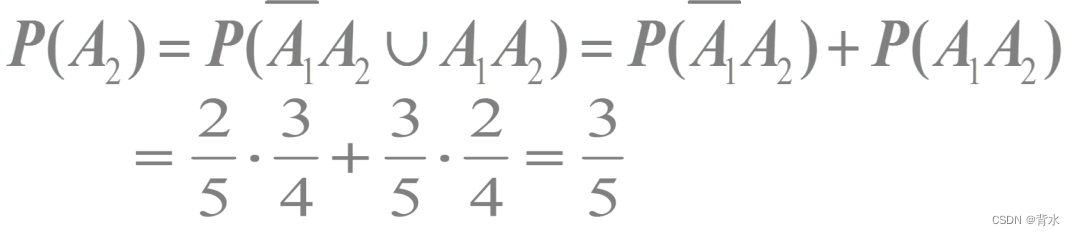
(3):

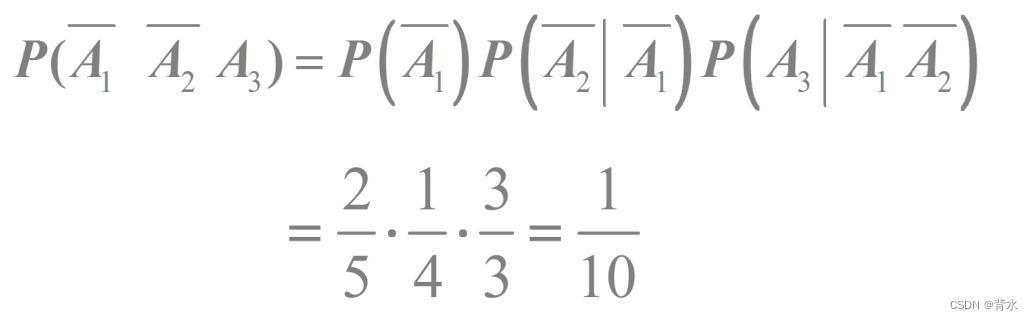
(4):

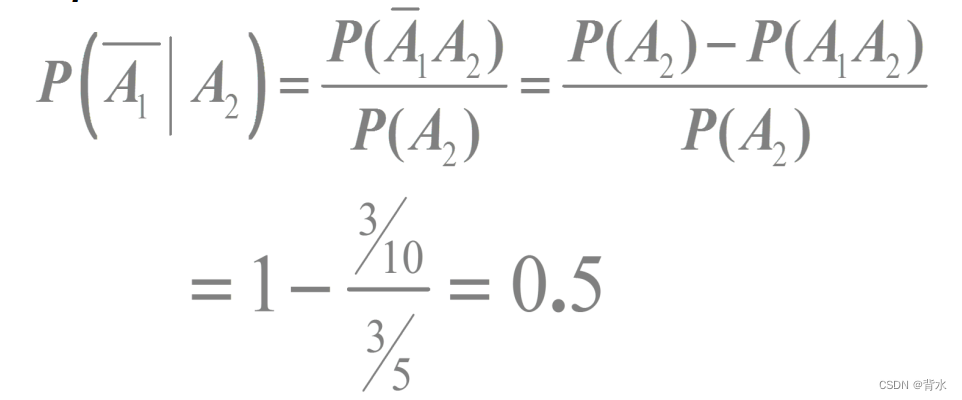
3.3全概率公式

3.3.1样本空间的划分(完备事件组）

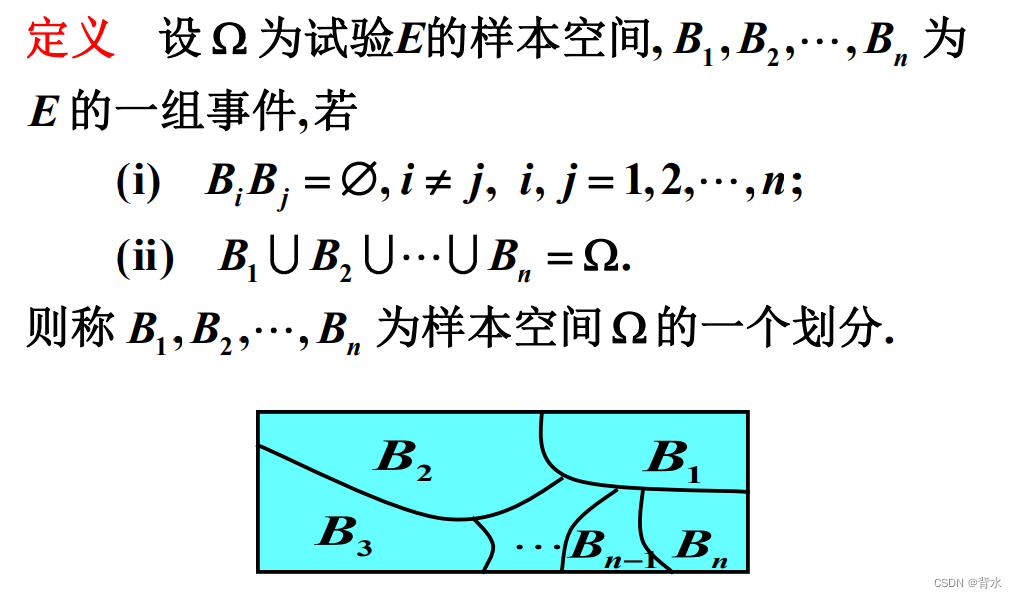
3.3.2

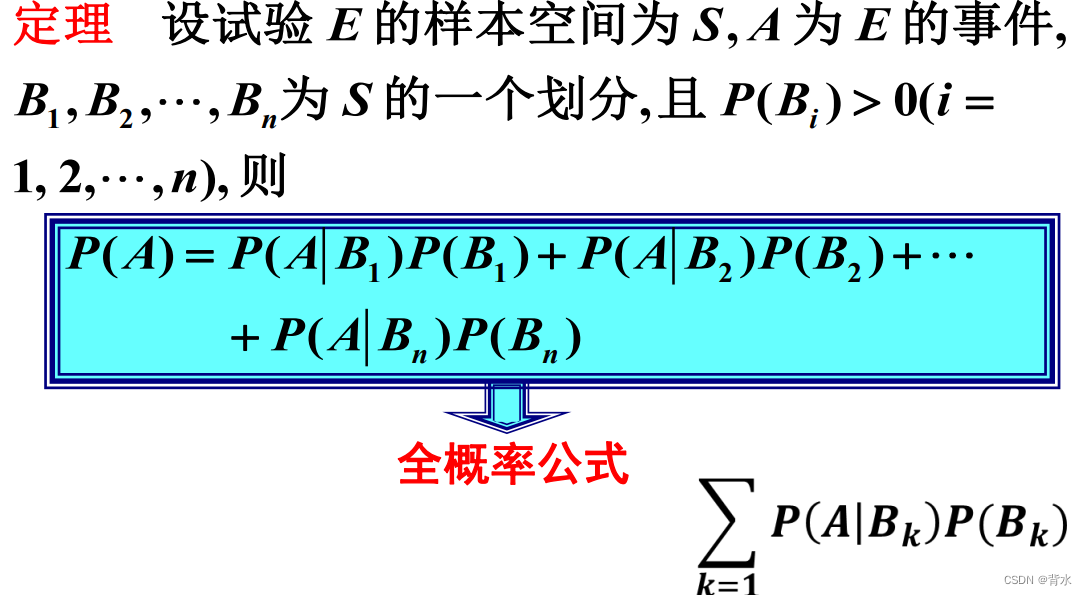
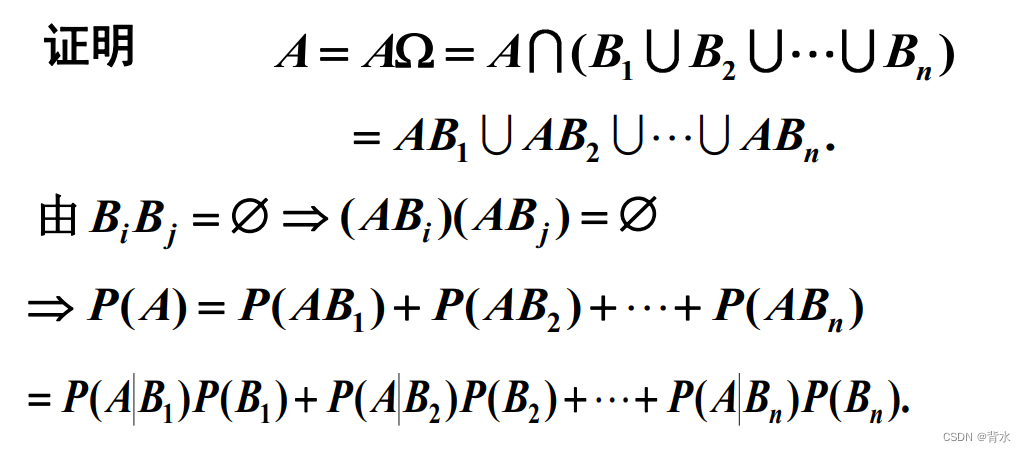
3.4贝叶斯（Bayes)公式

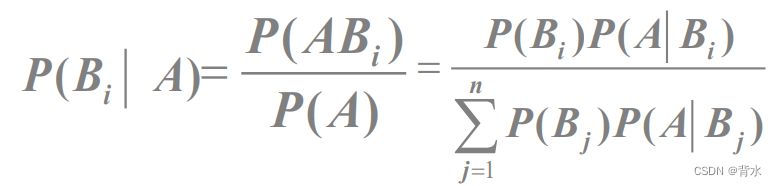
4.独立性

4.1两个事件相互独立

若A、B两个事件独立，那么P(A|B) = P(A)，即

P(AB) = P(A)*P(B)。

性质：（1）若事件 A 、B相互独立，则~A与B、A与~B、~A与~B也相互独立。

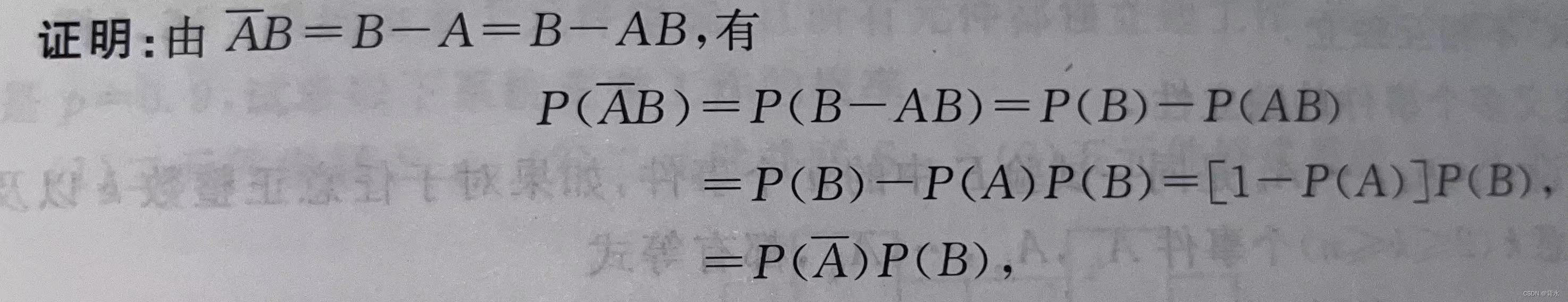
（2）必然事件和不可能事件，与任何事件都是相互独立的

（3）注意：独立只是“概率意义独立”，并不代表二者互斥。

若P(A)>0 、P(B)>0:

A与B独立->	A与B不互斥（A、B相容）
A与B互斥->	A与B不独立

即在两者概率都大于0的情况下，互斥和独立是“负相关”的

4.2多个事件独立

注意：上面定义若取定n=3。则2 <= k <= 3。

k取2时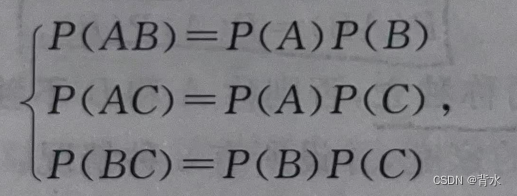：这是从3个(n个)中选出2个进行组合。

k取3时：P(ABC)=P(A)P(B)P(C)。从3个(n个)中选出三个。