算法打卡day14|二叉树篇03|Leetcode 104.二叉树的最大深度、559.n叉树的最大深度、111.二叉树的最小深度、222.完全二叉树的节点个数-编程知识

算法题

Leetcode 104.二叉树的最大深度

题目链接:104.二叉树的最大深度

大佬视频讲解：二叉树的最大深度视频讲解

个人思路

可以使用层序遍历，因为层序遍历会有一个层数的计算，最后计算到的层数就是最大深度；

解法

迭代法

就是层序遍历的模板代码，遍历节点的时候不用添加值，最后返回深度

class Solution {public int maxDepth(TreeNode root) {if(root == null) {return 0;}//层序遍历Deque<TreeNode> deque = new LinkedList<>();deque.offer(root);int depth = 0;while (!deque.isEmpty()) {int size = deque.size();depth++;//计算深度for (int i = 0; i < size; i++) {TreeNode node = deque.poll();if (node.left != null) {deque.offer(node.left);}if (node.right != null) {deque.offer(node.right);}}}return depth;}
}

时间复杂度:O(n)；（遍历整棵树）

空间复杂度:O(n);（使用一个列表）

递归法

递归法也很简单，因为是计算树的最大深度，就把二叉树分为两边，各个计算深度取最大值即可。

本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。力扣上的高度最低是1，也就是从1开始的；

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）

class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;}int leftDepth = maxDepth(root.left);//计算左节点深度int rightDepth = maxDepth(root.right);//计算右节点深度return Math.max(leftDepth, rightDepth) + 1;//加一的原因是还有根节点}
}

时间复杂度:O(n)；（遍历整棵树）

空间复杂度:O(n);（递归树的高度h）

Leetcode 59.n叉树的最大深度

题目链接:59.n叉树的最大深度

个人思路

与上面二叉树的思路差不多，只不过二叉树是遍历左右子树，n叉树就是遍历n各节点

解法

递归法

方法与二叉树最大深度一样，只不过要比较各个节点下的深度

class Solution {/*后序遍历求root节点的高度*/public int maxDepth(Node root) {if (root == null) return 0;int depth = 0;if (root.children != null){for (Node child : root.children){depth = Math.max(depth, maxDepth(child));//各个孩子节点中最高的节点}}return depth + 1; //中节点}  
}

时间复杂度:O(n)；（遍历二叉树）

空间复杂度:O(n);（递归树的高度h

迭代法

与二叉树类似，只修改了孩子节点的遍历放入。

class Solution {//使用层序遍历public int maxDepth(Node root) {if (root == null)   return 0;int depth = 0;Queue<Node> que = new LinkedList<>();que.offer(root);while (!que.isEmpty()){depth ++;//根节点深度加1int len = que.size();//每层元素while (len > 0){Node node = que.poll();//对应二叉树层序遍历的左右节点for (int i = 0; i < node.children.size(); i++)if (node.children.get(i) != null) que.offer(node.children.get(i));len--;}}return depth;//深度}
}

时间复杂度:O(n)；（遍历二叉树）

空间复杂度:O(n);（使用队列）

Leetcode 111.二叉树的最小深度

题目链接:111.二叉树的最小深度

大佬视频讲解:二叉树的最小深度视频讲解

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明:叶子节点是指没有子节点的节点。

个人思路

也可以层序遍历，当第一次遍历到改节点没有左右孩子，那深度就是最小深度。

解法

迭代法

在原来层序遍历的基础上加个判断节点左右孩子是否为空的操作即可；

class Solution {//层序遍历public int minDepth(TreeNode root) {if (root == null) {return 0;}Deque<TreeNode> deque = new LinkedList<>();deque.offer(root);int depth = 0;while (!deque.isEmpty()) {int size = deque.size();depth++;for (int i = 0; i < size; i++) {TreeNode poll = deque.poll();// 当第一次遍历到叶子结点，直接返回depth，因为从上往下遍历，所以该值就是最小值if (poll.left == null && poll.right == null) {return depth;}if (poll.left != null) {deque.offer(poll.left);}if (poll.right != null) {deque.offer(poll.right);}}}return depth;}
}

时间复杂度:O(n)；（遍历整棵树）

空间复杂度:O(n);（使用队列）

递归法

注意在节点左孩子或右孩子为空时的情况，这时深度要加1，看如下代码

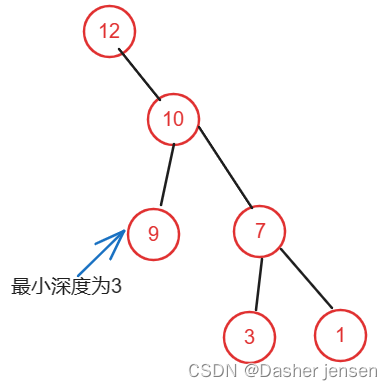
class Solution {public int minDepth(TreeNode root) {1.确定递归函数的参数和返回值if (root == null) {2.确定终止条件return 0;}//3.确定单层递归的逻辑int leftDepth = minDepth(root.left);int rightDepth = minDepth(root.right);if (root.left == null) {return rightDepth + 1;//原因如上图}if (root.right == null) {return leftDepth + 1;}// 左右结点都不为nullreturn Math.min(leftDepth, rightDepth) + 1;}
}

时间复杂度:O(n)；（遍历整棵树）

空间复杂度:O(n);（递归树的高度h）

Leetcode 222.完全二叉树的节点个数

题目链接:222.完全二叉树的节点个数

大佬视频讲解:完全二叉树的节点个数视频讲解

个人思路

将二叉树分为左子树和右子树，递归返回节点个数然后相加

解法

递归法

class Solution {public int countNodes(TreeNode root) {if(root == null) {return 0;}//还有个根节点所以加一return countNodes(root.left) + countNodes(root.right) + 1;}
}

时间复杂度:O(n)；（遍历二叉树）

空间复杂度:O(n);（递归树的高度h）

迭代法

套用层序遍历的模板，只不过不加入节点值，直接计算节点数量

class Solution {public int countNodes(TreeNode root) {if (root == null) return 0;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);int result = 0;while (!queue.isEmpty()) {int size = queue.size();//当层元素个数while (size -- > 0) {TreeNode cur = queue.poll();result++;//遍历一个元素则加1if (cur.left != null) queue.offer(cur.left);if (cur.right != null) queue.offer(cur.right);}}return result;}
}