25考研数据结构复习·3.2队列

队列（Queue）基本概念

  • 定义

    队列（Queue）时只允许在一端进行插入，在另一端删除的线性表。

    特点：先进入队列的元素先出队

    先进先出 First In First Out(FIFO)

    • 重要术语

      队头、队尾、空队列

 

  • 基本操作

    • 创、销

      InitQueue(&Q):初始化队列。构造一个空队列Q。

      DestroyQueue(&Q):销毁队列。销毁并释放队列Q所占用的内存空间。

    • 增、删

      EnQueue(&Q,x):入队，若队列Q未满，则将x加入使之成为新队尾

      DeQueue(&Q,&x):出队，若队列Q非空，则删除对头元素，并用x返回。

      删除队头元素

    • 查：队列的使用场景中大多之访问对头空间。

      GetHead(Q,&x):读队头元素。若队列Q非空，则将对头元素赋值给x。

      不删除队头元素

    • 其他常用操作

      QueueEmpty(Q):判队列空。若队列Q为空返回true，否则返回false

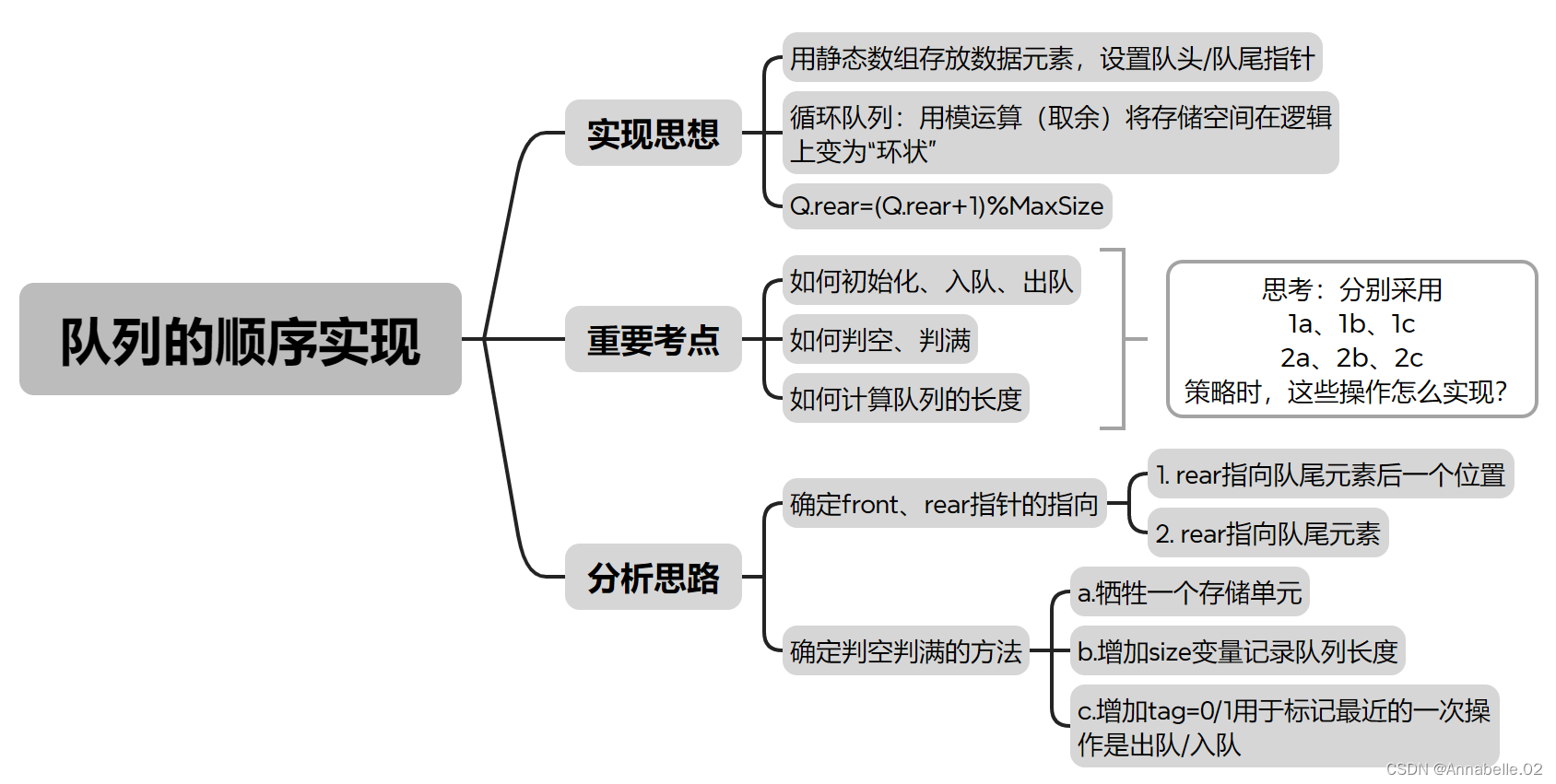
队列的顺序实现

  • 用顺序存储实现队列

#define MaxSize 10       //定义队列中元素的最大个数
typedef struct{//静态数组：连续的存储空间，大小MaxSize*sizeof(ElemType)ElemType data[MaxSize]; //静态数组存放队列中元素int front,rear;               //队头指针和队尾指针
}SqQueue;                void testQueue(){SqQueue Q;  //声明一个队列（顺序存储）//……后续操作……
}

 

  • 基本操作

    • 创（初始化）

      #define MaxSize 10       //定义队列中元素的最大个数
typedef struct{ElemType data[MaxSize] //静态数组存放队列中元素int front,rear;               //队头指针和队尾指针
}SqQueue;                //初始化队列
void InitQueue(SqQueue &Q){//初始时 队头、队尾指针指向0Q.rear = Q.front = 0;
}void testQueue(){    //声明一个队列（顺序存储）SqQueue Q;  InitQueue(Q);//……后续操作……
}//判断队列是否为空
bool QueueEmpty(SqQueue Q){if(Q.rear==Q.front)  //对空条件return true;elsereturn false;
}

    • 增（入队）只能从队尾入队

      #define MaxSize 10       //定义队列中元素的最大个数
typedef struct{ElemType data[MaxSize] //静态数组存放队列中元素int front,rear;               //队头指针和队尾指针
}SqQueue;                //判断队列是否为空
bool QueueEmpty(SqQueue Q){if(Q.rear==Q.front)  //对空条件return true;elsereturn false;
}//入队
bool EnEmpty(SqQueue &Q,ElemType x){if((Q.rear+1)%MaxSize==Q.front)  return false;  //队满则报错Q.data[Q.rear] = x;//将新元素插入队尾Q.rear = (Q.rear + 1)%MaxSize;//队尾指针加1取模return true;
}

      {0,1,2,……,MaxSize-1}将存储空间在逻辑上变成了“环状”——循环队列

      队列已满的条件：队尾指针的再下一个位置是对头，即(Q.rear+1)%MaxSize==Q.front

    • 💭 队列元素个数：(rear+MaxSize-front)%MaxSize

    • ❔ 不浪费一个存储单元 → 增设一个size数据成员

      #define MaxSize 10       //定义队列中元素的最大个数
typedef struct{ElemType data[MaxSize] //静态数组存放队列中元素int front,rear;               //队头指针和队尾指针int size;            //队列当前长度
}SqQueue;

      ❔ 不浪费一个存储单元 → 增设一个tag数据成员

      #define MaxSize 10       //定义队列中元素的最大个数
typedef struct{ElemType data[MaxSize] //静态数组存放队列中元素int front,rear;               //队头指针和队尾指针int tag;            //最近进行的是删除/插入//每次删除操作成功时，都令tag=0;//每次插入操作成功时，都令tag=1;
}SqQueue;

    • 删（出队）只能从对头元素出队

      //出队
bool DeQueue(SqQueue &Q,ElemType &x){if(Q.rear+1==Q.front)  return false;  //队满则报错x = Q.data[Q.front];Q.front = (Q.front + 1)%MaxSize;//队头指针后移return true;
}

    • 查（获取队头元素）

      //获得对头元素的值，用x返回
bool GetHead(SqQueue Q,ElemType &x){if(Q.rear==Q.front)  return false;  //队空则报错x = Q.data[Q.front];return true;
}

  • 其他出题方式

    🐻‍❄️ 队尾指针rear指向队尾元素
    入队操作：
Q.rear = (Q.rear + 1)%MaxSize;
Q.data[Q.rear] = x;
 初始化：

        让front指向0的位置；让rear指向n-1的位置

判空：

        (Q.rear+1)%MaxSize=Q.front

判满：

        (Q.rear+1)%MaxSize=Q.front ❌

        方案一：牺牲一个存储单元（头指针再尾指针后两个位置）

        方案二：增加辅助变量（size/tag）

总结：

 

队列链式实现

  • 定义

    typedef struct LinkNode{     //链式队列结点ElemType data;struct LinkNode *next;               
}LinkNode;                typedef struct{  //链式队列LinkNode *front,*rear;  //队列的队头和队尾指针
}LinkQueue;

链队列——链式存储实现的队列

  • 带头结点

 

 初始化

typedef struct LinkNode{     ElemType data;struct LinkNode *next;               
}LinkNode;                typedef struct{  LinkNode *front,*rear;  
}LinkQueue;//初始化队列
void InitQueue(LinkQueue &Q){//初始时 front rear都指向头结点Q.front=Q.rear=(LinkNode*)malloc(sizeof(LinkNode));Q.front->next=NULL;
}void testLinkQueue(){LinkQueue Q;  //声明一个队列InitQueue(Q);  //初始化队列//……后续操作……
}//判断队列是否为空
bool IsEmpty(LinkQueue Q){if(Q.front == Q.rear)return true;elsereturn false;
}

 

 

 入队

//新元素入队
void EnQueue(LinkQueue &Q,ElemType x){LinkNode *s=(LinkNode *)malloc(sizeof(LinkNode));s->data=x;s->next=NULL;Q.rear->next=s; //新结点插入到rear之后Q.rear=s;  //修改表尾指针
}

 出队

//新元素出队
void DeQueue(LinkQueue &Q,ElemType &x){if(Q.front == Q.rear)return false;    //空队LinkNode *p=Q.front->next;x=p->data;        //用变量x返回队头元素Q.front->next=p->next;//修改头结点的next指针if(Q.rear==p)      //此次时最后一个结点出队Q.rear=Q.front;  //修改rear指针free(p);   //释放结点空间return true;
}

 不带头结点

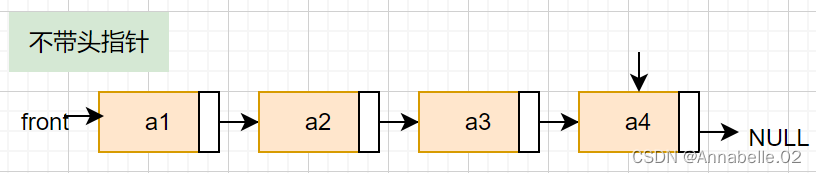
 初始化

//初始化队列
void InitQueue(LinkQueue &Q){//初始时 front rear都指向NULLQ.front=NULL;Q.rear=NULL;
}//判断队列是否为空
bool IsEmpty(LinkQueue Q){if(Q.front == NULL)return true;elsereturn false;
}

 入队

//新元素入队
void EnQueue(LinkQueue &Q,ElemType x){LinkNode *s=(LinkNode *)malloc(sizeof(LinkNode));s->data=x;s->next=NULL;//不带头结点的队列，第一个元素入队时需要特别处理if(Q.front ==NULL){  //在空队列中插入第一个元素Q.front = s;    //修改队头队尾指针Q.rear = s;  }else{Q.rear->next=s; //新结点插入到rear之后Q.rear=s;  //修改rear指针}
}

 出队

//新元素出队
void DeQueue(LinkQueue &Q,ElemType &x){if(Q.front ==NULL)return false;    //空队LinkNode *p=Q.front;  //p指向此次出队的结点x=p->data;        //用变量x返回队头元素Q.front=p->next;//修改front指针if(Q.rear==p)      //此次时最后一个结点出队Q.front=NULL;  //front指向NULLQ.rear=NULL;   //rear指向NULLfree(p);   //释放结点空间return true;
}

 🙌 链式存储——一般不对队满，除非内存不足

双端队列

栈：只允许从一端插入和删除的线性表

队列：只允许从一端插入，另一端删除的线性表

双端队列：允许从两端插入、两端删除的线性表

        输入受限的双端队列：只允许一端插入、两端删除的线性表

        输出受限的双端队列：只允许两端插入、一端删除的线性表

  • 考点：判断输出序列合法性

    若数据元素输入序列为1/2/3/4，则哪些输出序列是合法的？哪些是非法的？

    • 合法

      • 栈

        1/2/3/4；1/2/4/3；1/3/2/4；1/3/4/2；1/4/3/2；

        2/1/3/4；2/1/4/3；2/3/1/4；2/3/4/1；2/4/3/1；

        3/2/1/4；3/2/4/1；3/4/2/1

        4/3/2/1；

        14种合法出栈序列 

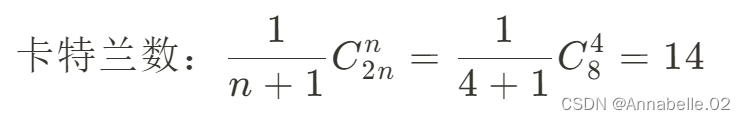
      • 输入受限的双端队列（栈中合法的序列，双端队列中一定也合法）

        在栈中非法在该方法下合法：

        1/4/2/3；2/4/1/3；3/1/2/4；3/1/4/2；3/4/1/2；4/1/2/3；4/1/3/2；4/3/1/2

      • 输出受限的双端队列（栈中合法的序列，双端队列中一定也合法）

        • 在栈中非法在该方法下合法：

          1/4/2/3；2/4/1/3；3/1/2/4；3/1/4/2；3/4/1/2；4/1/2/3；4/2/1/3；4/3/1/2

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/541046.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

AIX上安装gcc和g++

AIX上安装gcc和g++

AIX的iso镜像中没有gcc的软件包，需要我们自己下载，我们可以在 Index of /download/rpmdb/deplists/aix72 下载对应gcc和g版本的依赖文件deps 我们使用的是4.9.4版本的软件包 我们首先安装gcc，在http://www.oss4aix.org/download/everythi…
阅读更多...
天锐绿盾｜公司办公透明加密系统，文件数据 \ 资料防泄密软件

天锐绿盾｜公司办公透明加密系统，文件数据 \ 资料防泄密软件

#防止核心文件、文档、图纸、源代码、音视频等数据资料泄漏，外泄# 天锐绿盾作为一款专业的公司办公透明加密系统，专注于解决企业文件数据与资料的安全保密问题，通过先进的加密技术和全面的安全管理体系，确保企业核心信息资产在日…
阅读更多...
【C++设计模式】策略模式

【C++设计模式】策略模式

文章目录 前言一、策略模式是什么？二、策略模式的实现原理三、UML图四、代码实现总结 前言 策略模式是一种行为设计模式，它允许在运行时选择算法的行为。通过将每个算法封装到具有共同接口的独立类中，客户端可以在不改变自身代码的情况下选择…
阅读更多...
修改 MySQL update_time 默认值的坑

修改 MySQL update_time 默认值的坑

由于按规范需要对 update_time 字段需要对它做默认值的设置 现在有一个原始的表是这样的 CREATE TABLE test_up (id bigint(20) unsigned NOT NULL AUTO_INCREMENT COMMENT 主键id,update_time datetime default null COMMENT 操作时间,PRIMARY KEY (id) ) ENGINEInnoDB DEF…
阅读更多...
Leet code 1658 将x减到0的最小操作数

Leet code 1658 将x减到0的最小操作数

解题思路：滑动窗口 主要思想：正难逆简 题目需要左找一个数 右找一个数 我们不如直接找中间最长的一连串子数让这串子树和为 数组子树和减去X 找不到就返回 -1 滑动窗口双指针从左端出发，进行 进窗口 判断 出窗口 更新结果四个步骤 代码…
阅读更多...
使用API有效率地管理Dynadot域名，使用API设置域名隐私保护

使用API有效率地管理Dynadot域名，使用API设置域名隐私保护

关于Dynadot Dynadot是通过ICANN认证的域名注册商，自2002年成立以来，服务于全球108个国家和地区的客户，为数以万计的客户提供简洁，优惠，安全的域名注册以及管理服务。 Dynadot平台操作教程索引（包括域名邮…
阅读更多...
ChatGPT 实操指南(断人财路版)

ChatGPT 实操指南(断人财路版)

前言 ChatGPT 的横空出世，让很多人焦虑不已，不过，你完全不需要为此焦虑，因为比 AI 更强大永远是驾驭 AI 为自己所用的人类。 而且 GPT 远没有各大商家炒作的那么玄乎 ，它应用逻辑也非常简单，你完全没必要…
阅读更多...
前端提高性能——使用Intersection Observer API对图片视频进行懒加载

前端提高性能——使用Intersection Observer API对图片视频进行懒加载

前言 最近做了一个项目是类似于商城的&#xff0c;需要放很多图片&#xff0c;在用户选择一页五十条时&#xff0c;页面加载速度会比较慢。为了提高性能&#xff0c;选择用Intersection Observer API 实现图片懒加载。 实现步骤 一、html代码&#xff1a; <img class&qu…
阅读更多...
import postcssPxToViewport8Plugin from ‘postcss-px-to-viewport-8-plugin‘；

import postcssPxToViewport8Plugin from ‘postcss-px-to-viewport-8-plugin‘；

npm 命令行&#xff1a; npm i postcssPxToViewport8Plugin package.json插件的版本&#xff1a; 重点&#xff1a;引入插件的两种方式 postcss-px2rem-exclude配置 postcss.config.js无效 为什么引入插件不生效&#xff1f; 发现没有效果&#xff0c;然后然后百度网上资料发现…
阅读更多...
立体声骨传导蓝牙耳机哪个好？骨传导蓝牙耳机选购避坑的几大要点

立体声骨传导蓝牙耳机哪个好？骨传导蓝牙耳机选购避坑的几大要点

最近骨传导蓝牙耳机以其创新的设计成为众多消费者的热门话题。这类耳机可以让用户在听音乐的同时清晰地听到周围环境的声音&#xff0c;这样的设计使得骨传导蓝牙耳机在过去两年中迅速赢得了用户的青睐。随着市场的不断扩大&#xff0c;各式各样的骨传导蓝牙耳机纷纷涌现&#…
阅读更多...
监听抖音直播间的评论并实现存储

监听抖音直播间的评论并实现存储

监听抖音直播间评论&#xff0c;主要是动态监听dom元素的变化&#xff0c;如果评论是图片类型的&#xff0c;获取alt的值 主要采用的是MutationObserver&#xff1a;https://developer.mozilla.org/zh-CN/docs/Web/API/MutationObserver index.js如下所示:function getPL() {…
阅读更多...
idea项目mapper.xml中的SQL语句黄色下划线去除

idea项目mapper.xml中的SQL语句黄色下划线去除

问题描述 当我们使用idea开发java项目时&#xff0c;经常会与数据库打交道&#xff0c;一般在使用mybatis的时候需要写一大堆的mapper.xml以及SQL语句&#xff0c;每当写完SQL语句的时候总是有黄色下划线&#xff0c;看着很不舒服。 解决方案&#xff1a; 修改idea的配置 Edi…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023