【Leetcode每日一题】递归 - 反转链表（难度⭐）（35）-编程知识

【Leetcode每日一题】递归 - 反转链表（难度⭐）（35）

1. 题目解析

题目链接：206. 反转链表

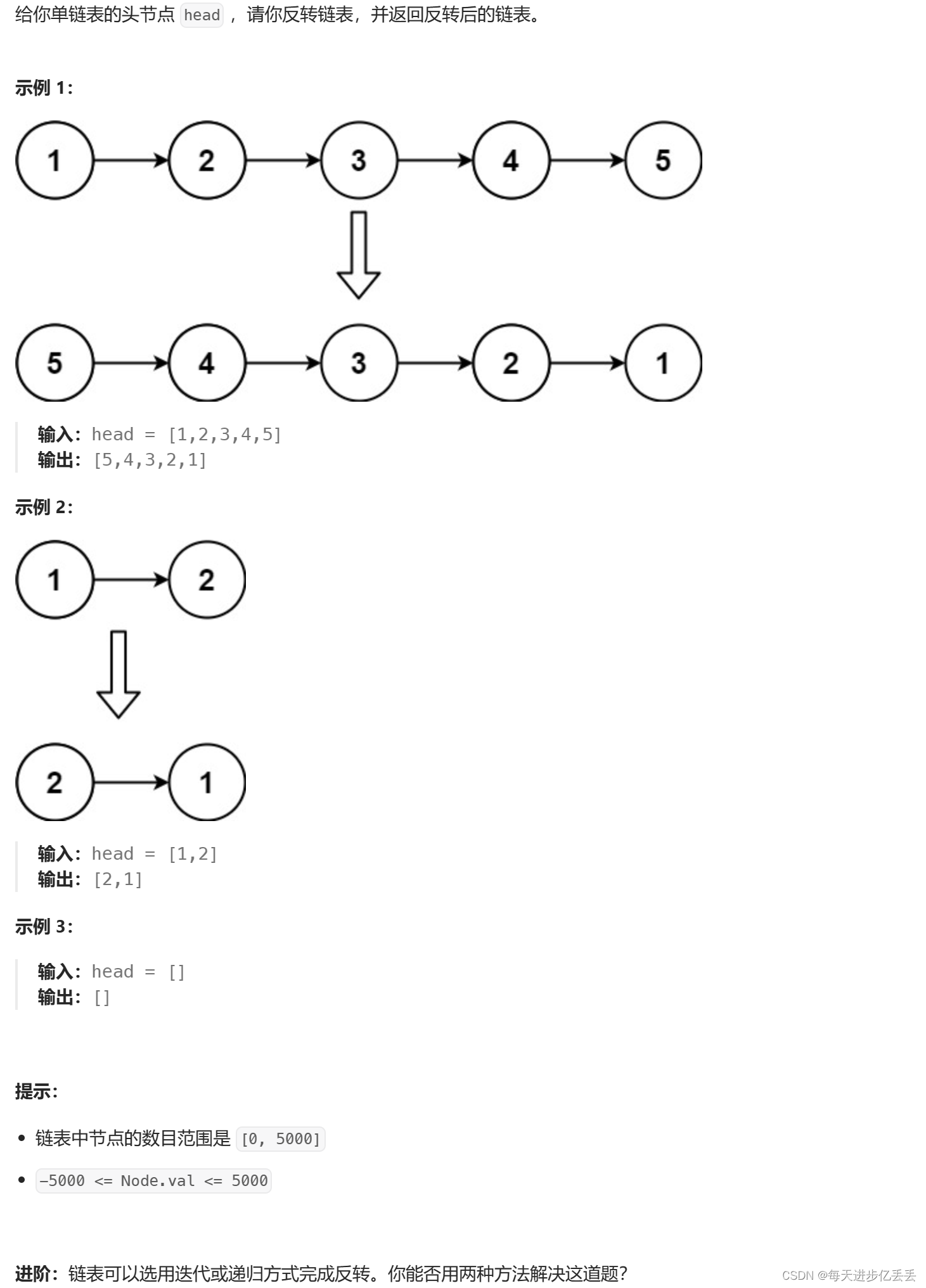
这个问题的理解其实相当简单，只需看一下示例，基本就能明白其含义了。

2.算法原理

一、递归函数的核心任务

递归函数的主要职责是接受一个链表的头指针，并返回该链表逆序后的新头结点。递归的核心思想在于将问题分解为更小的子问题，并通过解决这些子问题来最终解决整个问题。

二、函数体的实现步骤

递归调用：首先，函数会递归地调用自身，以逆序当前结点之后的链表部分。这意味着函数会不断地深入链表的尾部，直到达到递归的出口条件。
处理当前结点：在递归返回后，我们已经得到了逆序后的链表部分。此时，我们需要将当前的结点添加到这个逆序链表的末尾。由于链表是单向的，我们需要小心地处理指针的指向，确保新添加的结点能够正确地链接到逆序链表上。

三、递归出口条件

递归函数需要有一个明确的出口条件，以避免无限递归。在这个问题中，出口条件就是当前结点为空（即链表已经遍历到末尾）或者当前链表只有一个结点。在这两种情况下，不需要进行逆序操作，函数直接返回当前结点即可。

四、注意事项

在处理链表相关的问题时，务必注意指针的操作。链表是通过指针来连接各个结点的，因此指针的指向必须正确无误。为了更好地理解指针的操作和链表的结构，建议在解决问题时画图辅助思考。通过图形化的方式，可以更直观地理解链表的逆序过程，以及指针在逆序过程中的变化。

小tips

这个递归算法的思路是通过不断地将问题分解为更小的子问题，并利用递归调用解决这些子问题，最终完成整个链表的逆序操作。在实现过程中，需要注意指针的正确操作，并确保递归有明确的出口条件。通过画图辅助思考，可以更好地理解链表的结构和指针的操作过程。

3.代码编写

1.递归写法

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution 
{
public:ListNode* reverseList(ListNode* head) {if(head == nullptr || head->next == nullptr) return head;ListNode *h = reverseList(head->next);head->next->next = head;head->next = nullptr;return h;}
};

2.迭代写法

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution 
{
public:ListNode* reverseList(ListNode* head) {if(head == nullptr) {return nullptr;}ListNode *pre = nullptr;ListNode *cur = head;ListNode *next = nullptr;while(cur->next != nullptr) {next = cur->next;cur->next = pre;pre = cur;cur = next;}cur->next = pre;return cur;}
};