本系列是算法通关手册LeeCode的学习笔记
算法通关手册(LeetCode) | 算法通关手册(LeetCode) (itcharge.cn)
目录
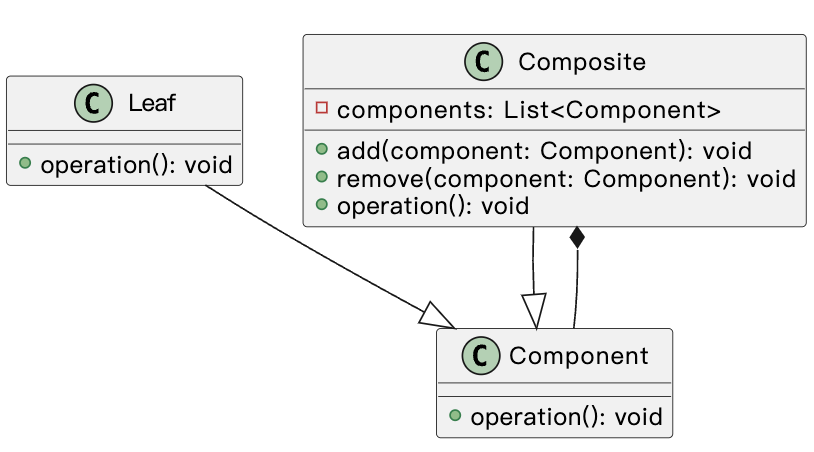
一,二叉搜索树(Binary Search Tree)
二叉搜索树的查找
二叉搜索树的插入
二叉搜索树的创建
二叉搜索树的删除
二,线段树(Segment Tree):
线段树的构建
线段树的单点更新
线段树的区间查询
线段树的区间更新
一,二叉搜索树(Binary Search Tree)
如果任意节点的左子树不为空,则左子树上所有节点的值均小于它的根节点的值;
如果任意节点的右子树不为空,则右子树上所有结点的值均大于它的根节点的值;
任意节点的左子树、右子树均为二叉搜索树;
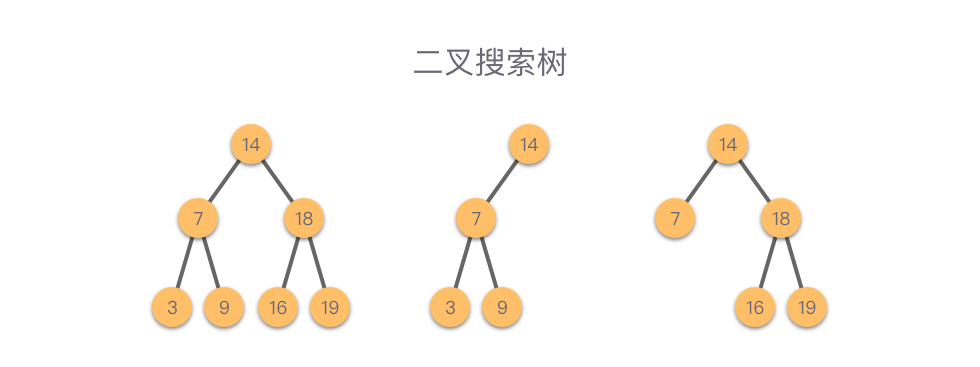
根据二叉搜索树,即左子树的节点值 < 根节点值 < 右子树的节点值 这一特性,如果以中序遍历的方式遍历整个二叉树,则会得到一个递增序列。
二叉搜索树的查找
在二叉搜索树中查找值为 val 的节点:
如果二叉搜索树为空,则返回 None;
如果二叉搜索树不为空,则将要查找的值 val 与 root.val 比较:
如果 val == root.val ,则查找成功,返回找到的节点;
如果 val < root.val ,则递归查找左子树;
如果 val > root.val ,则递归查找右子树。
class TreeNode:def __init__(self, val = 0, left = None, right = None):self.val = valself.left = leftself.right = rightclass Solution:def searchBST(self, root: TreeNode, val: int):if not root:return Noneif val == root.val:return rootelif val < root.val:return self.searchBST(root.left, val)else:return self.searchBST(root.right, val)二叉搜索树的插入
在二叉搜索树中插入一个值为 val 的节点:
如果二叉搜索树为空,则创建一个值为 val 的节点,并作为根节点;
如果二叉搜索树不为空,则将插入的值 val 与二叉搜索树根节点的值 root.val 比较:
如果 val < root.val ,则递归将值插入左子树;
如果 val > root.val ,则递归将值插入右子树。
PS:二叉搜索树不存在重复节点,否则将违反定义。如果 val 已经存在,则直接返回。
def insertIntoBST(self, root: TreeNode, val: int):if root == None:return TreeNode(val)if val < root.val:root.left = self.insertIntoBST(root.left, val)if val > root.val:root.right = self.insertIntoBST(root.right, val)return root二叉搜索树的创建
根据数组序列中的元素值,建立一棵二叉搜索树:
初始化二叉搜索树为空树;
遍历数组元素,将数组元素 nums[i] 依次插入到二叉搜索树中;
将数组中全部元素值插入到二叉搜索树中后,返回二叉搜索树的根节点。
class TreeNode:def __init__(self, val = 0, left = None, right = None):self.val = valself.left = leftself.right = rightclass Solution:def searchBST(self, root: TreeNode, val: int):if not root:return Noneif val == root.val:return rootelif val < root.val:return self.searchBST(root.left, val)else:return self.searchBST(root.right, val)def buildBST(self, nums):root = TreeNode(nums[0])for num in nums[1:]:self.insertIntoBST(root, num)return root二叉搜索树的删除
在二叉搜素树种删除值为 val 的节点:
删除节点并不困难,难点在于保持删除后的仍然是二叉搜索树,可以分为三种情况
1,被删除节点的左子树为空:
则令其右子树代替被删除节点的位置;
2,被删除节点的右子树为空:
则令其左子树代替被删除节点的位置;
3,被删除节点的左右子树都不为空:
考虑二叉搜索树的特点:中序遍历结果是一个升序排列,那么将被删除节点的中序遍历
前驱或后继替换当前节点即可,这样保证了新树的中序遍历仍为升序。
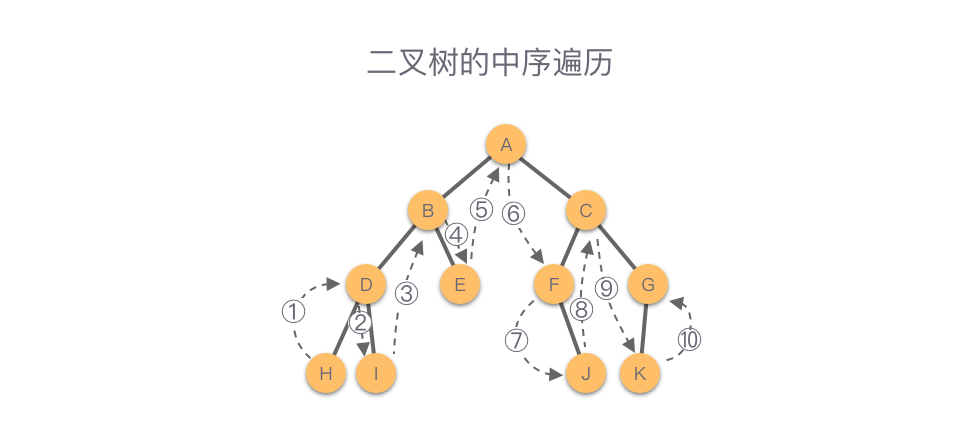
观察 C 节点我们可以发现,中序遍历的前驱是其左子树的最右侧叶子节点,而中序遍历的后继是其右子树最左侧的叶子节点。
如果当前节点为空,则返回当前节点;
如果当前节点的值大于 val,则递归去左子树搜索并删除,因为左子树可能有变化,所以 root.left 也要跟着递归更新;
如果当前节点的值小于 val,则递归去右子树搜索并删除,root.right 也要递归更新;
如果当前节点的值等于 val:
如果当前节点的左子树为空,则删除之后,右子树代替当前节点位置,返回右子树;
如果当前节点的右子树为空,则删除之后,左子树代替当前节点位置,返回左子树;
如果当前节点左右子树后不为空,则将左子树转移到右子树最左侧叶子节点的位置,然
后右子树代替当前节点的位置。
def deleteNode(self, root: TreeNode, val: int):if root == None:return Noneif root.val > val:root.left = self.deleteNode(root.left, val)elif root.val < val:root.right = self.deleteNode(root.right, val)else:if root.left == None and root.right == None:root = Nonereturn rootelif root.left != None and root.right == None:return root.leftelif root.left == None and root.right != None:return root.rightelse:node = root.rightwhile node.left:node = node.leftroot.val = node.val# 删除右子树的最小值root.right = self.deleteNode(root.right, node.val)return root98. 验证二叉搜索树
class Solution:def isValidBST(self, root: Optional[TreeNode]) -> bool:if not root:return Trueans = []def inorder(root):if not root:return inorder(root.left)ans.append(root.val)inorder(root.right)return ansans = inorder(root)for i in range(1, len(ans)):if ans[i] <= ans[i - 1]:return Falsereturn True
173. 二叉搜索树迭代器
class BSTIterator:def __init__(self, root: TreeNode):self.stack = []self.in_order(root)def in_order(self, node):while node:self.stack.append(node)node = node.leftdef next(self) -> int:node = self.stack.pop()if node.right:self.in_order(node.right)return node.valdef hasNext(self) -> bool:return len(self.stack) != 0
用显式栈维护二叉搜索树,要注意节点的访问顺序。
二,线段树(Segment Tree):
一种基于分治思想的二叉树,用于在区间上进行信息统计,它的每一个节点都对应一个区间[left, right],left,right 通常是整数。每一个叶子节点表示了一个单位区间(长度为 1 ),叶子节点对应区间上 left = right。每一个非叶子节点 [left, right] 的左叶子节点都为 [left, (left + right) / 2],右叶子节点表示的区间都为 [(left + right) / 2 + 1, right]。
线段树是一棵平衡二叉树(高度差不超过 1),树上的每个节点维护一个区间。根节点维护的是整个区间,每个节点维护的是父节点区间二等分之后的其中一个子区间。当有 n 个元素时,对区间操作可以在 O(logn) 的时间复杂度内完成。
区间为 [0, 7]的线段树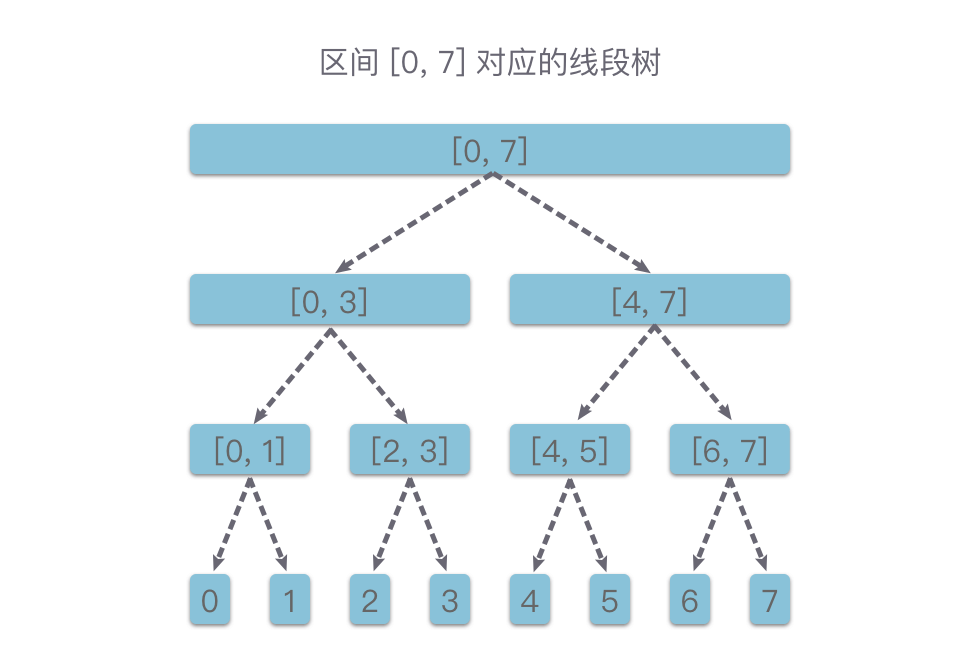
线段树的特点:
线段树的每个节点都代表一个区间;
线段树具有唯一的根节点,代表的区间时整个统计范围;
线段树的每个叶子节点都代表一个长度为 1 的区间[x, x];
对于每个内部节点[left, right],它的左子节点是 [left, mid],右子节点是 [mid + 1, right]。其中 mid = (left + right) / 2。
线段树的构建
由于线段树近乎是完全二叉树,所以使用 顺序存储结构。
我们可以采用与完全二叉树类似的编号方法来对线段树进行编号:
根节点的编号为 0;
如果某二叉树节点(非叶子节点)的下标为 i,那么其左孩子的下标为 2 * i + 1,右孩子
节点的下标为 2 * i + 2;
如果某二叉树节点(非根节点)的下标为 i,那么其父节点的下标为 (i - 1) // 2。
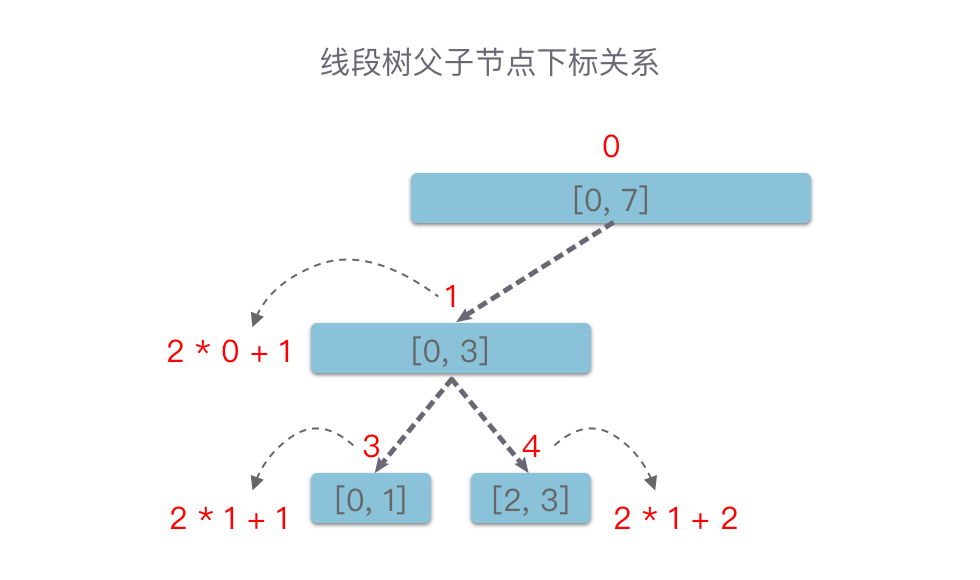
上图可知,下标为 i 节点的子节点下标为 2 * i + 1 和 2 * i + 2,所以线段树适合采用递归的方法来创建:
如果是叶子节点(left = right),则节点的值就是对应位置的元素值;
如果是非叶子节点,则递归创建左右子树;
节点的区间值(区间和、区间最大值、区间最小值)等于该节点左右子节点元素值的对应计算结果。
class SegmentTreeNode:def __init__(self, val = 0):self.left = -1self.right = -1self.val = valself.lazy_tag = Noneclass SegmentTree:def __init__(self, nums, function): # function 根据题目要求确定该节点的值self.size = len(nums)self.tree = [SegmentTreeNode() for _ in range(4 * self.size)]self.nums = numsself.function = functionif self.size > 0:self.__build(0, 0, self.size -1)def __build(self, index, left, right):self.tree[index].left = leftself.tree[index].right = rightif left == right:self.tree[index].val = self.nums[left]returnmid = left + (right - left) // 2 # mid 记录节点存储的区间长度left_index = index * 2 + 1right_index = index * 2 + 2self.__build(left_index, left, mid)self.__build(right_index, mid + 1, right)self.__pushup(index)def __pushup(self, index):left_index = index * 2 + 1right_index = index * 2 + 2# 按照节点值的计算方式,更新当前节点的值# 因为是递归地构造线段树,所以叶子节点已经构造好self.tree[index].val = self.function(self.tree[left_index].val, self.tree[right_index].val)
线段树的单点更新
修改一个元素的值,例如将 nums[ i ] 修改为 val:
如果是叶子节点,满足 left = right,则更新该节点的值;
如果是非叶子节点,则判断应该在左子树还是在右子树中更新;
在对应的子树中更新节点值;
左右子树更新返回之后,向上更新节点的区间值( function 中实现的 区间和、区间最大
值或是区间最小值等)。
def update_point(self, i, val):self.nums[i] = valself.__update_point(i, val, 0, 0, self.size - 1)def __update_point(self, i, val, index, left, right):if self.tree[index].left == self.tree[index].right:self.tree[index].val = valreturnmid = left + (right - left) // 2left_index = index * 2 + 1right_index = index * 2 + 2if i <= mid:self.__update_point(i, val, left_index, left, mid)else:self.__update_point(i, val, right_index, mid + 1, right)self.__pushup(index)线段树的区间查询
查询一个区间为 [q_left, q_right] 的区间值:
如果区间 [q_left, q_right] 完全覆盖了当前节点所在的区间 [left, right] ,即 left >= q_leftt 并且 right <= q_right,则返回该节点的区间值,即该节点的 val;
如果区间 [q_left, q_right] 与当前节点毫无关系,则返回 0;
如果区间 [q_left, q_right] 与当前节点所在区间有交集,则:
如果区间 [q_left, q_right] 与左子树所在区间 [left, mid] 有交集,则在当前节点的左
子树中进行查询,并保存查询结果 res_left;
如果区间 [q_left, q_right] 与右子树所在区间 [mid + 1, right] 有交集,则在当前节
点的右子树中进行查询,并保存查询结果 res_right;
最后返回左右子树元素区间值的聚合计算结果。
def query_interval(self, q_left, q_right):return self.__query_interval(q_left, q_right, 0, 0, self.size - 1)def __query_interval(self, q_left, q_right, index, left, right):if left >= q_left and right <= q_right:return self.tree[index].valif right < q_left or left > q_right:return 0self.__pushdown(index) # 在访问节点时调用mid = left + (right - left) // 2left_index = index * 2 + 1right_index = index * 2 + 2res_left = 0res_right = 0if q_left <= mid:res_left = self.__query_interval(q_left, q_right, left_index, left, mid)if q_right > mid:res_right = self.__query_interval(q_left, q_right, right_index, mid + 1, right)return self.function(res_left, res_right)其中 self.__pushdown() 函数的作用在线段树的区间更新中
线段树的区间更新
对 [q_left, q_right] 区间进行更新,如将 [q_left, q_right] 区间内所有元素更新为 val:
在区间更新操作中,如果某个节点区间P [left, right] 被修改区间 [q_left, q_right] 完全覆盖,则以该节点 P 为根的整棵子树中的节点,都要修改。但是如果后序的查找操作中,没有用到修改后的节点 P 作为候选答案,那么更新以节点 P 为根的子树这一操作就是徒劳的。
因此在节点中
class SegmentTreeNode:def __init__(self, val = 0):self.left = -1self.right = -1self.val = valself.lazy_tag = None最后一行增加了一个【延迟标记】,意为 该区间曾经被修改为 val,但其子节点的值尚未更新。也就是说,将区间节点 P 子节点的更新操作延迟到 在后续操作中递归进入子节点 时再执行。
使用 延迟标记 的区间更新步骤为:
如果区间 [q_left, q_right] 完全覆盖了当前节点所在区间 [left, right],则更新当前节点所在区间的值,并将当前节点的延迟标记为区间值;
如果区间 [q_left, q_right] 与当前节点所在区间毫无关系,则直接返回;
如果区间 [q_left, q_right] 与当前节点所在区间有交集:
如果当前节点使用了【延迟标记】,即延迟标记不为 None,则将当前区间的更新操作应
用到该节点的子节点上,即向下更新;
如果区间 [q_left, q_right] 与左子节点所在区间有交集,则在左子树中更新区间值;
如果区间 [q_left, q_right] 与右子节点所在区间有交集,则在右子树中更新区间值;
左右子树更新返回后,向上更新区间值。
PS:向下更新
更新左子节点和左子节点的 lazy_tag = val;
更新右子节点和右子节点的 lazy_tag = val;
将当前节点的 lazy_tag = None;
def update_interval(self, q_left, q_right, val):self.__update_interval(q_left, q_right, val, 0, 0, self.size - 1)def __update_interval(self, q_left, q_right, val, index, left, right):if left >= q_left and right <= q_right:interval_size = (right - left + 1)self.tree[index].val = interval_size * valself.tree[index].lazy_tag = valreturnif right < q_left or left > q_right:return 0self.__pushdown(index)mid = left + (right - left) // 2left_index = index * 2 + 1right_index = index * 2 + 2if q_left <= mid:self.__update_interval(q_left, q_right, val, left_index, left, mid)if q_right > mid:self.__update_interval(q_left, q_right, val, right_index, mid + 1, right)self.__pushup(index)# 向下更新下标为 index 的节点所在区间的左右子节点的值个 lazy_tagdef __pushdown(self, index):lazy_tag = self.tree[index].lazy_tagif not lazy_tag:returnleft_index = index * + 1right_index = index * 2 + 2self.tree[left_index].lazy_tag = lazy_tagleft_size = self.tree[left_index].right - self.tree[left_index].left + 1self.tree[left_index].val = lazy_tag * left_sizeself.tree[right_index].lazy_tag = lazy_tagright_size = self.tree[right_index].right - self.tree[right_index].left + 1self.tree[right_index].val = lazy_tag * right_sizeself.tree[index].lazy_tag = None算法通关手册(LeetCode) | 算法通关手册(LeetCode)
原文内容在这里,如有侵权,请联系我删除。