题目描述
你所在城市的街道好像一个棋盘,有 a 条南北方向的街道和 b 条东西方向的街道。南北方向的 a 条街道从西到东依次编号为 1 到 a,而东西方向的 b 条街道从南到北依次编号为 1 到 b,南北方向的街道 i 和东西方向的街道 j 的交点记为 (i,j)。
你住在 (1,1) 处,而学校在 (a,b) 处,你骑自行车去上学,自行车只能沿着街道走,而且为了缩短时间只允许沿着向东和北的方向行驶。
现在有 N 个交叉路口在施工 (X1,Y1)、(X2,Y2)……,(Xn,Yn),这些路口是不能通车的。
问你上学一共有多少走法?
输入格式
第一行包含两个整数 a 和 b,并且满足 1≤a,b≤16。
第二行包含一个整数 N,表示有 N 个路口在维修 (1≤N≤40)。
接下来 N 行,每行两个整数Xi,Yi,描述路口的位置。
输出格式
输出一个整数表示从(1,1) 到 (a,b) 的行车路线总数。
输入输出样例
输入 #1
5 4 3 2 2 2 3 4 2
输出 #1
5
说明/提示
【样例解释】
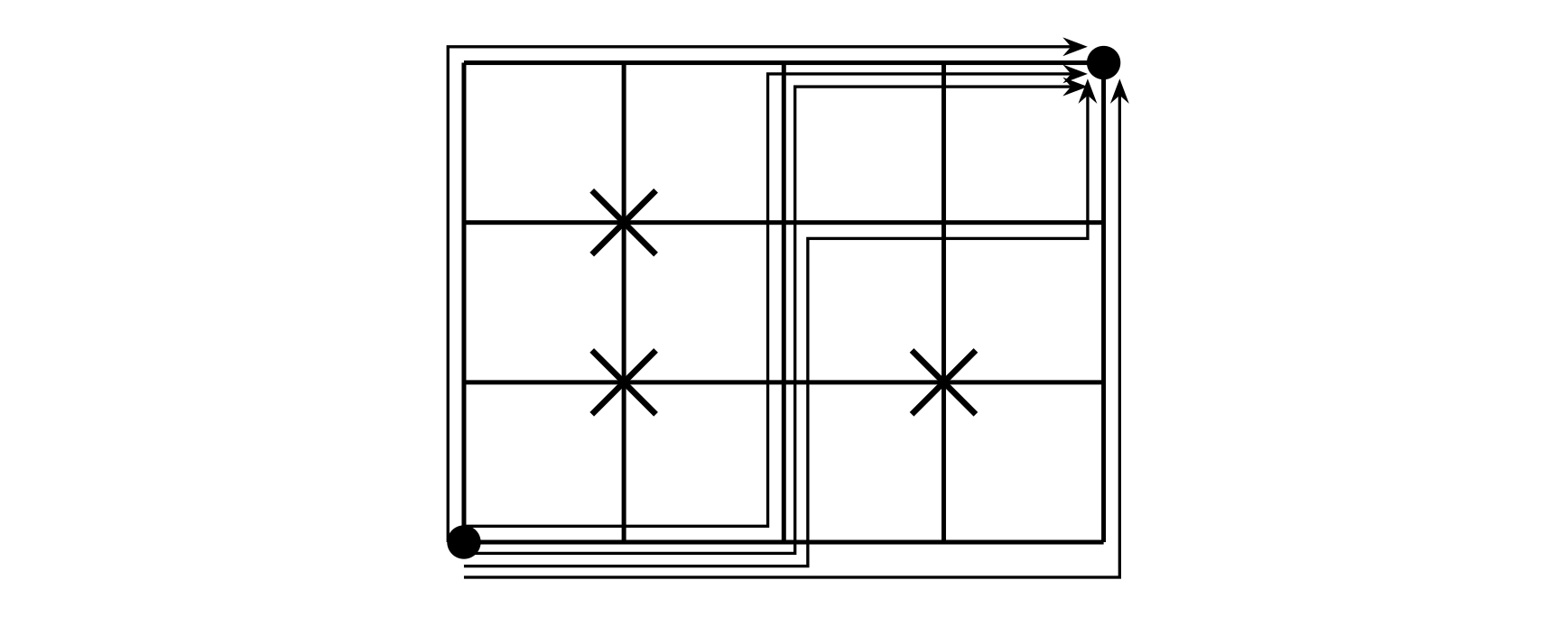
思路
用dfs(),模拟上学的路线,若是施工地点则return.
AC代码
#include<bits/stdc++.h>using namespace std;int a,b,t,x,y,tot=0;
int s[20][20];void dfs(int xx,int yy)
{if(xx==a && yy==b){tot++;return;}if(s[xx][yy+1]==0 && yy+1<=b) dfs(xx,yy+1);if(s[xx+1][yy]==0 && xx+1<=a) dfs(xx+1,yy);
}
int main(){//freopen("x.in","r",stdin);//freopen("x.out","w",stdout);cin>>a>>b;cin>>t;while(t--){cin>>x>>y;s[x][y]=1;}dfs(1,1);cout<<tot<<endl;return 0;
}