当我们初步了解二叉树后
我们就可以进一步去深入学习二叉树了
1.链式二叉树的遍历
这里我们先去定义链式二叉树的结构
分为两个指针
一左一右
他们分别指向左子树和右子树
typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinartTreeNode* left;struct BinartTreeNode* right;
}TreeNode;

左右子树的节点又可以细分为:根,左子树,右子树
图中的1节点就是根,2和3则是左子树,456则是右子树
1.1二叉树的前序,中序,后序遍历
前序遍历、中序遍历和后序遍历。这些遍历方式指的是节点访问的顺序。
前序遍历:在前序遍历中,我们首先访问根节点,然后递归地进行左子树的前序遍历,接着递归地进行右子树的前序遍历。
中序遍历:中序遍历中,我们首先递归地进行左子树的中序遍历,然后访问根节点,最后递归地进行右子树的中序遍历。
后序遍历:后序遍历中,我们首先递归地进行左子树的后序遍历,然后递归地进行右子树的后序遍历,最后访问根节点。
而这里呢我们又遇到了老朋友递归
问题不大
我们利用一棵树为例子

图中的这一棵树
以一为根
接下来我们先进行前序遍历
1.1.1前序遍历
前序遍历中先根后左右
●所以我们先去访问根1
●访问完根1后就访问左节点2
●接下来以2为根访问2的左节点3
●然后以3为根访问3的左节点,这是他的左节点为空,所以我们返回也就是开始进行递归
●递归到一后,开始进行访问1的右节点4
●访问到四就以4为根访问4的左节点5
●访问5后发现没有左节点就递归到4访问4的右节点
●访问6时没有左节点右节点就开始递归到4再到1
●最后访问结束
这里呢,我们用N代表空
那么访问完打印后应该是这样的
1 2 3 N N N 4 5 N N 6 N N
1.1.2中序遍历
讨论完前序遍历我们进行中序遍历
中序遍历讲的是先左后根最后右
还是利用这棵树

遍历顺序:
●先是访问左子树,1的左子树是2,2的则是3,3没有了左子树也就是空,返回3,然后在访问3的右子树,空,返回到2
这是返回的应该是
N 3 N●回到2后访问2的左子树空,所以返回到1
N 3 N 2 N●回到一就访问1的右子树4,然后到4的左子树5,在访问5的左子树空,这时返回到5
N 3 N 2 N 1 N 5 N这时会有疑问,为什么没有四,不是先访问到4吗?
这里没有4的原因是,返回到1后应该访问它的右子树,而右子树中还有一个左子树5,所以应该先访问5,这里的5优先访问
●然后返回到4,访问4的右子树6,这里优先访问6的左子树,为空,返回到6,访问右子树,为空
N 3 N 2 N 1 N 5 N 4 N 6 N
1.1.3后序遍历
后序遍历则是先左后右最后根
遍历顺序:
还是以这棵树为例
●先访问1的左子树,到3时,他的左子树为空,右子树为空
N N 3●返回到2后,右子树为空,访问根2,返回1
N N 3 N 2●回到一后,访问一的右子树,同时优先访问右子树中的左子树也就是节点五,访问五的左子树,然后是右子树,然后是五
N N 3 N 2 N N 5●J返回到五后访问4的右子树6,然后访问6的左子树和右子树
N N 3 N 2 N N 5 N N 6●访问完6后就返回访问4,然后访问1
N N 3 N 2 N N 5 N N 6 4 12.遍历代码的实现
2.1.树的实现
首先我们需要手搓一棵树
定义出来树的结构
并需要创建新的空间,所以这里包装一个函数
typedef struct BinTreeNode
{struct BinTreeNode* left;struct BinTreeNode* right;int val;
}BTNode;
BTNode* BuyBTNode(int val)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc fail");return NULL;}newnode->val = val;newnode->left = NULL;newnode->right = NULL;return newnode;
}
// 手搓一棵树
BTNode* CreateTree()
{BTNode* n1 = BuyBTNode(1);BTNode* n2 = BuyBTNode(2);BTNode* n3 = BuyBTNode(3);BTNode* n4 = BuyBTNode(4);BTNode* n5 = BuyBTNode(5);BTNode* n6 = BuyBTNode(6);n1->left = n2;n1->right = n4;n2->left = n3;n4->left = n5;n4->right = n6;return n1;
}这样就形成了图形中的树
2.2前序遍历代码
前序遍历的话我们需要用到递归
首如果检测到节点为空,这样的话就打印N并返回
如果没有
那么递归继续往下
因为是前序遍历
所以先递归左然后再递归右
void PreOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->val);PreOrder(root->left);PreOrder(root->right);
}2.3中序遍历代码
中序遍历和前序遍历的不同是前序遍历先根后左右,中序遍历则是先左后根最后右
所以,我们还是先遇到空返回N
没有则是返回左,打印根ra
void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}
2.4后序遍历代码
后序遍历代码则是先左右最后根
所以
void PostOrder(BTNode* root)
{if (root = NULL){printf("N");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}2.5测试的结果
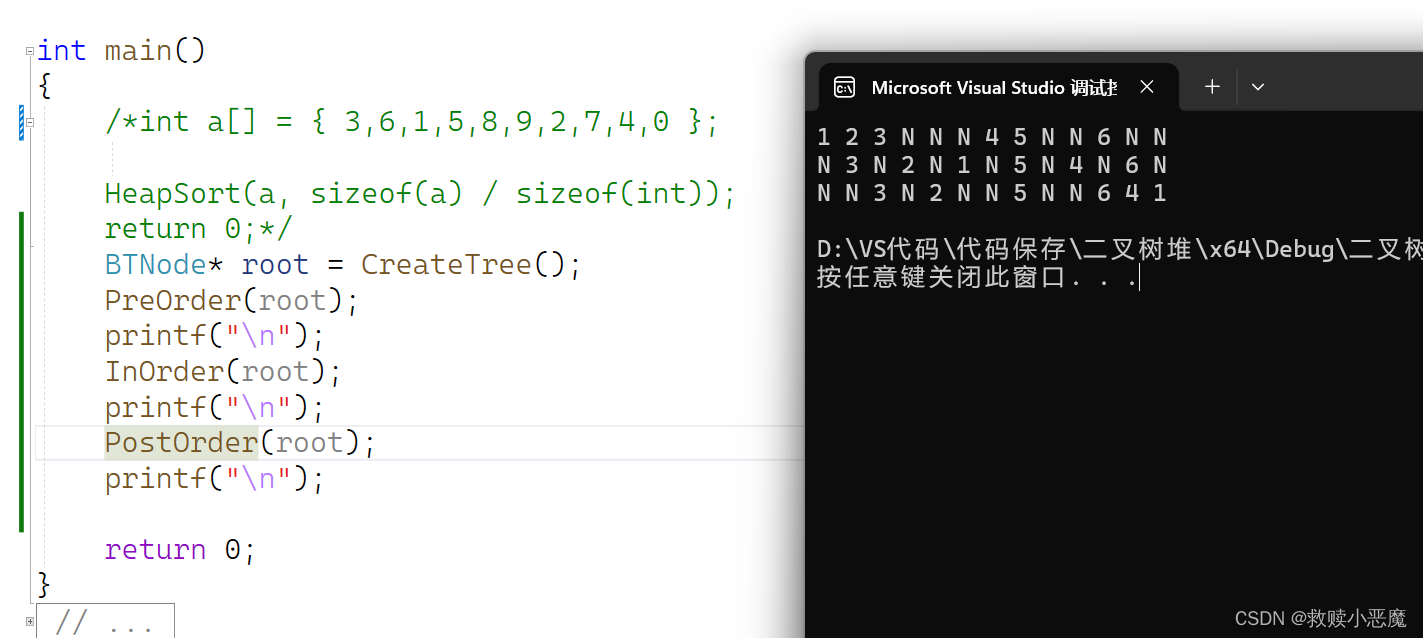
3.获取节点个数
获取节点个数,正常情况下我们的思路是定义一个size
然后在遍历的时候进行++size
代码如下
int TreeSize(BTNode* root)
{static int size = 0;if (root == NULL)return 0;else++size;TreeSize(root->left);TreeSize(root->right);return size;
}但这样会有一个缺点
我们没法去在这个函数里面重置我们的size
所以我们需要再主函数中
每调用完TreeSize函数,就需要重置一遍size
所以我们还有另外一个思路
直接去返回它的左节点和右节点,最后加一
利用递归的思想
代码如下
int TreeSize(BTNode* root)
{return root == NULL ? 0 :TreeSize(root->left) + TreeSize(root->right) + 1;
}这样就非常巧妙的完成了节点的个数
1.获取叶节点个数
获取叶子结点个数,我们这里也用递归的方法
利用分治思想去解决这个问题
●代码思想:
1. 当遇到空树或者遇到空的节点时,也就是说这是的叶子为NULL,这是我们返回0
2. 当遇到左节点或者右节点为空,当节点不为空时,此时已经到达了叶子结点,所以返回1
3. 当遇到的不是叶节点时,我们需要到递归左节点的个数和右节点的个数,并进行递归返回
●代码思想:
对于整棵树来说,当我们遇到空树或者遇到节点为空的时候,这时的叶子结点为空,我们这时返回0,当不是上中情况的时候,我们从根往下去搜索,先搜索左节点,当左节点不为空,并且左节点的左子树和右子树都是空的时候,这时候就可以确定它是叶子了,也就是返回1,当搜索完左子树就可以搜索右子树,右子树也同理 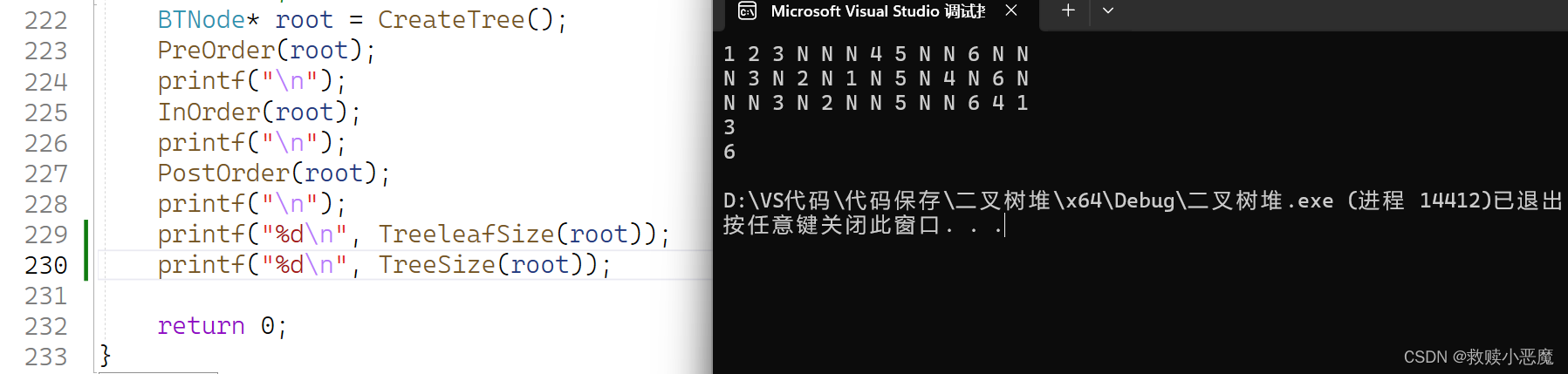
4.获取树的高度
获取树的高度,我们也是利用分治的思想去实现这个代码
首先就是当我们要想返回高度的时候,我们需要调用到左右子树的高度
然后比较左右子树的高度,比较出最大的一个并返回
然后加1(因为我们递归的是左右子树的高度,我们需要整个树的高度,所以还需要加上根,也就是加一)
●代码思想:
1.当我们遇到空树或者遇到的节点为NULL,这时返回0
2.然后接下来去递归左子树和右子树
3.返回时,如果左子树大于右子树,那么就是左子树高度+1,否则右子树高度+1
//获取树的高度
int TreeHeight(BTNode* root)
{if (root == NULL){return 0;}TreeHeight(root->left);TreeHeight(root->right);return (TreeHeight(root->left) > TreeHeight(root->right) ? TreeHeight(root->left) : TreeHeight(root->right)) + 1;
}
但这个代码有一定的缺陷
我们可以看到,这个代码我们调用了两次TreeHeight(root->left)和TreeHeight(root->right)
在这一树中,我们调用多次函数,大大增加了计算的难度,在一棵小树中可能不明显,可当树更大时,这时候弊端就先显示出来了
所以我们可以改进一下代码,定义两个变量去接受返回值
然后比较两个返回值
//改进代码
int TreeHeight(BTNode* root)
{if (root == NULL){return 0;}/*TreeHeight(root->left);TreeHeight(root->right);return (TreeHeight(root->left) > TreeHeight(root->right) ? TreeHeight(root->left) : TreeHeight(root->right)) + 1;*/int Heightleft = TreeHeight(root->left);int Heightright = TreeHeight(root->right);return (Heightleft > Heightright ? Heightleft : Heightright + 1);
}

5.计算第K层节点个数
计算k层节点的个数,我们可以看成计算左节点的(k-1)层和右节点(k-1)层的节点个数
因为我们不算顶部节点所以应该是k-1
●代码思想:
首先是如果是空树或者当遇到叶子结点外的空节点时,返回0
当遇到k为1的时候,这时只有一个根,也就返回1
其余情况均利用递归思想,去递归左右子树,注意此时的k应该变成k-1
//计算树k层的节点个数
int TreeKCount(BTNode* root, int k)
{if (root == NULL || k < 1){return 0;}if (k == 1){return 1;}return TreeKCount(root->left, k - 1) + TreeKCount(root->right, k - 1);
} 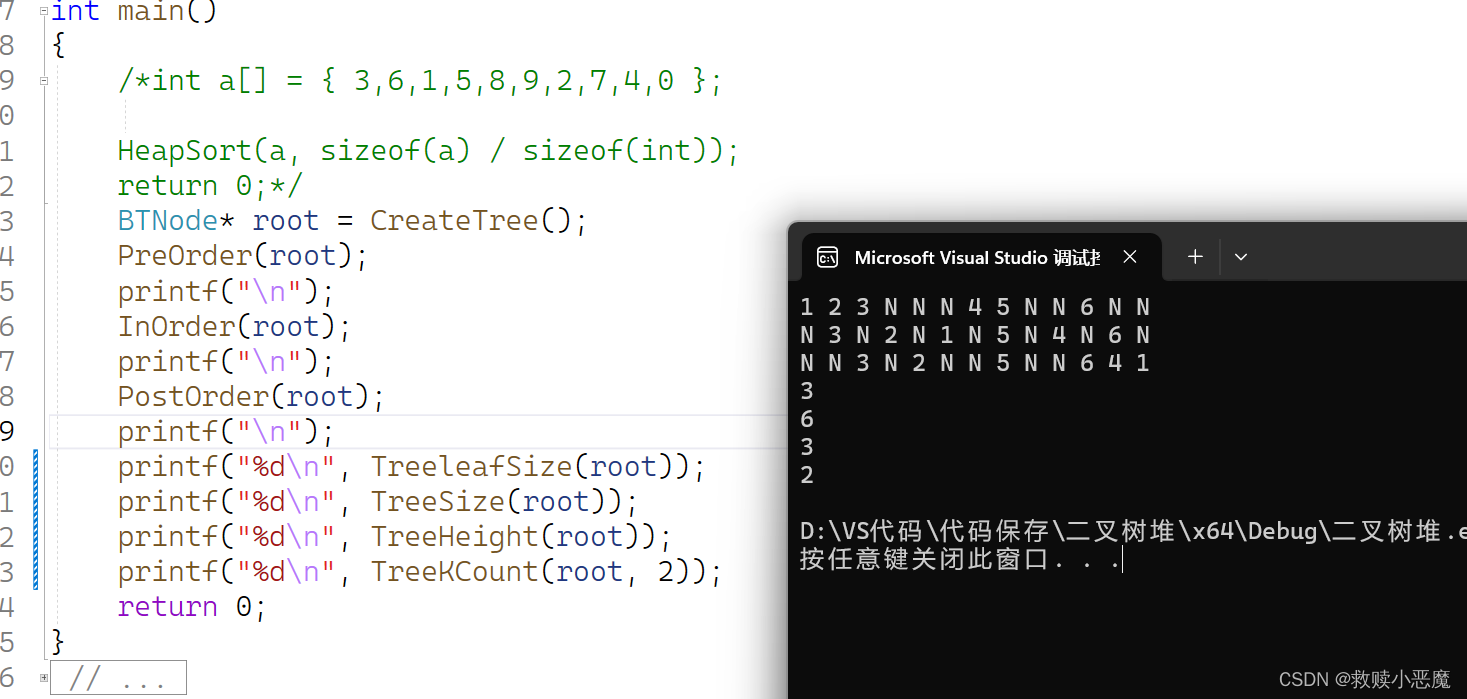
6.寻找某个节点
寻找某个节点的话,我们也利用递归的方法,分治的思想去解决这个问题
寻找某个节点,那么这个节点如果不在根上,那么就在根的左子树和右子树上
那么就想下寻找
下边的节点也可以分为左子树和右子树和根
依次进行,就形成了递归
//寻找某个节点
BTNode* TreeFind(BTNode* root, int x)
{if (root == NULL){return 0;}if (x == root->val){return root;}TreeFind(root->left, x);TreeFind(root->right, x);return NULL;
}很多人可能会想到这样的代码
可当我们去运行的时候,我们会发现找不到,不管x为多少都找不到
为什么呢?
原因是我们没有东西去接收
当我们找到的时候,我们递归需要往上递归
可上边的栈中没有可以接受的变量值
所以我们最终遍历完整棵树也找不到我们想找的节点
所以改一下代码
//寻找某个节点
BTNode* TreeFind(BTNode* root, int x)
{if (root == NULL){return 0;}if (x == root->val){return root;}BTNode* ret1 = TreeFind(root->left, x);BTNode* ret2 = TreeFind(root->right, x);if (ret1)return ret1;if (ret2)return ret2;return NULL;
}
这样我们利用新建立的节点去接受我们的左右子树的数据
然后如果不为空就不断返回,为空那么就返回0