穷举深搜暴搜回溯剪枝(2)-编程知识

一)电话号码的字母组合

17. 电话号码的字母组合 - 力扣（LeetCode）

1)画出决策树:只是需要对最终的决策树做一个深度优先遍历

把图画出来，知道每一层在干什么，代码就能写出来了

2)定义全局变量:

1)定义一个哈希表来处理数字和字符串的映射关系

2)使用ret来保存最终结果

class Solution {HashMap<Character,String> result=new HashMap<>();List<String> ret;StringBuilder path;public List<String> letterCombinations(String digits) {this.path=new StringBuilder();result.put('2',"abc");result.put('3', "def");result.put('4', "ghi");result.put('5', "jkl");result.put('6', "mno");result.put('7', "pqrs");result.put('8', "tuv");result.put('9', "wxyz");this.ret=new ArrayList<>();if(digits.length()==0){return ret;}dfs(result,digits,0);return ret;}
public void dfs(HashMap<Character,String> result,String digits,int index){if(index==digits.length()){
//这个最终条件,第一次就写错了,index遍历到数组的最后一个位置ret.add(path.toString());return;}Character number=digits.charAt(index);String string=result.get(number);char[] chars=string.toCharArray();for(int i=0;i<chars.length;i++){path.append(chars[i]);
//继续遍历到下一层dfs(result,digits,index+1);
//恢复现场,回退到上一层path.deleteCharAt(path.length()-1);}}
}

二)括号生成:

22. 括号生成 - 力扣（LeetCode）

先进行想一下，什么是有效的括号组合？

1)左括号的数量==有括号的数量

2)从头开始的任意一个子串中，左括号的数量都是大于等于右括号的数量，如果发现右括号的数量是大于左括号的，那么必然会出现一个右括号没有做括号匹配，所以就不是一个有效的括号组合

假设如果n==3，那么我们只是需要枚举6个位置即可，因为n==3表示的是三对括号，一共有6个位置，那么我们只是需要进行暴力枚举6个位置可能出现的情况就可以了

一)画出决策树:

二)定义一个全局变量:

1)left表示左括号的数量，right表示右括号的数量，N表示一共有多少对括号

2)当进行深度优先遍历的时候，使用这个path变量来进行记录这个路径中曾经出现过的括号

三)dfs所干的事:

当左括号合法的时候，把左括号添加到path中当右括号合法的时候，把右括号添加到path中

四)递归:遇到叶子节点的时候，将这个path添加到ret中，遇到叶子节点的情况就是当right==N的时候，说明此时右括号已经满了
class Solution {int N;StringBuilder path;List<String> ret;int right=0;int left=0;public List<String> generateParenthesis(int n) {N=n;path=new StringBuilder();ret=new ArrayList<>();dfs();return ret;}public void dfs(){if(right==N){ret.add(path.toString());return;}//选择左括号if(left<N){path.append('(');left++;dfs();//回溯恢复现场left--;path.deleteCharAt(path.length()-1);}if(right<left){path.append(')');right++;dfs();//回溯恢复现场right--;path.deleteCharAt(path.length()-1);}}
}
其实本质上来说把刚才的那些全局变量放到参数里面，只是回溯时候的操作是不一样的

三)组合:

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

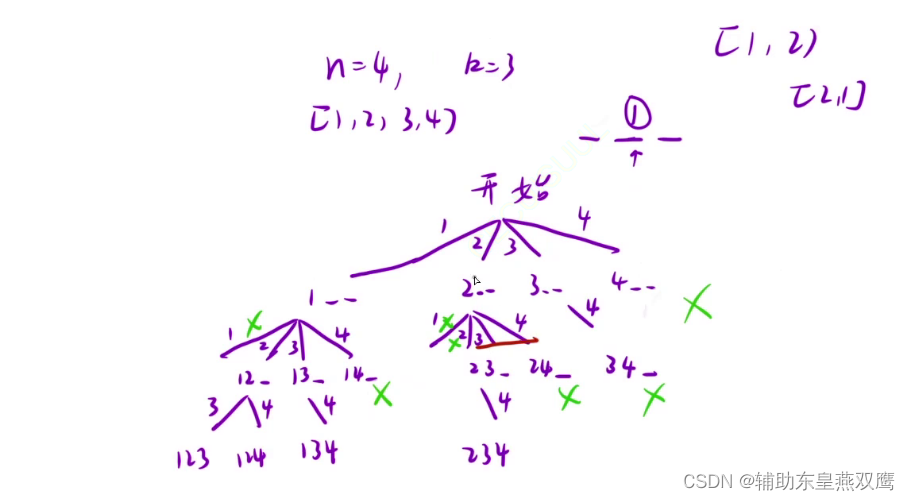
1)实现剪枝的操作:当我们进行枚举当前数的时候，只需要从当前数的下一个数字开始进行枚举就可以了，只需要控制dfs的参数即可

2)dfs做的事:从pos位置开始进行枚举，将枚举的情况添加到path中即可

3)回溯:当枚举完成当前位置向上归的过程中，先把path中添加的数进行剔除，然后再返回到上一层即可

4)递归出口:k==path.size()
class Solution {List<List<Integer>> ret;List<Integer> path;int N;int k;public List<List<Integer>> combine(int n, int k) {N=n;this.k=k;path=new ArrayList<>();ret=new ArrayList<>();dfs(1);return ret;}public void dfs(int index){if(path.size()==k) {ret.add(new ArrayList<>(path));return;}for(int i=index;i<=N;i++){path.add(i);dfs(i+1);path.remove(path.size()-1);}}
}

四)目标和

494. 目标和 - 力扣（LeetCode）

中心思想:

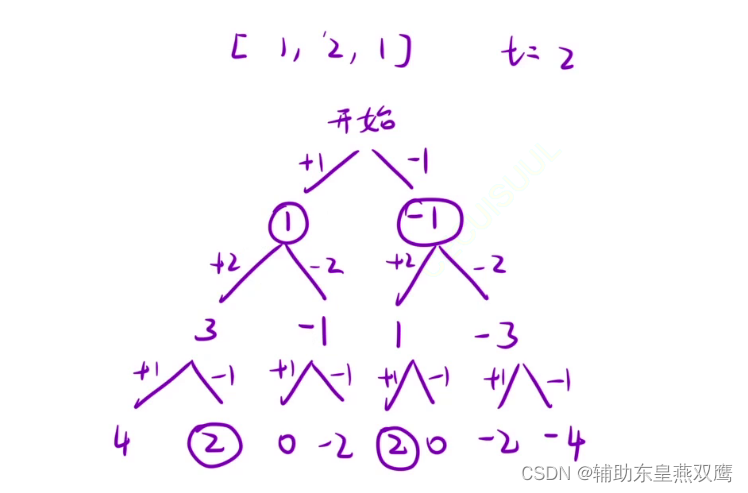
1)就是在第一个数前面+1或者是进行-1操作，变量作为全局变量还是函数中的参数来说，作为全局变量是需要考虑一下回溯，作为参数的话是不需要进行考虑回溯操作的，因为代码本身已经帮助我们递归向下进行向上返回的过程中已经帮助我们完成回溯操作了

2)当作为参数的时候，递归函数本身归的过程中已经在帮助我们进行回溯操作了，当int作为参数，数组类型作为全局的时候写法是比较方便的
class Solution {int count=0;int target=0;int path=0;public int findTargetSumWays(int[] nums, int target) {this.target=target;dfs(nums,0);return count;}public void dfs(int[] nums,int pos){if(pos==nums.length){if(path==target) count++;return;}
//当前这个数取正数的情况path+=nums[pos];//pos的作用是记录数组下标dfs(nums,pos+1);//回溯path-=nums[pos];
//当前这个数取负数的情况path-=nums[pos];dfs(nums,pos+1);//回溯path+=nums[pos];}
}
class Solution {int count=0;int target=0;public int findTargetSumWays(int[] nums, int target) {this.target=target;dfs(nums,0,0);return count;}public void dfs(int[] nums,int path,int pos){if(pos==nums.length){if(path==target){count++;}return;}dfs(nums,path+nums[pos],pos+1);//回来的就是原来的现场dfs(nums,path-nums[pos],pos+1);}
}

五)组合总和(1):

39. 组合总和 - 力扣（LeetCode）

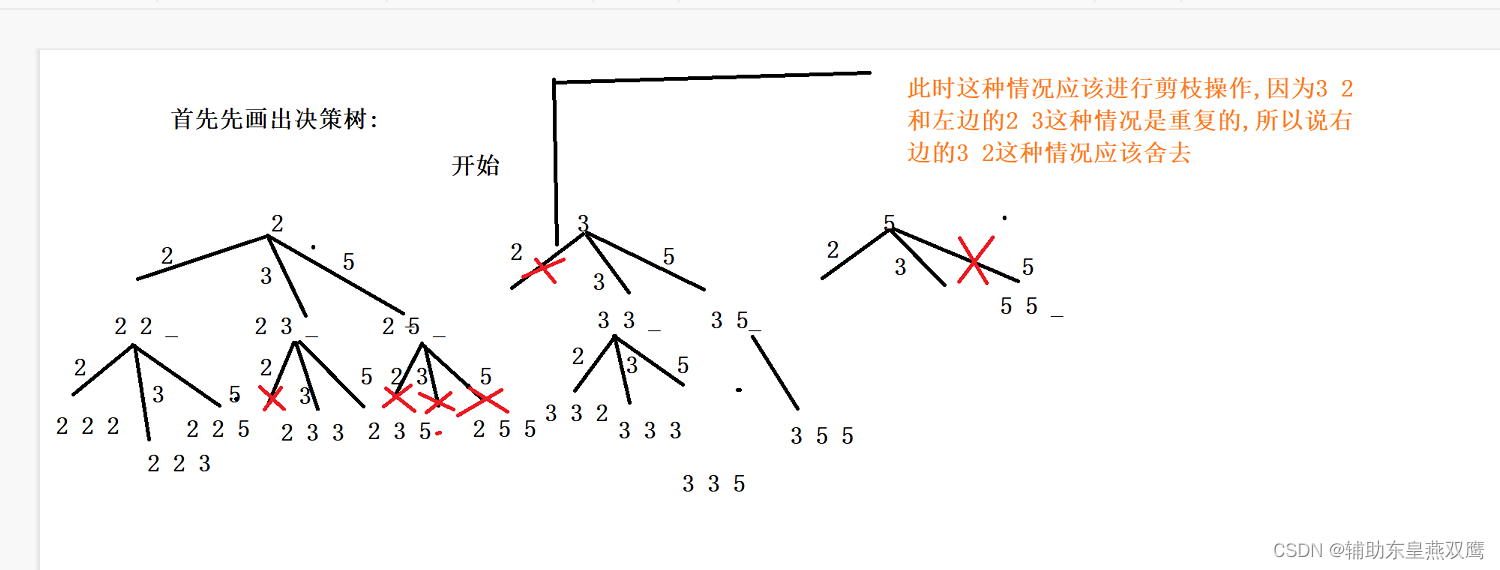
1)没有一成不变的模板，只需要将决策树画出来，将最终的决策树转化成代码即可

2)反正这个题就是你从目标的元素里面找到几个数这几个数进行相加的结果等于target即可

3)所以这个题的中心思想就是一个数一个数，两个数，两个数的进行考虑

4)第一个位置可以存放2，可以存放3，可以存放5

解法1:

class Solution {List<List<Integer>> ret;int sum=0;List<Integer> path;int target=0;public List<List<Integer>> combinationSum(int[] nums, int target) {ret=new ArrayList<>();path=new ArrayList<>();this.target=target;Arrays.sort(nums);dfs(nums,0);return ret;}public void dfs(int[] nums,int index){if(sum==target){ret.add(new ArrayList<>(path));return;}
//index这个参数表示的是这一层循环从数组中的哪一个位置开始进行枚举for(int i=index;i<nums.length;i++){path.add(nums[i]);sum+=nums[i];if(sum>target){sum-=nums[i];path.remove(path.size()-1);
//如果说当前的数加起来的和已经都大于target了,那么后续都无需进行遍历了,因为此时数组是有序的,直接回退到上一层即可return;} dfs(nums,i);//下一次遍历的位置还是可以从当前位置开始进行遍历,这里面是可以选择重复元素sum-=nums[i];path.remove(path.size()-1);}}
}

class Solution {List<List<Integer>> ret;int sum=0;List<Integer> path;int target=0;public List<List<Integer>> combinationSum(int[] nums, int target) {ret=new ArrayList<>();path=new ArrayList<>();this.target=target;Arrays.sort(nums);dfs(nums,0);return ret;}public void dfs(int[] nums,int index){if(sum>target) return;if(sum==target){ret.add(new ArrayList<>(path));return;}for(int i=index;i<nums.length;i++){path.add(nums[i]);sum+=nums[i];dfs(nums,i);
//枚举到下一层的时候回溯到当前结点的时候进行恢复现场的操作sum-=nums[i];path.remove(path.size()-1);}}
}

下面是当sum是局部变量的时候，所进行传递的值:

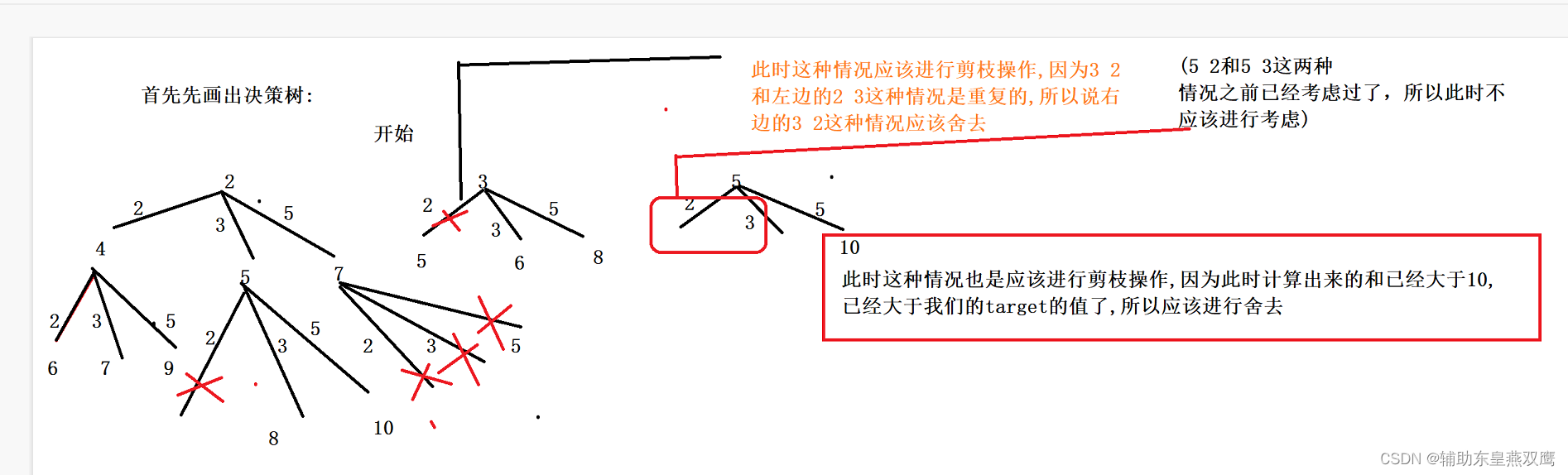
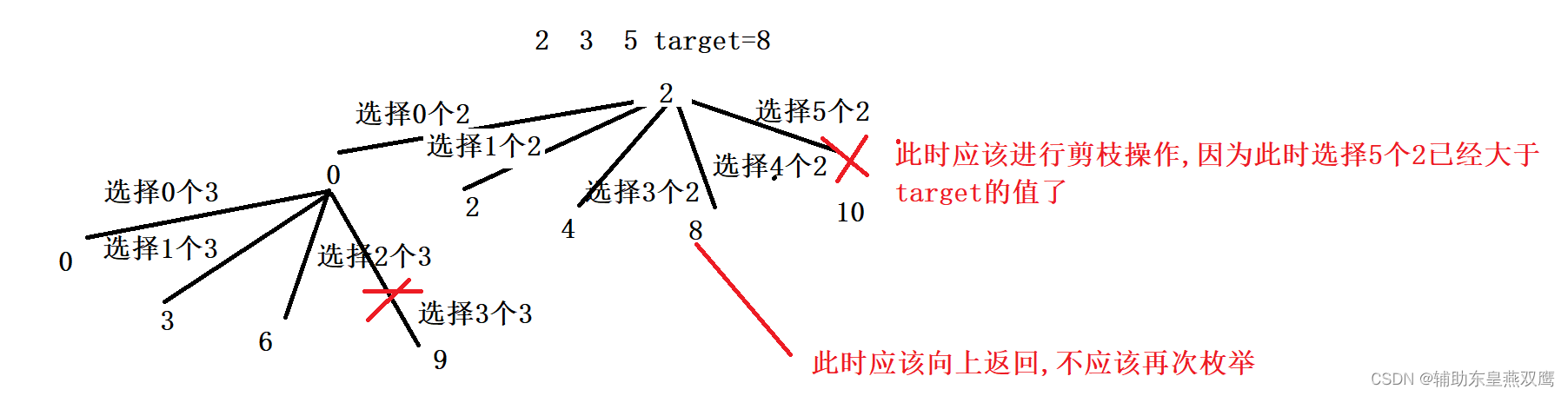
解法2:根据选取数的个数来画出决策树:

每一个数我可以选择0个，1个，可以选择2个，可以选择3个，可以选择4个

我们告诉dfs一个位置，枚举1个，两个，三个，只要小于8即可，只要枚举的个数*这个数<8即可，添加到path路径中，接下来去下一层开始走

当我们枚举完9的时候才会向上恢复现场的，因为假设如果枚举到3的时候才向上恢复现场，那么6的情况必定会被丢弃掉，因为后面的数是在前面的数的基础上+3的，后面的数要依赖于前面的数，所以当我们将这一层的所有的数处理完成之后才会恢复现场
class Solution {List<List<Integer>> ret;List<Integer> path;int target=0;int sum=0;public List<List<Integer>> combinationSum(int[] nums, int target) {ret=new ArrayList<>();path=new ArrayList<>();this.target=target;dfs(nums,0);return ret;}public void dfs(int[] nums,int index){if(sum>target){return;} if(sum==target){ret.add(new ArrayList<>(path));return;}if(index==nums.length) return;int pos=0;for(int i=0;sum<target;i++){if(i!=0){path.add(nums[index]);sum+=nums[index];pos++;}dfs(nums,index+1);}while(pos>0){sum-=nums[index];path.remove(path.size()-1);pos--;//记录加了多少次}}
}

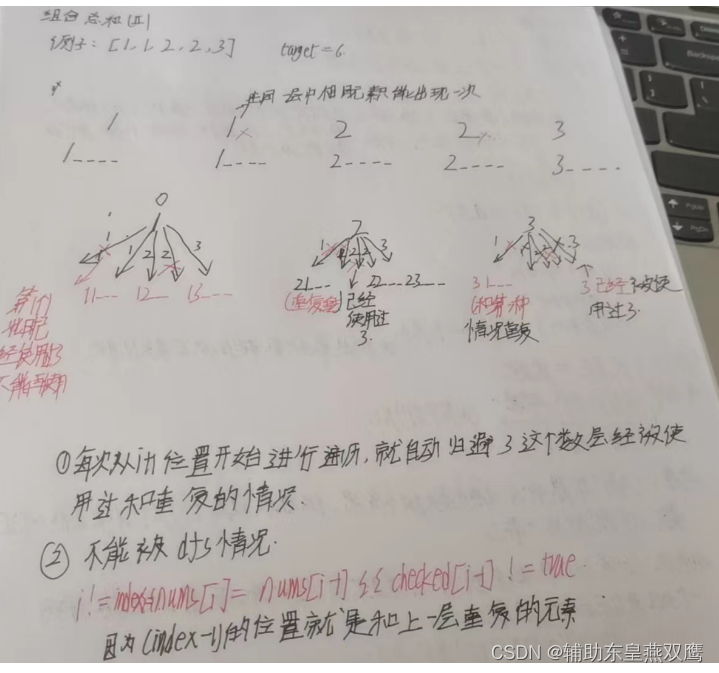
六)组合总和(2)

39. 组合总和 - 力扣（LeetCode）

class Solution {int sum=0;int target=0;List<List<Integer>> ret;List<Integer> path;boolean[] used;public List<List<Integer>> combinationSum2(int[] nums, int target) {this.ret=new ArrayList<>();this.path=new ArrayList<>();this.target=target;this.used=new boolean[nums.length];Arrays.sort(nums);dfs(nums,0);return ret;}public void dfs(int[] nums,int index){if(sum>target) return;if(sum==target){ret.add(new ArrayList<>(path));return;}for(int i=index;i<nums.length;i++){if(i!=index&&used[i-1]!=true&&nums[i]==nums[i-1]){continue;}path.add(nums[i]);sum+=nums[i];used[i]=true;dfs(nums,i+1);used[i]=false;sum-=nums[i]; path.remove(path.size()-1);}}
}

七)路经总和

112. 路径总和 - 力扣（LeetCode）

解法1:找到二叉树的所有路径和，把他存放到一个list里面

相同子问题:跟定一个根节点，求以根节点为树的所有路径和

递归出口:当进行遍历到叶子结点的时候

dfs:向下一直找到叶子节点，如果遇到叶子节点，就把sum+root.val存放到最终结果中
class Solution {public int sum=0;List<Integer> list=new ArrayList<>();public boolean hasPathSum(TreeNode root, int targetSum) {if(root==null) return false;dfs(root,0);return list.contains(targetSum);}public void dfs(TreeNode root,int sum){if(root.left==null&&root.right==null){
//与到叶子节点的时候才会进行计数,找到递归的出口list.add(sum+root.val);return;}if(root.left!=null) dfs(root.left,sum+root.val);if(root.right!=null) dfs(root.right,sum+root.val);}
}
解法2:使用回溯的方式，也是找到重复子问题:

1)观察我们要找的所有函数，我们可以查询出它的功能:询问是否从当前节点root到达叶子节点的路径，找到满足于路径和等于sum，假设从根节点到达当前节点的和是temp，那么我们只是需要找到是否从当前节点到达叶子节点，找到和等于sum-temp的叶子的路径，满足路径之和等于sum-temp

2)递归出口:当遍历到叶子结点的时候，判断sum-temp==true
class Solution {public boolean hasPathSum(TreeNode root, int targetSum) {if(root==null) return false;if(root.left==null&&root.right==null){return root.val==targetSum;}
return hasPathSum(root.left,targetSum-root.val)||hasPathSum(root.right,targetSum-root.val);}
}

八)路经总和(2)

class Solution {List<Integer> path;List<List<Integer>> ret;int targetSum;int sum;public List<List<Integer>> pathSum(TreeNode root, int targetSum) {this.path=new ArrayList<>();this.ret=new ArrayList<>();this.targetSum=targetSum;dfs(root);return ret;}public void dfs(TreeNode root){if(root==null) return;if(root.left==null&&root.right==null){path.add(root.val);sum+=root.val;if(sum==targetSum){ret.add(new ArrayList<>(path));}sum-=root.val;path.remove(path.size()-1);
//此时遍历到叶子结点的时候还是需要向上进行回溯操作return;}path.add(root.val);sum+=root.val;dfs(root.left);
//向上回溯,恢复现场sum-=root.val;path.remove(path.size()-1);path.add(root.val);sum+=root.val;dfs(root.right);
//向上回溯,恢复现场sum-=root.val;path.remove(path.size()-1);}
}

九)组合总和(3)

216. 组合总和 III - 力扣（LeetCode）

class Solution {List<Integer> path;List<List<Integer>> ret;int sum=0;int n=0;int target;public List<List<Integer>> combinationSum3(int n, int target) {this.path=new ArrayList<>();this.target=target;this.n=n;this.ret=new ArrayList<>();dfs(1);return ret;}public void dfs(int index){if(path.size()>n) return;if(sum==target&&path.size()==n){ret.add(new ArrayList<>(path));return;}for(int i=index;i<=9;i++){path.add(i);sum+=i;dfs(i+1);sum-=i;path.remove(path.size()-1);}}
}