在上一篇博客中讲解了堆，现在来讲讲基于堆实现的排序，即堆排序。

要用堆排序，首先我们需要先建堆，建堆有两种方法：向上调整法建堆和向下调整法建堆。接下来我们分析这两种方法的时间复杂度。

向上调整法：

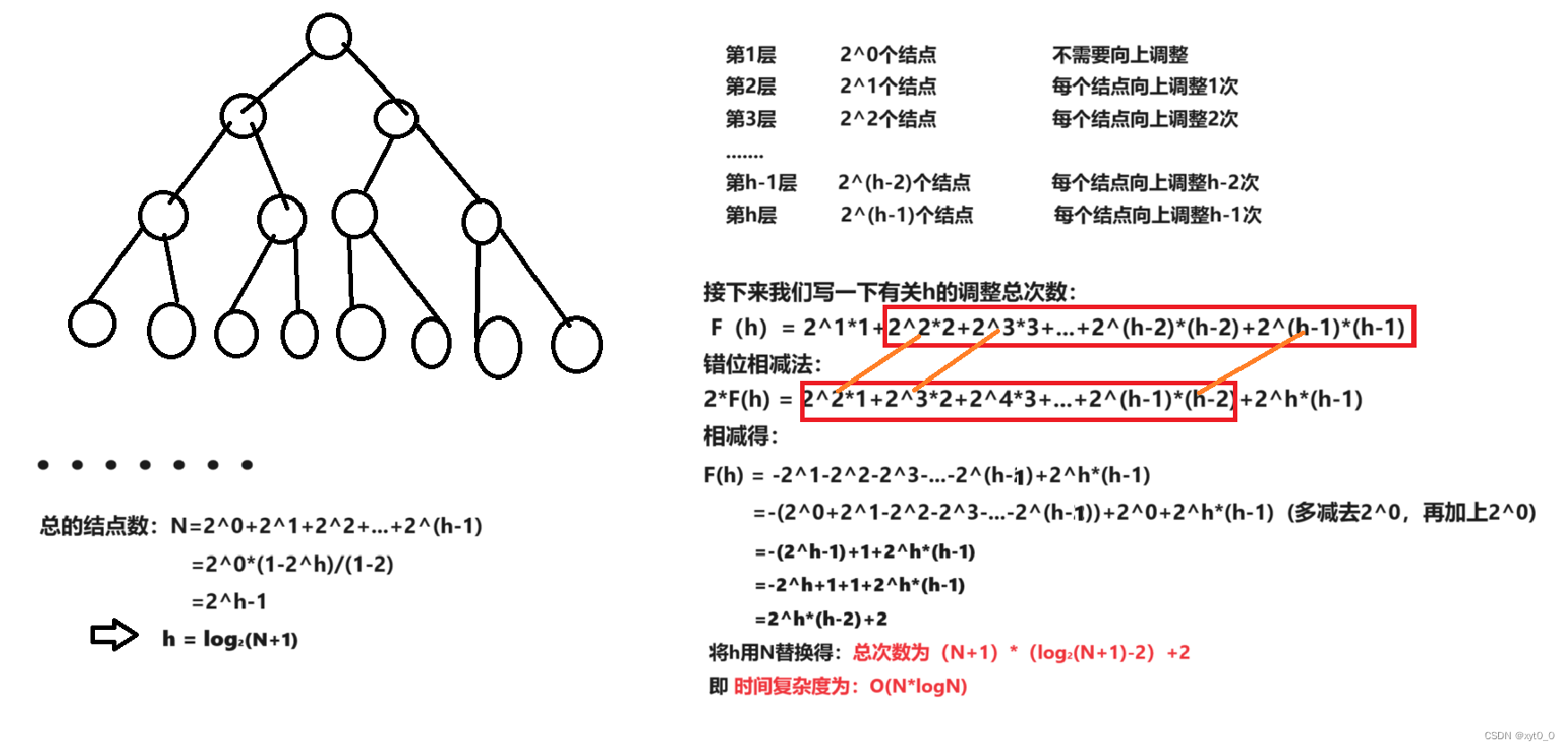
向下调整法： 

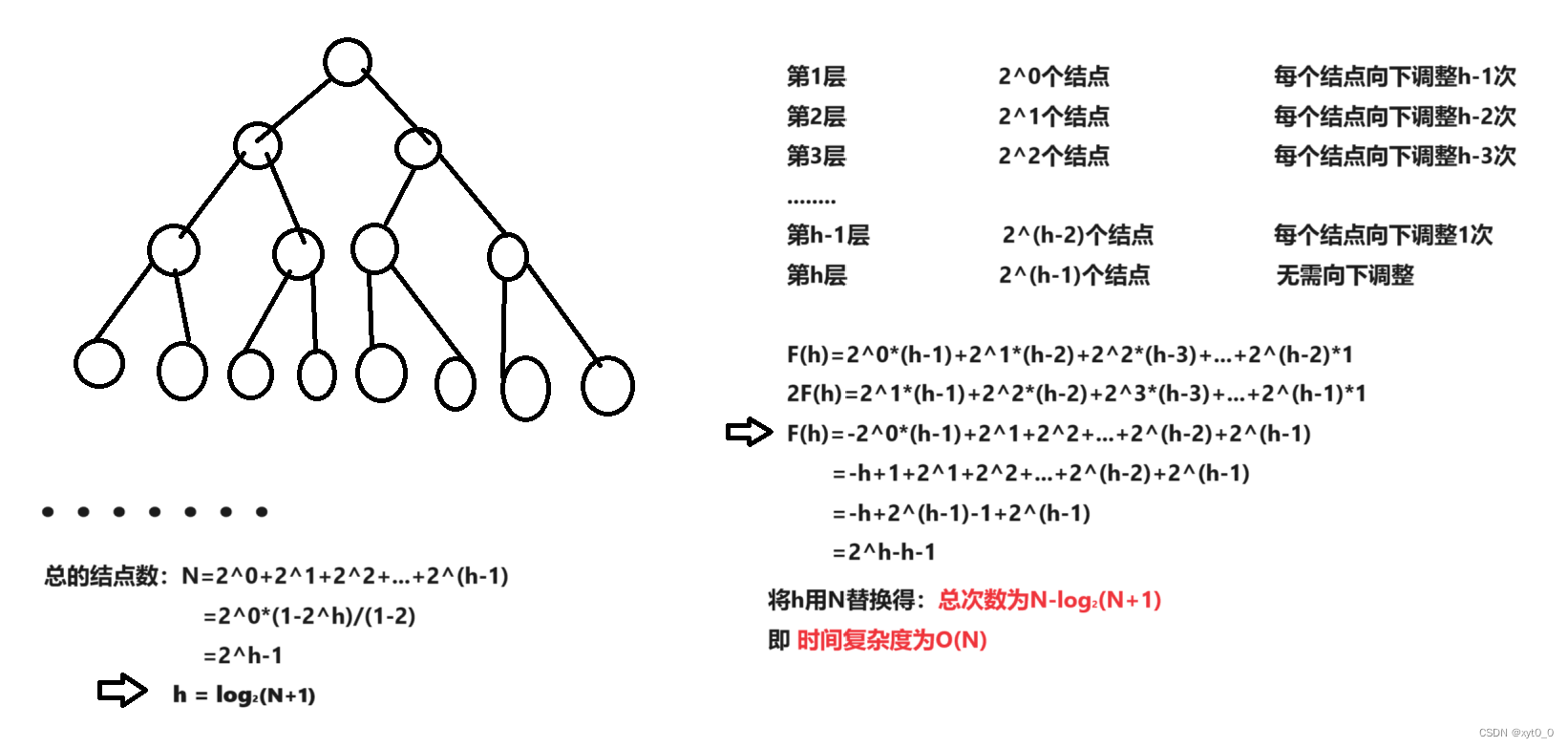
根据上面的分析，我们得到：向下调整法建堆更高效，所以接下来的堆排序实现过程中我们用向下调整法建堆。向下调整法建堆需要从第一个非叶子结点开始，然后调整完后调整上边的（即从下往上），如果从下标为0的结点开始向下调整会有问题，因为我们调整时是交换孩子和父亲，而当其深度大于2时，并且在后边（隔了几层）有更小的数时，交换后是无法保证最小的数在堆顶的，因为这时候是按照从上往下的顺序进行向下调整，在下边的更小的数是不能再往上交换的（除了其父父亲）。

接下来我们分析实现堆排序的过程。

排序有升序和降序，而堆中有大堆和小堆，我们应该建大堆还是小堆呢？答案是升序建大堆，降序建小堆。

我们知道，大堆中堆顶元素是所有元素中最大的那个，小堆中堆顶元素是所有元素中最小的那个，堆排序便是依次来实现的。以降序为例，给定一个有n个元素的数组，当我们建好堆后，我们不断把堆顶元素与最后一个元素交换，这样最后一个元素就放好了，然后重新调整为小堆，在下一次交换时，针对的就是前n-1个数据了，然后一直这样交换下去，这便是堆排序的思想。

接下来上代码： 

//交换数据
void swap(HPDataType* x, HPDataType* y)
{HPDataType t = 0;t = *x;*x = *y;*y = t;
}//向下调整
void AdjustDown(HPDataType* a, int size, int parents)
{int child = parents * 2 + 1;//左孩子while (child < size){//如果右孩子更小，交换//注意child+1<size这个条件，实际最多只能访问到size-1的数据if (child + 1 < size && a[child] > a[child + 1]){child++;}if (a[child] < a[parents]){swap(&a[child], &a[parents]);parents = child;child = parents * 2 + 1;}else{break;}}
}//堆排序
void HeapSort(HPDataType* a, int n)
{//数组建堆（向下调整）int i = 0;//(n-1-1)/2是第一个非叶子结点for (i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}//最后一个数下标int end = n - 1;while (end > 0){swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;//注意调整和自减顺序，end是最后一个数的下标，交换完后，前边的数的个数即end}
}int main()
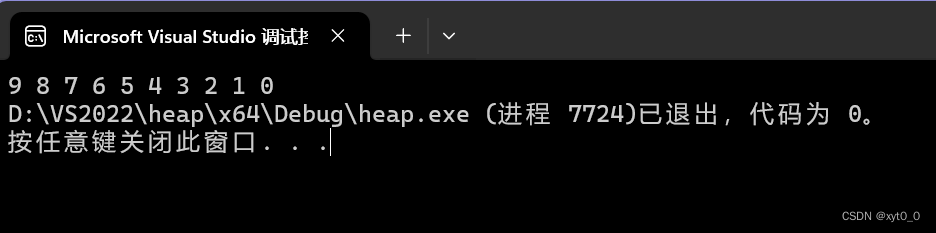
{int arr[10] = { 1,8,6,4,2,7,3,5,9,0 };HeapSort(arr, 10);int i = 0;for (i = 0; i < 10; i++){printf("%d ", arr[i]);}return 0;
}

 测试结果：