单调队列优化DP

最大子序和 

输入一个长度为 n 的整数序列，从中找出一段长度不超过 m的连续子序列，使得子序列中所有数的和最大。

注意： 子序列的长度至少是 1。

输入格式

第一行输入两个整数 n,m。

第二行输入 n 个数，代表长度为 n 的整数序列。

同一行数之间用空格隔开。

输出格式

输出一个整数，代表该序列的最大子序和。

数据范围

1≤n,m≤300000
保证所有输入和最终结果都在 int 范围内。

输入样例：

6 4
1 -3 5 1 -2 3

输出样例：

7

时间复杂度：O（n） 

看到求一段区间的最大值 --联想到用前缀和去解决 --去思考怎么样去枚举区间

暴力枚举 O(nm)

不妨以i为右端点 f[i]max=(s[i]-(s[j])min) j是在 i与m 允许的区间中

 s[j]最m区间最小--单调队列 --单调递增队列

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=3e5+10;
ll s[N];
ll q[N];
int n,m;
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%lld",&s[i]);s[i]+=s[i-1];}int hh=0,tt=0;q[0]=0;ll res=-1e18;for(int i=1;i<=n;i++){//为什么不是 i-m+1 是因为求得是 前缀和相减 //比如 i=9 m=4 那存在的j最多是6 可是要求6-9之间的和 是s[9]-s[6-1]//所以这里应该往前多存一个while(hh<=tt&&q[hh]<i-m) hh++;res=max(res,s[i]-s[q[hh]]);while(hh<=tt&&s[i]<=s[q[tt]]) tt--;q[++tt]=i;}cout<<res<<endl;return 0;
}
#include<iostream>
#include<algorithm>
#include<deque>
using namespace std;
typedef long long ll;
const int N=3e5+10;
deque<ll>q;
ll s[N];
int main()
{int n,m;scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%lld",&s[i]);s[i]+=s[i-1];}q.push_back(0);ll res=-1e18;for(int i=1;i<=n;i++){while(q.size()&&q.front()<i-m) q.pop_front();res=max(res,s[i]-s[q.front()]);while(q.size()&&s[i]<=s[q.back()]) q.pop_back();q.push_back(i);}printf("%lld",res);return 0;
}

修剪草坪

在一年前赢得了小镇的最佳草坪比赛后，FJ 变得很懒，再也没有修剪过草坪。

现在，新一轮的最佳草坪比赛又开始了，FJ 希望能够再次夺冠。

然而，FJ 的草坪非常脏乱，因此，FJ 只能够让他的奶牛来完成这项工作。

FJ 有 N 只排成一排的奶牛，编号为 1 到 N。

每只奶牛的效率是不同的，奶牛 i 的效率为 Ei。

编号相邻的奶牛们很熟悉，如果 FJ 安排超过 K 只编号连续的奶牛，那么这些奶牛就会罢工去开派对。

因此，现在 FJ 需要你的帮助，找到最合理的安排方案并计算 FJ 可以得到的最大效率。

注意，方案需满足不能包含超过 K 只编号连续的奶牛。

输入格式

第一行：空格隔开的两个整数 N 和 K；

第二到 N+1 行：第 i+1 行有一个整数 Ei。

输出格式

共一行，包含一个数值，表示 FJ 可以得到的最大的效率值。

数据范围

1≤N≤10^5
0≤Ei≤10^9

输入样例：

5 2
1
2
3
4
5

输出样例：

12

样例解释

FJ 有 5 只奶牛，效率分别为 1、2、3、4、5。

FJ 希望选取的奶牛效率总和最大，但是他不能选取超过 2 只连续的奶牛。

因此可以选择第三只以外的其他奶牛，总的效率为 1 + 2 + 4 + 5 = 12。

奶牛换一个思路，考虑空位置，使空的位置的效率最低（从而总效率最大）。那就和烽火是一道题惹。 

#include<iostream>
#include<algorithm>
#include<cstring>
#include<deque>
using namespace std;
typedef long long ll;
const int N=2e5+10;
deque<ll>q;
ll a[N];
ll f[N];
int n,m;
ll sum=0;
int main()
{cin>>n>>m;for(int i=1;i<=n;i++) {cin>>a[i];sum+=a[i];}q.push_back(0);for(int i=1;i<=n;i++){while(q.size()&&q.front()<i-m-1) q.pop_front();f[i]=f[q.front()]+a[i];while(q.size()&&f[q.back()]>=f[i]) q.pop_back();q.push_back(i);}ll res=1e18;for(int i=n-m;i<=n;i++){res=min(res,f[i]);}cout<<sum-res<<endl;return 0;
}

 烽火传递

烽火台是重要的军事防御设施，一般建在交通要道或险要处。

一旦有军情发生，则白天用浓烟，晚上有火光传递军情。

在某两个城市之间有 n 座烽火台，每个烽火台发出信号都有一定的代价。

为了使情报准确传递，在连续 m 个烽火台中至少要有一个发出信号。

现在输入 n,m 和每个烽火台的代价，请计算在两城市之间准确传递情报所需花费的总代价最少为多少。

输入格式

第一行是两个整数 n,m，具体含义见题目描述；

第二行 n 个整数表示每个烽火台的代价 ai。

输出格式

输出仅一个整数，表示最小代价。

数据范围

1≤m≤n≤2×10^5
0≤ai≤1000

输入样例：

5 3
1 2 5 6 2

输出样例：

4

 

#include<iostream>
#include<algorithm>
#include<cstring>
#include<deque>
using namespace std;
const int N=2e5+10;
deque<int>q;
int a[N];
int f[N];
int n,m;
int main()
{cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i];q.push_back(0);for(int i=1;i<=n;i++){while(q.size()&&q.front()<i-m) q.pop_front();f[i]=f[q.front()]+a[i];while(q.size()&&f[q.back()]>=f[i]) q.pop_back();q.push_back(i);}int res=0x3f3f3f3f;for(int i=n-m+1;i<=n;i++){res=min(res,f[i]);}cout<<res<<endl;return 0;
}

绿色通道

二分答案+dp队列优化

 高二数学《绿色通道》总共有 n 道题目要抄，编号 1,2,…,n，抄第 i 题要花 ai 分钟。

小 Y 决定只用不超过 t 分钟抄这个，因此必然有空着的题。

每道题要么不写，要么抄完，不能写一半。

下标连续的一些空题称为一个空题段，它的长度就是所包含的题目数。

这样应付自然会引起马老师的愤怒，最长的空题段越长，马老师越生气。

现在，小 Y 想知道他在这 t 分钟内写哪些题，才能够尽量减轻马老师的怒火。

由于小 Y 很聪明，你只要告诉他最长的空题段至少有多长就可以了，不需输出方案。

输入格式

第一行为两个整数 n,t。

第二行为 n 个整数，依次为 a1,a2,…,an

输出格式

输出一个整数，表示最长的空题段至少有多长。

数据范围

0<n≤5×10^4
0<ai≤3000,
0<t≤10^8

输入样例：

17 11
6 4 5 2 5 3 4 5 2 3 4 5 2 3 6 3 5

输出样例：

3

 

#include<iostream>
#include<algorithm>
#include<deque>
#include<cstring>
using namespace std;
const int N=5e4+10;
int f[N],a[N];
int n,t;
bool check(int x)
{deque<int>q;q.push_back(0);memset(f,0,sizeof f);for(int i=1;i<=n;i++){while(q.size()&&q.front()<i-x-1) q.pop_front();f[i]=f[q.front()]+a[i];while(q.size()&&f[i]<=f[q.back()]) q.pop_back();q.push_back(i);}for(int i=n-x;i<=n;i++){if(f[i]<=t) return true;}return false;
}
int main()
{cin>>n>>t;for(int i=1;i<=n;i++) cin>>a[i];int l=0,r=n;while(l<r){int mid=(l+r)>>1;if(check(mid)) r=mid;else l=mid+1;}cout<<l<<endl;return 0;
}

理想的正方形(二维）

有一个 a×b 的整数组成的矩阵，现请你从中找出一个 n×n 的正方形区域，使得该区域所有数中的最大值和最小值的差最小。

输入格式

第一行为三个整数，分别表示 a,b,n 的值；

第二行至第 a+1 行每行为 b 个非负整数，表示矩阵中相应位置上的数。

输出格式

输出仅一个整数，为 a×b 矩阵中所有“n×n正方形区域中的最大整数和最小整数的差值”的最小值。

数据范围

2≤a,b≤1000
n≤a,n≤b,n≤100
矩阵中的所有数都不超过 10^9。

输入样例：

5 4 2
1 2 5 6
0 17 16 0
16 17 2 1
2 10 2 1
1 2 2 2

输出样例：

1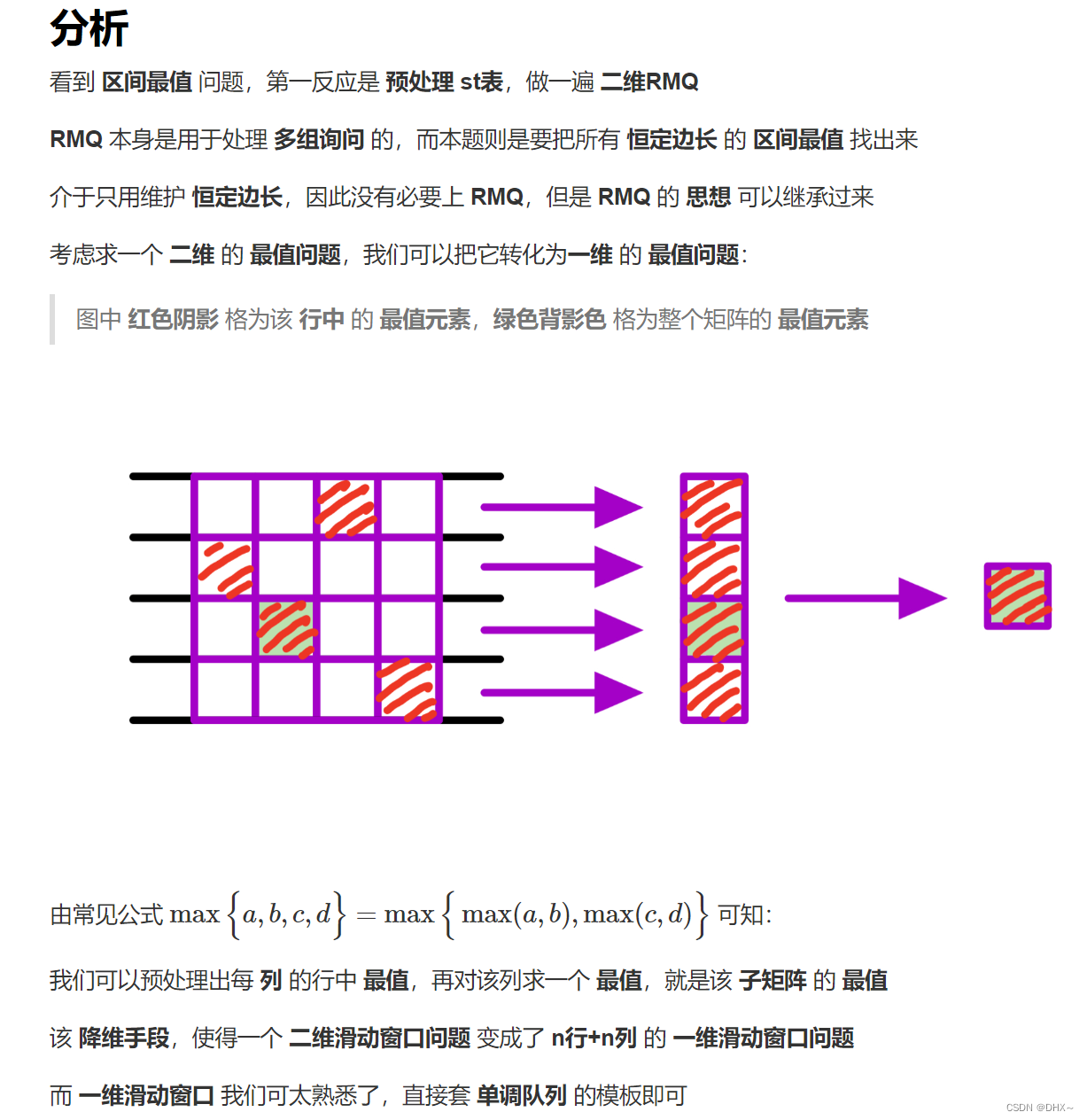

 这样写卡数据

#include<iostream>
#include<algorithm>
#include<deque>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=1e3+10;
ll max1[N][N],min1[N][N];
ll w[N][N],c[N][N];
int n,m,a,b;
int main()
{cin>>n>>m>>a;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++) cin>>w[i][j];for(int i=1;i<=n;i++){deque<ll>q;q.push_back(1);for(int j=1;j<=m;j++){while(q.size()&&q.front()<=j-a) q.pop_front();while(q.size()&&w[i][j]>=w[i][q.back()]) q.pop_back();q.push_back(j);max1[i][j]=w[i][q.front()];}}for(int i=1;i<=n;i++){deque<ll>q;q.push_back(1);for(int j=1;j<=m;j++){while(q.size()&&w[i][j]<=w[i][q.back()]) q.pop_back();q.push_back(j);while(q.size()&&q.front()<=j-a) q.pop_front();min1[i][j]=w[i][q.front()];}}memcpy(c,max1,sizeof max1);for(int j=1;j<=m;j++){deque<ll>q;q.push_back(1);for(int i=1;i<=n;i++){while(q.size()&&c[i][j]>=c[q.back()][j]) q.pop_back();q.push_back(i);while(q.size()&&q.front()<=i-a) q.pop_front();max1[i][j]=c[q.front()][j];}}memcpy(c,min1,sizeof min1);for(int j=1;j<=m;j++){deque<ll>q;q.push_back(1);for(int i=1;i<=n;i++){while(q.size()&&c[i][j]<=c[q.back()][j]) q.pop_back();q.push_back(i);while(q.size()&&q.front()<=i-a) q.pop_front();min1[i][j]=c[q.front()][j];}}ll sum=0x3f3f3f3f;for(int i=a;i<=n;i++){for(int j=a;j<=m;j++){sum=min(sum,max1[i][j]-min1[i][j]);}}cout<<sum<<endl;return 0;
}

二维转一维去写 

#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 1010, INF = 1e9;int n, m, k;
int w[N][N];
int row_min[N][N], row_max[N][N];
int q[N];void get_min(int a[], int b[], int tot)
{int hh = 0, tt = -1;for (int i = 1; i <= tot; i ++ ){if (hh <= tt && q[hh] <= i - k) hh ++ ;while (hh <= tt && a[q[tt]] >= a[i]) tt -- ;q[ ++ tt] = i;b[i] = a[q[hh]];}
}void get_max(int a[], int b[], int tot)
{int hh = 0, tt = -1;for (int i = 1; i <= tot; i ++ ){if (hh <= tt && q[hh] <= i - k) hh ++ ;while (hh <= tt && a[q[tt]] <= a[i]) tt -- ;q[ ++ tt] = i;b[i] = a[q[hh]];}
}int main()
{scanf("%d%d%d", &n, &m, &k);for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )scanf("%d", &w[i][j]);for (int i = 1; i <= n; i ++ ){get_min(w[i], row_min[i], m);get_max(w[i], row_max[i], m);}int res = INF;int a[N], b[N], c[N];for (int i = k; i <= m; i ++ ){for (int j = 1; j <= n; j ++ ) a[j] = row_min[j][i];get_min(a, b, n);for (int j = 1; j <= n; j ++ ) a[j] = row_max[j][i];get_max(a, c, n);for (int j = k; j <= n; j ++ ) res = min(res, c[j] - b[j]);}printf("%d\n", res);return 0;
}

蓝桥杯-子矩阵

题目描述

给定一个 n × m （n 行 m 列）的矩阵。

设一个矩阵的价值为其所有数中的最大值和最小值的乘积。求给定矩阵的所有大小为 a × b （a 行 b 列）的子矩阵的价值的和。

答案可能很大，你只需要输出答案对 998244353 取模后的结果。

输入格式

输入的第一行包含四个整数分别表示 n, m, a, b ，相邻整数之间使用一个空格分隔。

接下来 n 行每行包含 m 个整数，相邻整数之间使用一个空格分隔，表示矩阵中的每个数 Ai, j 。

输出格式

输出一行包含一个整数表示答案。

样例输入

2 3 1 2
1 2 3
4 5 6

样例输出

58

提示

1×2+2×3+4×5+5×6 = 58 。

对于 40% 的评测用例，1 ≤ n, m ≤ 100 ；

对于 70% 的评测用例，1 ≤ n, m ≤ 500 ；

对于所有评测用例，1 ≤ a ≤ n ≤ 1000 1 ≤ b ≤ m ≤ 1000 1 ≤ Ai, j ≤ 109 。

暴力O（n*m*a*b) 

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
#include<deque>
using namespace std;
typedef long long ll;
const int N=1e3+10;
ll c[N][N];
int main()
{int n,m,a,b;cin>>n>>m>>a>>b;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++) cin>>c[i][j];ll sum=0;for(int i=1;i+a<=n+1;i++){for(int j=1;j+b<=m+1;j++){ll max1=0,min1=0x3f3f3f3f;for(int x=i;x<i+a;x++){for(int y=j;y<j+b;y++){if(max1<c[x][y]) max1=c[x][y];if(min1>c[x][y]) min1=c[x][y];//	cout<<c[x][y]<<" ";}//cout<<endl;}sum+=(max1*min1)%998244353;sum%=998244353;//	cout<<endl;}}cout<<sum<<endl;return 0;
}

 

#include<iostream>
#include<algorithm>
#include<deque>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=1e3+10;
ll max1[N][N],min1[N][N];
ll w[N][N],c[N][N];
int n,m,a,b;
int main()
{cin>>n>>m>>a>>b;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++) cin>>w[i][j];for(int i=1;i<=n;i++){deque<ll>q;for(int j=1;j<=m;j++){while(q.size()&&w[i][j]>=w[i][q.back()]) q.pop_back();q.push_back(j);while(q.size()&&q.front()<=j-b) q.pop_front();max1[i][j]=w[i][q.front()];}}for(int i=1;i<=n;i++){deque<ll>q;for(int j=1;j<=m;j++){while(q.size()&&w[i][j]<=w[i][q.back()]) q.pop_back();q.push_back(j);while(q.size()&&q.front()<=j-b) q.pop_front();min1[i][j]=w[i][q.front()];}}memcpy(c,max1,sizeof max1);for(int j=1;j<=m;j++){deque<ll>q;for(int i=1;i<=n;i++){while(q.size()&&c[i][j]>=c[q.back()][j]) q.pop_back();q.push_back(i);while(q.size()&&q.front()<=i-a) q.pop_front();max1[i][j]=c[q.front()][j];}}memcpy(c,min1,sizeof min1);for(int j=1;j<=m;j++){deque<ll>q;for(int i=1;i<=n;i++){while(q.size()&&c[i][j]<=c[q.back()][j]) q.pop_back();q.push_back(i);while(q.size()&&q.front()<=i-a) q.pop_front();min1[i][j]=c[q.front()][j];}}ll sum=0;for(int i=a;i<=n;i++){for(int j=b;j<=m;j++){sum=(sum+(min1[i][j]*max1[i][j])% 998244353)%998244353;}}cout<<sum<<endl;return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/543145.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Selenium教程：一文了解Selenium的元素查找

Selenium教程：一文了解Selenium的元素查找

注&#xff1a;本文内容基于selenium 3.141.0 Selenium的元素查找指的是使用Selenium WebDriver库中提供的方法来定位和操作网页上的各种元素&#xff0c;如文本框、按钮、下拉框、链接等。通过元素查找&#xff0c;可以在自动化测试中模拟用户操作&#xff0c;比如输入文本、点…
阅读更多...
C语言 内存函数

C语言 内存函数

目录 前言 一、memcpy()函数 二、memmove()函数 三、memset函数 四、memcmp()函数 总结 前言 在C语言中内存是我们用来存储数据的地址&#xff0c;今天我们来讲一下C语言中常用的内存函数。 一、memcpy()函数 memcpy()函数与我们之前讲的strcpy()函数类似&#xff0c;只…
阅读更多...
分布式调用与高并发处理（二）| Dubbo

分布式调用与高并发处理（二）| Dubbo

文章目录 Dubbo概念_什么是分布式系统单机架构集群架构分布式架构单机、集群和分布式的区别 Dubbo概念_什么是RPCRPC两个作用&#xff1a;常见 RPC 技术和框架&#xff1a; Dubbo概念_简介Dubbo能做什么Dubbo支持的协议 Dubbo概念_核心组件注册中心Registry服务提供者Provider服…
阅读更多...
AI - 决策树模型

AI - 决策树模型

&#x1f914;决策树算法 决策树的思想来源可以追溯到古希腊时期&#xff0c;当时的哲学家们就已经开始使用类似于决策树的图形来表示逻辑推理过程。然而&#xff0c;决策树作为一种科学的决策分析工具&#xff0c;其发展主要发生在20世纪。 在20世纪50年代&#xff0c;美国兰…
阅读更多...
Xinstall助力web唤起iOS，打破平台壁垒，实现无缝跳转

Xinstall助力web唤起iOS，打破平台壁垒，实现无缝跳转

在移动互联网时代&#xff0c;web与App之间的跳转已成为用户日常使用中不可或缺的一部分。然而&#xff0c;对于iOS系统的用户来说&#xff0c;web唤起App的过程往往充满了挑战和不便。这时&#xff0c;Xinstall作为一款专业的移动开发者服务工具&#xff0c;为开发者们提供了解…
阅读更多...
RPC通信原理（一）

RPC通信原理（一）

RPC通信原理 RPC的概念 如果现在我有一个电商项目&#xff0c;用户要查询订单&#xff0c;自然而然是通过Service接口来调用订单的实现类。 我们把用户模块和订单模块都放在一起&#xff0c;打包成一个war包&#xff0c;然后再tomcat上运行&#xff0c;tomcat占有一个进程&am…
阅读更多...
Transformer代码从零解读【Pytorch官方版本】

Transformer代码从零解读【Pytorch官方版本】

文章目录 1、Transformer大致有3大应用2、Transformer的整体结构图3、如何处理batch-size句子长度不一致问题4、MultiHeadAttention&#xff08;多头注意力机制&#xff09;5、前馈神经网络6、Encoder中的输入masked7、完整代码补充知识&#xff1a; 1、Transformer大致有3大应…
阅读更多...
分享一下自己总结的7万多字java面试笔记和一些面试视频，简历啥的，已大厂上岸

分享一下自己总结的7万多字java面试笔记和一些面试视频，简历啥的，已大厂上岸

分享一下自己总结的7万多字java面试笔记和一些面试视频&#xff0c;简历啥的&#xff0c;已大厂上岸 自己总结的面试简历资料&#xff1a;https://pan.quark.cn/s/8b602fe53b58 文章目录 SSMspringspring 的优点&#xff1f;IoC和AOP的理解**Bean 的生命周期****列举一些重要…
阅读更多...
关于工业机器人的四大保养事项

关于工业机器人的四大保养事项

工业机器人的保养周期和注意事项会根据具体机器人的型号、使用环境和工作负荷等因素而有所不同。一般来说&#xff0c;以下是一些常见的保养周期和注意事项&#xff1a; 工业机器人保养注意事项如下&#xff1a; 一、常规保养 1.清洁与除尘&#xff1a;定期清洁机器人的外壳、…
阅读更多...
C#，图论与图算法，双连通图（Biconnected Components of Graph）的算法与源代码

C#，图论与图算法，双连通图（Biconnected Components of Graph）的算法与源代码

1 双连通图（Biconnected Components of Graph） 如果任意两个顶点之间有两条顶点不相交的路径，则无向图称为双连通图。在双连通图中，有一个通过任意两个顶点的简单循环。 按照约定，由边连接的两个节点构成双连通图，但这并不验证上述属性。对于具有两个以上顶点的图，必须…
阅读更多...
音视频如何快速转二维码？在线生成音视频活码的教程

音视频如何快速转二维码？在线生成音视频活码的教程

音频文件的二维码制作步骤是什么样的呢&#xff1f;扫描二维码来展现内容是很流行的一种方式&#xff0c;基本上日常生活中经常会用的图片、音频、视频等都可以使用生成二维码的方式。现在很多的幼儿园或者学校会录制孩子的音频或者视频内容用来展示&#xff0c;那么二维码制作…
阅读更多...
Linux——ELK日志分析系统

Linux——ELK日志分析系统

实验环境 虚拟机三台CentOS 7.9&#xff0c; 组件包 elasticsearch-5.5.0.rpm elasticsearch-head.tar.gz node-v8.2.1.tar.gz phantomjs-2.1.1-linux-x86_64.tar.bz2 logstash-5.5.1.rpm kibana-5.5.1-x86_64.rpm 初始…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023