题目:
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1] 输出:1
示例 3:
输入:nums = [5,4,-1,7,8] 输出:23
详细讲解:
本题接的重点在「关键 1:理解题意」和「关键 2:如何定义子问题(如何定义状态)」和「最后再谈谈「无后效性」。
关键 1:理解题意
题目要我们找出和最大的连续子数组的值是多少,「连续」是关键字,连续很重要,不是子序列。
题目只要求返回结果,不要求得到最大的连续子数组是哪一个。这样的问题通常可以使用「动态规划」解决。
关键 2:如何定义子问题(如何定义状态)
设计状态思路:把不确定的因素确定下来,进而把子问题定义清楚,把子问题定义得简单。动态规划的思想通过解决了一个一个简单的问题,进而把简单的问题的解组成了复杂的问题的解。
友情提示:上面这句话大家姑且这么一看,脑子里有个印象,没有那么绝对。可能不同的人看会有不同的理解。如果我以后讲解的动态规划的设计思想与这里讲解的「设计状态思路」不一样的,我会再和大家说明。如果讲解有误导的地方,还请大家指出。,
我们 不知道和最大的连续子数组一定会选哪一个数,那么我们可以求出 所有 经过输入数组的某一个数的连续子数组的最大和。
例如,示例 1 输入数组是 [-2,1,-3,4,-1,2,1,-5,4] ,我们可以求出以下子问题:
子问题 1:经过 −2-2−2 的连续子数组的最大和是多少;
子问题 2:经过 111 的连续子数组的最大和是多少;
子问题 3:经过 −3-3−3 的连续子数组的最大和是多少;
子问题 4:经过 444 的连续子数组的最大和是多少;
子问题 5:经过 −1-1−1 的连续子数组的最大和是多少;
子问题 6:经过 222 的连续子数组的最大和是多少;
子问题 7:经过 111 的连续子数组的最大和是多少;
子问题 8:经过 −5-5−5 的连续子数组的最大和是多少;
子问题 9:经过 444 的连续子数组的最大和是多少。
一共 9 个子问题,这些子问题之间的联系并没有那么好看出来,这是因为 子问题的描述还有不确定的地方(这件事情叫做「有后效性」,我们在本文的最后会讲解什么是「无后效性」)。
例如「子问题 3」:经过 −3-3−3 的连续子数组的最大和是多少。
「经过 −3-3−3 的连续子数组」我们任意举出几个:
[-2,1,-3,4] ,−3-3−3 是这个连续子数组的第 3 个元素;
[1,-3,4,-1] ,−3-3−3 是这个连续子数组的第 2 个元素;
……
我们不确定的是:−3-3−3 是连续子数组的第几个元素。那么我们就把 −3-3−3 定义成连续子数组的最后一个元素。在新的定义下,我们列出子问题如下:
子问题 1:以 −2-2−2 结尾的连续子数组的最大和是多少;
子问题 2:以 111 结尾的连续子数组的最大和是多少;
子问题 3:以 −3-3−3 结尾的连续子数组的最大和是多少;
子问题 4:以 444 结尾的连续子数组的最大和是多少;
子问题 5:以 −1-1−1 结尾的连续子数组的最大和是多少;
子问题 6:以 222 结尾的连续子数组的最大和是多少;
子问题 7:以 111 结尾的连续子数组的最大和是多少;
子问题 8:以 −5-5−5 结尾的连续子数组的最大和是多少;
子问题 9:以 444 结尾的连续子数组的最大和是多少。
我们加上了「结尾的」,这些子问题之间就有了联系。我们单独看子问题 1 和子问题 2:
子问题 1:以 −2-2−2 结尾的连续子数组的最大和是多少;
以 −2-2−2 结尾的连续子数组是 [-2],因此最大和就是 −2-2−2。
子问题 2:以 111 结尾的连续子数组的最大和是多少;
以 111 结尾的连续子数组有 [-2,1] 和 [1] ,其中 [-2,1] 就是在「子问题 1」的后面加上 1 得到。−2+1=−1<1-2 + 1 = -1 < 1−2+1=−1<1 ,因此「子问题 2」 的答案是 111。
大家发现了吗,如果编号为 i 的子问题的结果是负数或者 000 ,那么编号为 i + 1 的子问题就可以把编号为 i 的子问题的结果舍弃掉(这里 i 为整数,最小值为 1 ,最大值为 8),这是因为:
一个数 a 加上负数的结果比 a 更小;
一个数 a 加上 000 的结果不会比 a 更大;
而子问题的定义必须以一个数结尾,因此如果子问题 i 的结果是负数或者 000,那么子问题 i + 1 的答案就是以 nums[i] 结尾的那个数。
因为我们把子问题定义的更清楚,子问题之间的联系就容易观察到。这是我们定义子问题、定义状态的经验。
接下来我们按照编写动态规划题解的步骤,把「状态定义」「状态转移方程」「初始化」「输出」「是否可以空间优化」全都写出来。
定义状态(定义子问题)
dp[i]:表示以 nums[i] 结尾 的 连续 子数组的最大和。
说明:「结尾」和「连续」是关键字。
状态转移方程(描述子问题之间的联系)
根据状态的定义,由于 nums[i] 一定会被选取,并且以 nums[i] 结尾的连续子数组与以 nums[i - 1] 结尾的连续子数组只相差一个元素 nums[i] 。
假设数组 nums 的值全都严格大于 000,那么一定有 dp[i] = dp[i - 1] + nums[i]。
可是 dp[i - 1] 有可能是负数,于是分类讨论:
如果 dp[i - 1] > 0,那么可以把 nums[i] 直接接在 dp[i - 1] 表示的那个数组的后面,得到和更大的连续子数组;
如果 dp[i - 1] <= 0,那么 nums[i] 加上前面的数 dp[i - 1] 以后值不会变大。于是 dp[i] 「另起炉灶」,此时单独的一个 nums[i] 的值,就是 dp[i]。
以上两种情况的最大值就是 dp[i] 的值,写出如下状态转移方程:
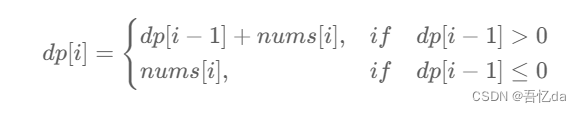
记为「状态转移方程 1」。
状态转移方程还可以这样写,反正求的是最大值,也不用分类讨论了,就这两种情况,取最大即可,因此还可以写出状态转移方程如下:
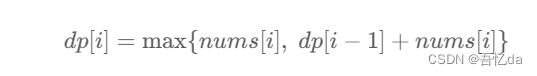
记为「状态转移方程 2」。
友情提示:求解动态规划的问题经常要分类讨论,这是因为动态规划的问题本来就有「最优子结构」的特点,即大问题的最优解通常由小问题的最优解得到。因此我们在设计子问题的时候,就需要把求解出所有子问题的结果,进而选出原问题的最优解。
思考初始值
dp[0] 根据定义,只有 1 个数,一定以 nums[0] 结尾,因此 dp[0] = nums[0]。
思考输出
注意:
这里状态的定义不是题目中的问题的定义,不能直接将最后一个状态返回回去;
这里状态的定义不是题目中的问题的定义,不能直接将最后一个状态返回回去;
这里状态的定义不是题目中的问题的定义,不能直接将最后一个状态返回回去。
重要的事情说三遍,有时候写东西写得多了,怕读者看不到重点,所以会想方设法进行强调,一句话翻来覆去反复说。我以前和一个在新东方当英语老师的朋友交流过,这样的效果最好。大家可以理解为职业病,我们更多是想要照顾到新手朋友们。大佬要是觉得我讲得啰嗦了,还请忽略。
简单的动态规划问题,很有可能问的问题就可以设计成为子问题,复杂的动态规划问题就没有那么容易看出子问题应该如何设计了,这需要一定的解决问题的经验。
这个问题的输出是把所有的 dp[0]、dp[1]、……、dp[n - 1] 都看一遍,取最大值。 同样的情况也适用于「力扣」第 300 题:「最长上升子序列」(以后我们有空,再把这道题拿出来再讲一遍,超级超级重要的一道动态规划问题)。
public class Solution {public int maxSubArray(int[] nums) {int len = nums.length;// dp[i] 表示:以 nums[i] 结尾的连续子数组的最大和int[] dp = new int[len];dp[0] = nums[0];for (int i = 1; i < len; i++) {if (dp[i - 1] > 0) {dp[i] = dp[i - 1] + nums[i];} else {dp[i] = nums[i];}}// 也可以在上面遍历的同时求出 res 的最大值,这里我们为了语义清晰分开写,大家可以自行选择int res = dp[0];for (int i = 1; i < len; i++) {res = Math.max(res, dp[i]);}return res;}
}