构建一元一次方程

100个（X, y ），大概是’y=3x+4’

import numpy as npnp.random.seed(42)  # to make this code example reproducible
m = 100  # number of instances
X = 2 * np.random.rand(m, 1)  # column vector
y = 4 + 3 * X + np.random.randn(m, 1)  # column vector

将坐标可视化

import matplotlib.pyplot as pltplt.figure(figsize=(6, 4))
plt.scatter(X, y, c='b', label='Data points')
plt.xlabel("x")
plt.ylabel("y")
plt.axis([0, 2, 0, 15])
plt.grid()
plt.legend()
plt.show()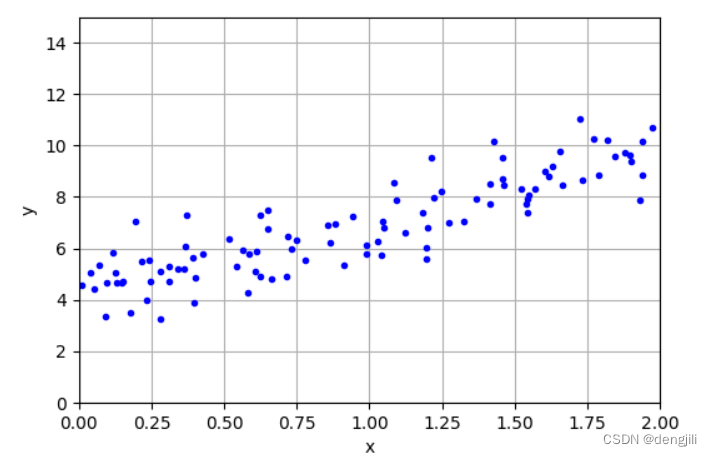

根据做坐标数据，推出函数

矩阵计算，怎么计算的不用管，只需要知道根据坐标就可以计算得出

from sklearn.preprocessing import add_dummy_featureX_b = add_dummy_feature(X)  # add x0 = 1 to each instance
theta_best = np.linalg.inv(X_b.T @ X_b) @ X_b.T @ y

输出

这里有两个参数，对应y=ax+b中的a，b，现在只需要根据横坐标的起始结束0,2就可以画出线性

也是通过上述的矩阵计算

X_new = np.array([[0], [2]])
X_new_b = add_dummy_feature(X_new)  # add x0 = 1 to each instance
y_predict = X_new_b @ theta_best
y_predict

输出

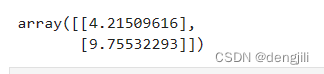
也就是，我们得到两个坐标，（0， 4.21509616），（2， 9.75532293），根据这两个点，我们就可以画出一条线

import matplotlib.pyplot as pltplt.figure(figsize=(6, 4))plt.plot(X_new, y_predict, "r-")
plt.plot(X, y, "b.")plt.xlabel("x")
plt.ylabel("y")
plt.axis([0, 2, 0, 15])
plt.grid()
plt.show()

图中红色的线就是我们根据数据推出来的，也就是通过数据学习到的，然后可以根据红色的线，我们就可以去预测其他的数据了，这就是我们机器学习的过程

简化流程，得到参数ab

直接使用sklearn提供的LinearRegression模型，输入数据就可以得到参数了

from sklearn.linear_model import LinearRegressionlin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.intercept_, lin_reg.coef_

输出

再跟进起始结束，就可以画出线了

X_new = np.array([[0], [2]])
lin_reg.predict(X_new)y_predict = lin_reg.predict(X_new)
y_predict

画图

import matplotlib.pyplot as pltplt.figure(figsize=(6, 4))plt.plot(X_new, y_predict, "r-")
plt.plot(X, y, "b.")plt.xlabel("x")
plt.ylabel("y")
plt.axis([0, 2, 0, 15])
plt.grid()
plt.show()

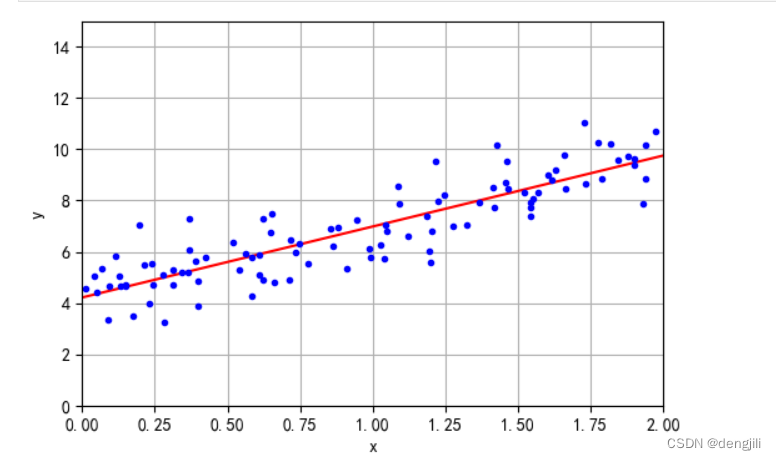
到这里，已经完成了入门